Теория вероятностей. Контрольная работа по дисциплине Теория вероятностей и математическая статистика иразделам теории вероятностей Группа авт241
 Скачать 0.61 Mb. Скачать 0.61 Mb.
|
|
МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ НОВОСИБИРСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСТИЕТ Кафедра вычислительной техники Контрольная работа по дисциплине «Теория вероятностей и математическая статистика» и разделам теории вероятностей Группа: АВТ-241 Студент: Базаров Б.Н. Преподаватель: Пинигина Д. Л. Вариант: 2 Дата сдачи: 12.04.2023 Новосибирск 2023 Задача №1. Условие: Бросают 2 кубика. Представить через элементарные событие, состоящее в выпадении суммы очков больше 6. Найти вероятность этого события. Решение: 1)Если на первом кубике 1, то на втором может выпасть число 6 и их сумма >6. 2)Если на первом кубике 2, то на втором может выпасть любое число (5-6) и их сумма >6. 3)Если на первом кубике 3, то на втором может выпасть любое число (4-6) и их сумма >6. 4)Если на первом кубике 4, то на втором может выпасть (3-6) и их сумма >6. 5)Если на первом кубике 5, то на втором может выпасть (2-6) и их сумма >6. 6)Если на первом кубике 6, то на втором может выпасть (1-6) и их сумма >6. Значит событие А = 1*1+1*2+1*3+1*4+1*5+1*6=21 Тогда вероятность выпадения события Р(А) = 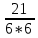 = 0,583 = 0,583Ответ: 0.583 Задача №2. Условие: Вероятность отсутствия одного депутата горсовета на заседании равна 0,1. Найти вероятность того, что из 12 депутатов будет 2 отсутствовать. Определить наивероятнейшее число отсутствующих среди 12 и найти его вероятность. Решение: Событие А = отсутствие 1 депутата Вероятность Р(А) = 0.1 Формула Бернулли: 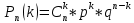 n = 12 k = 2 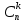 – число сочетаний без повторений – число сочетаний без повторений 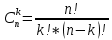 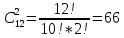 p = 0.1 q = 0.9 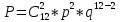 = 0,230128 = 0,230128Наивероятнейшее число отсутствующих лежит в промежутке 𝑛𝑝−𝑞≤𝑘≤𝑛𝑝+𝑝 12*0.1-0.9≤k≤12*0.1+0.9 => 0.3≤k≤2.1 => k=2 Значит наивероятнейшее число отсутствующих это 2 депутата, а вероятность этого события уже найдена и равна 0.230128 Ответ: Р(А) = 0.230128, k = 2, P(отсутствие 2-х депутатов) = Р(А) = 0.230128 Задача №3. Условие: Вся продукция цеха проверяется тремя контролерами, причем контролер проверяет 35% изделий, второй – 30%, третий – 35%. Вероятность того, что первый контролер пропустит брак, равна 0,01, второй – 0,02, третий – 0,03. Взятое наудачу изделие, маркированное как стандартное, оказалось бракованным. Найти вероятность того, что это изделие проверялось вторым контролером. Решение: Количество проверяемой продукции контроллерами: Первым – 35% Вторым – 30% Третьим – 35% Вероятность пропуска брака на контролере: На первом – 0.01 На втором – 0.02 На третьем – 0.03 Необходимо найти вероятность того, что второй контролер пропустил данное бракованное изделие Количество изделий, проходящее через первый контролер – 0.35 от общего, а количество пропущенных бракованных изделий через первый контроллер – 0.35*0.01 = 0.0035 от общего количества. Точно также для второго контролера количество пропущенных бракованных изделий – 0.30*0.02 = 0.006 от общего количества. И для третьего количество пропущенных бракованных изделий – 0.35*0.03 = 0.0105 от общего количества. Общее количество пропущенной бракованной продукции: 0,0035+0,006+0,0105=0,02 Тогда вероятность что ошибку выдаст второй контролер: Р = 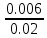 =0.3 =0.3Ответ: 0.3 Задача №4. Условие: Найти вероятность выигрыша в лотерее «5 из 15». Решение: Для выигрыша в лотерее игроку необходимо угадать 5 из 15 чисел Тогда вероятность выигрыша: Р= 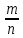 , где m = 1, т. е. есть только 1 вариант выигрыша, а n = , где m = 1, т. е. есть только 1 вариант выигрыша, а n = 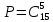 P = 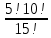 = = 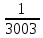 Ответ: 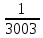 Задача №5. Условие: Случайная величина распределена равномерно (a=-4; b=6). Найти f(x), F(x), Мо, MX, DX. Построить графики f(x), F(x). Дано: a = -4 b = 6 Решение: Модой являются все числа отрезка [-4;6]. Так как распределение равномерное, то плотность постоянна на отрезке: 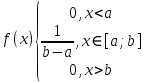 A функция распределения: 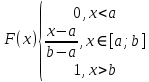 Подставим данные из условия: 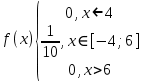 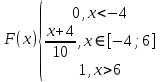 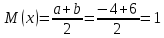 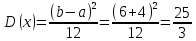 Mo= 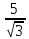 =2,89 =2,89График плотности: 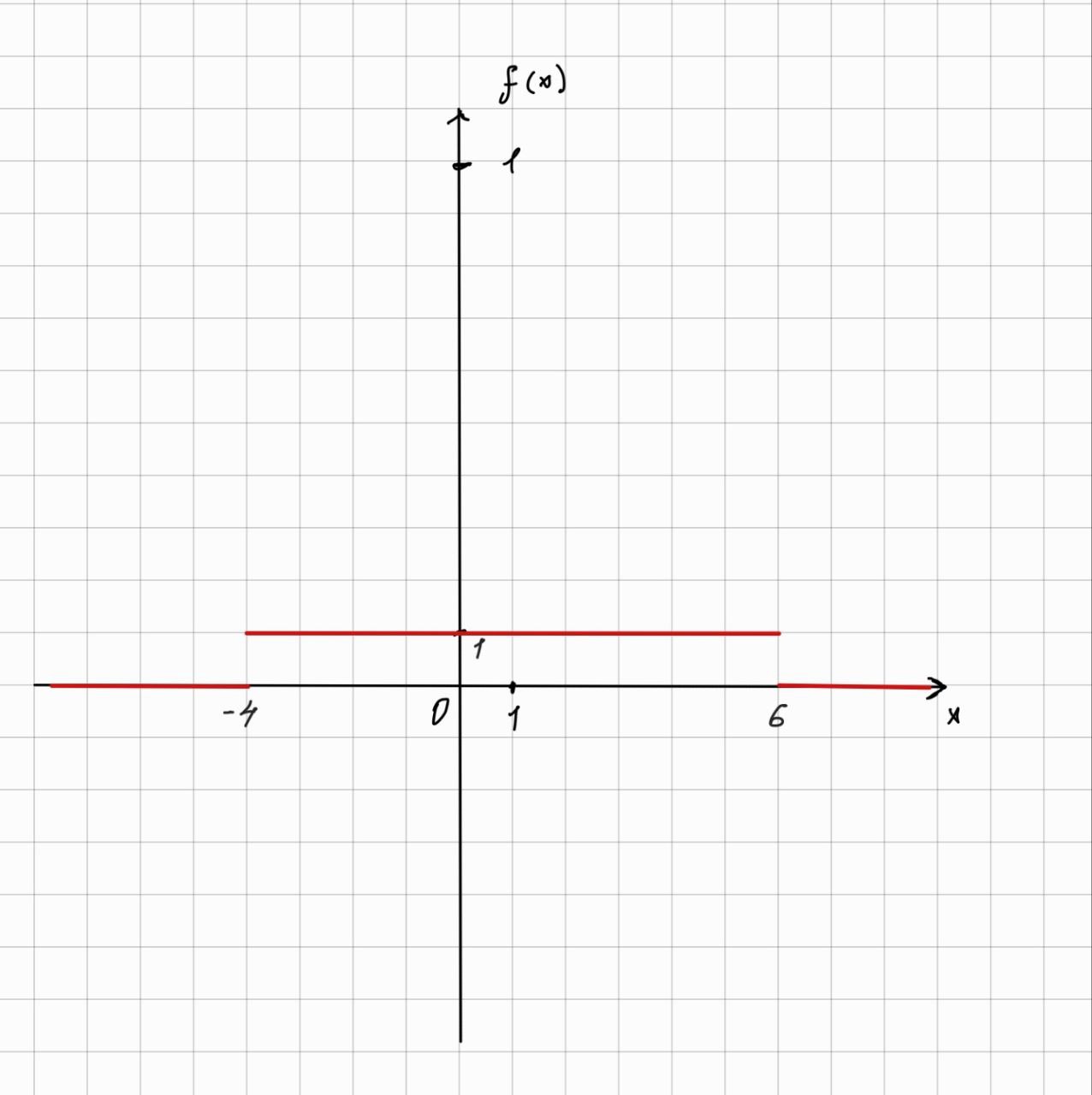 График функции распределения: 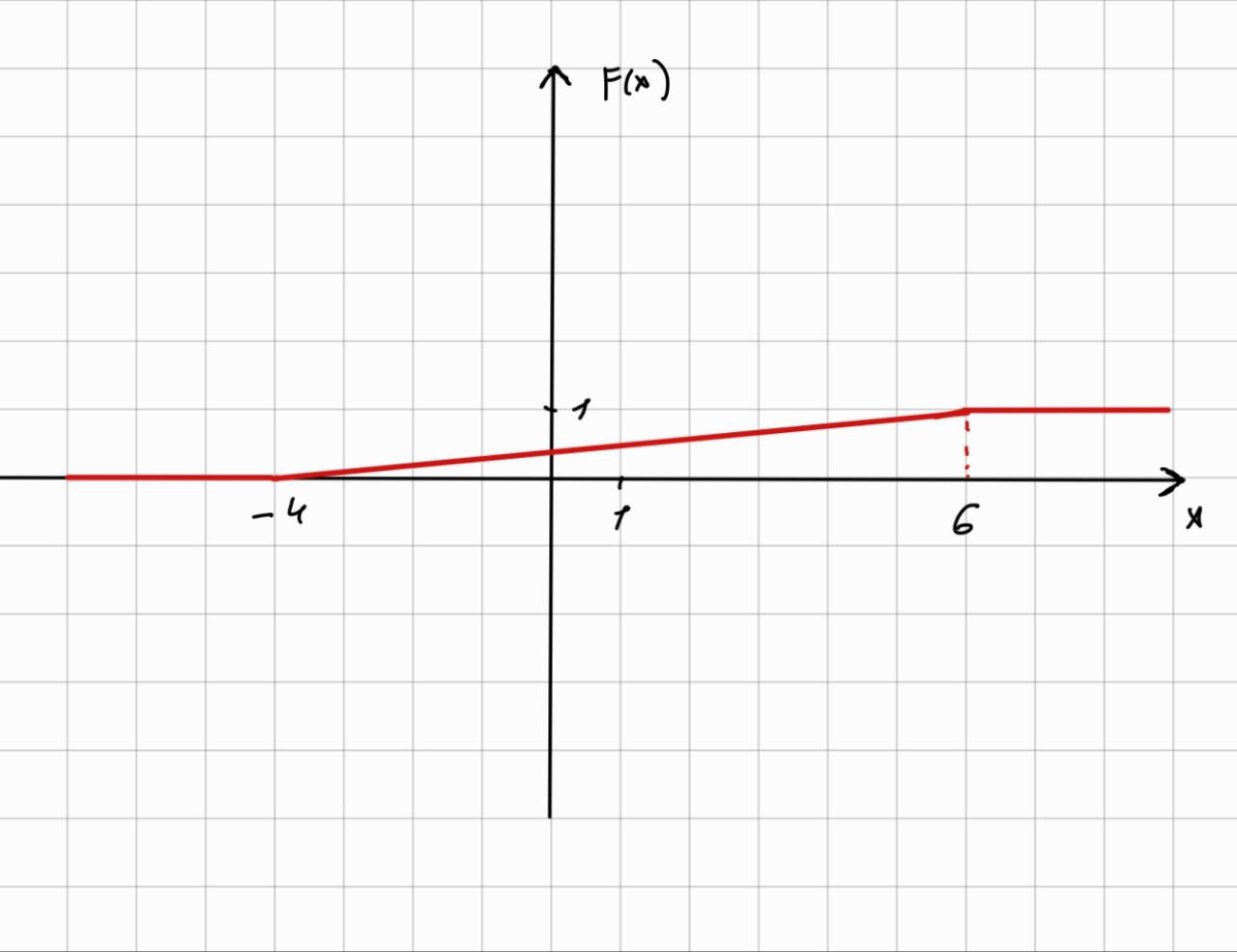  Ответ: 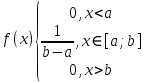 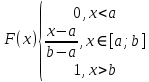 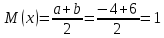 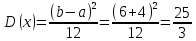 Mo= 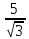 =2,89 =2,89Задача №6. Условие: Случайная величина распределена по биномиальному закону (n=4 ; p= 0,1). Построить полигон, F(x), найти MX, DX, M(1-3X), D(1-3X). Дано: n = 4 p = 0.1 Решение: X распределена по биноминальному закону с параметрами n = 4, p = 0.2 Распределение происходит по закону Бернулли: 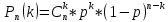 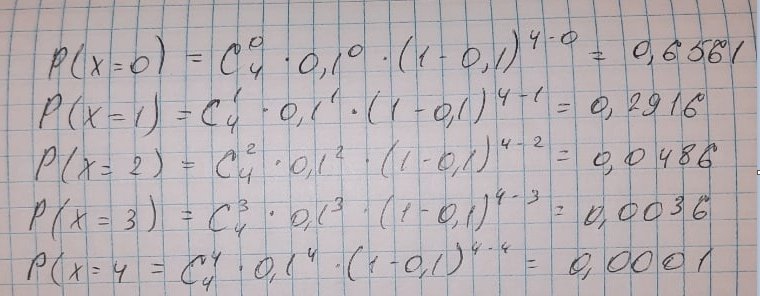
Полигон:   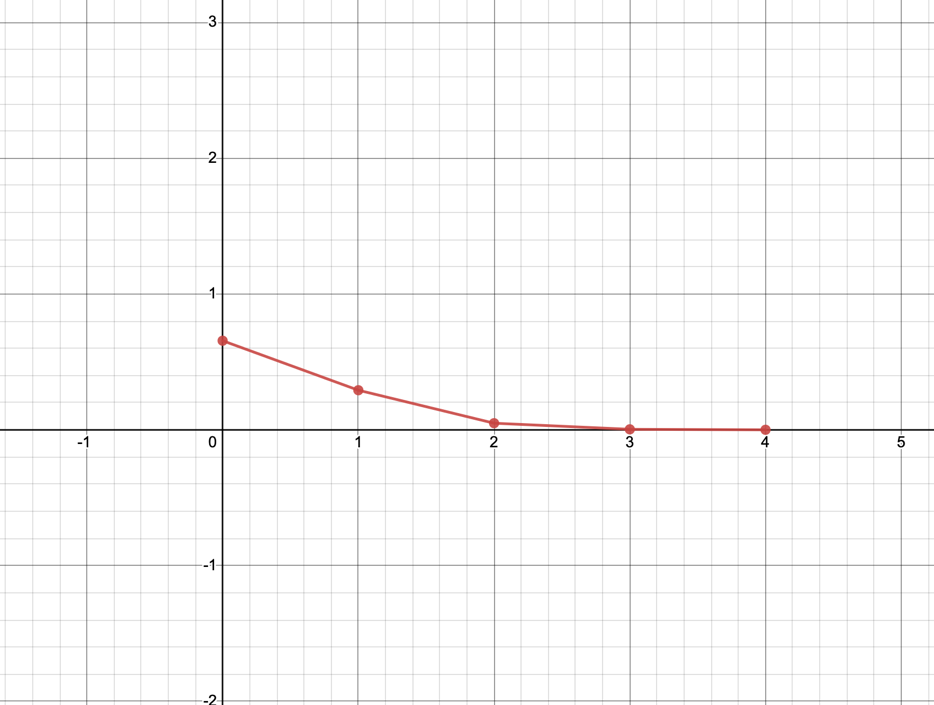   F(x): при 𝑥≤0: 𝐹(𝑥)=0 при 0<𝑥≤1: 𝐹(𝑥)= 0,6561 при 1<𝑥≤2: 𝐹(𝑥)= 0,6561+0,2916=0,9477 при 2<𝑥≤3: 𝐹(𝑥)= 0,9477+0,0486=0,9963 при 3<𝑥<4: 𝐹(𝑥)=0,9963+0,0036=0.9999 при x>4: F(x)=1 (так как это максимальное значение случайной величины) 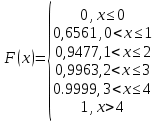 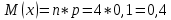 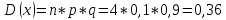 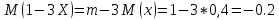 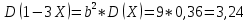 Ответ:M(x)=0,4; D(x)=0,36; M(1-3X)=-0,2; D(1-3X)=3,24. Задача №7. Условие: Задана СВ Х с распределением 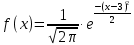 . Найти D(2-3X). . Найти D(2-3X).Решение: Т.к. случайная величина 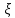 имеет плотность распределения имеет плотность распределения 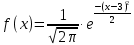 , то , то 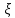 имеет нормальное распределение имеет нормальное распределение 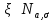 c параметрами c параметрами 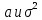 , где по нормальному закону распределения (закон Гаусса) : , где по нормальному закону распределения (закон Гаусса) :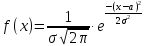 Следует, что M(x) = a = 3, D(x) = 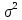 = 1; = 1;Тогда дисперсия D(X) равна параметру 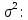 D(X)= D(X)=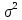 D(X)= 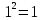 D(2-3X) = 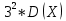 = 9 = 9Ответ:D(2-3X) = 9 |