Вычислительная математика. ВычМатЕрхов8044. Контрольная работа по дисциплине Теория вероятностей и математическая статистика Вариант 4 ст гр. 8044 Ерхов А. Ю
 Скачать 80.83 Kb. Скачать 80.83 Kb.
|
|
МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ Федеральное государственное бюджетное образовательное учреждение высшего образования «Рязанский государственный радиотехнический университет» Кафедра вычислительной и прикладной математики Контрольная работа по дисциплине: «Теория вероятностей и математическая статистика» Вариант 4 Выполнил: ст. гр. 8044 Ерхов А.Ю. Проверил: доцент каф. ВПМ, к.т.н. Проказникова Е.Н. Рязань, 2021 Вариант 4 Дана выборка: 6;8;3;3;7;8;6;5;9;2;2;4;8;5;9;2;5;9;2;2;4;2;8;8;6 По результатам обследования выборки определить: а) величину, которую следует принять за среднюю генеральной совокупности; б) величину, которую следует принять за дисперсию генеральной совокупности; в) доверительный интервал для генеральной средней, если доверительная вероятность В = 0,95. Выборка значений случайной величины: Решение. А) За оценку средней генеральной совокупности принимают среднее выборочное значение: 5.32 Б) За оценку дисперсии обычно принимают исправленную Дисперсию: 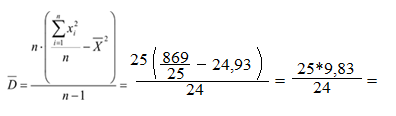 = 10.2395 = 10.2395 В) Для построения интервальной оценки найдем оценку среднего квадратичного отклонения: А оценка среднего квадратичного отклонения для Х меньше в Сп . Коэффициент, необходимый для построения доверительного интервала, в предположении, что мы имеем дело с распределением Стьюдента, зависит от числа степеней свободы (в нашем случае п- 1=24) и от заданной доверительной вероятности 0.95. По соответствующим таблицам можно найти его значение, что в нашем случае составляет 2064, т.о. с вероятностью 0.95 генеральное среднее будет в пределах: 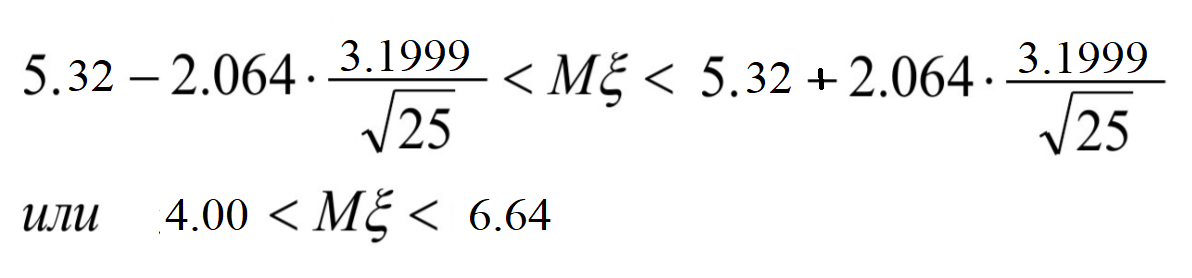 |
