Теория вероятности. Контрольная работа по дисциплине Теория вероятностей и математическая статистика
 Скачать 22.57 Kb.
|
|
Министерство цифрового развития, связи и массовых коммуникаций Российской Федерации Сибирский государственный университет Телекоммуникаций и Информатики Межрегиональный центр переподготовки специалистов КОНТРОЛЬНАЯ РАБОТА по дисциплине «Теория вероятностей и математическая статистика» Работу выполнила студентка 1 курса группы КИТ-22 Вылегжанина Т.О. Работу проверил: Храмова Т.В. Новосибирск 2023 Вариант 1 Задание 1. Комбинаторика Сколько 4-х буквенных слов можно составить из букв слова КАРП? Решение: Переставить буквы в слове можно 4! способами. 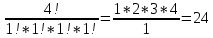 Ответ: 24 слова Задание 2. Основные теоремы Спортсмен попадает в основной состав команды с вероятностью 0,6, а в запас – с вероятностью 0,4. Спортсмен из основного состава команды участвует в соревновании с вероятностью 0,9, из запаса – с вероятностью 0,2. Найти вероятность участия соревновании произвольно выбранного спортсмена. Решение: 1. Гипотезы: А – спортсмен из основного состава команды; В – из запаса; Р(А)=0,6; Р(В)=0,4. 2. Событие С – спортсмен участвует в соревнованиях: Р(С|А)=0,9; Р(С|В)=0,2. 3. Полная вероятность события С: Р(С)=Р(А)*Р(С|А)+Р(В)*Р(С|В); Р(С)=0,6*0,9+0,4*0,2=0,54+0,08=0,62. Ответ: Вероятность участия соревновании произвольно выбранного спортсмена = 0,62. Задание 3. Случайные величины. Найти математическое ожидание, дисперсию и среднее квадратическое отклонение дискретной случайной величины, заданной рядом распределения 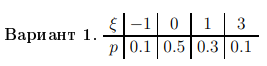 Решение. Запишем формулу для вычисления математического ожидания и подставим в неё данные задачи: 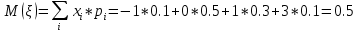 Запишем формулу для вычисления дисперсии и подставим в неё данные задачи:  Среднее квадратическое отклонение вычисляется по формуле: 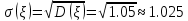 Ответ: 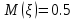 ,  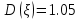,  Задание 4. Нормальное распределение случайной величины Случайная величина распределена по нормальному закону с параметрами a = 10,  = 2. Найдите вероятность того, что случайная величина принимает значения из интервала [7; 12].Решение. Вероятность попадания нормально распределённой величины в интервал вычисляется по формуле: 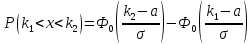 где Ф0(x) - функция Лапласа, её значения можно найти в таблице в конце любого учебника по теории вероятностей. Согласно условиям задачи, имеем  в таблице находим значение Ф0(1)=0.3413;  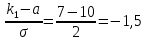 в таблице находим значение Фo(1,5) = 0,4332; с учётом того, что функция Лапласа нечётная, получаем Фo (-1) = - 0,4332; подставим в формулу: 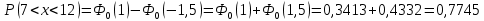 Ответ: 0,7745. |