Законы распределения случайных величин. Законы+распределения+случайных+величин. Решение Для дискретной случайной величины 1 По условию нормировки поэтому
 Скачать 71.29 Kb. Скачать 71.29 Kb.
|
|
Законы распределения случайных величин Задание 1 Для данного закона распределения дискретной случайной величины Х найти: 1) неизвестную вероятность рi ; 2) математическое ожидание; 3) дисперсию; 4) среднее квадратическое отклонение. Построить многоугольник распределения.
Решение Для дискретной случайной величины 1) По условию нормировки 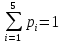 поэтому 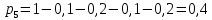 2) Математическое ожидание 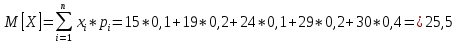 3) Дисперсия 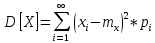  4) Среднее квадратическое отклонение 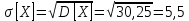  Стоим многоугольник распределения Стоим многоугольник распределенияpx    0.4 0.4      0.2 0.2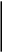   0.1 0.1 15 19 24 29 30 X Ответ: 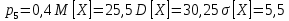 Задание 2 Случайная величина Х задана функцией распределения F(x). Найти: 1) плотность распределения вероятностей; 2) математическое ожидание и дисперсию НСВ Х; 3) вероятности попадания случайной величины в указанные интервалы. Построить графики функции распределения вероятностей и плотности распределения. 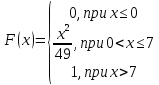 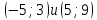 Решение 1) Плотность распределения вероятностей 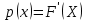 Таким образом 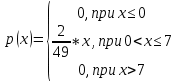 2) Найдем математическое ожидание и дисперсию НСВ Х 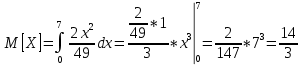 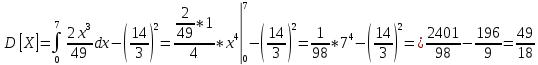 3) Вероятность попадания НСВ в интервал 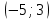 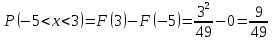 Вероятность попадания НСВ в интервал 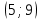 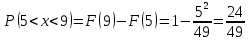   Далее строим графики функции распределения вероятностей и плотности распределения вероятностей Далее строим графики функции распределения вероятностей и плотности распределения вероятностей F(X) p(x) F(X) p(x)   2/7 2/7   1 1     0 7 X 0 7 x 0 7 X 0 7 xОтвет: 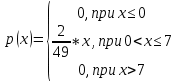 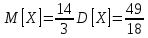 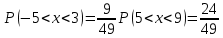 Задание 3 Рыболов ловит рыбу в пруду. Масса пойманной рыбы является нормально распределенной случайной величиной Х с математическим ожиданием а и средним квадратическим отклонением σ. Найти вероятности того, что масса одной пойманной рыбы: 1) находится в пределах от α до β; 2) отклоняется от средней массы не более, чем на δ. а = 450 г, σ = 25 г, α = 425 г, β = 470 г, δ = 30 г. Решение: 1) Так как распределение нормальное, то  следовательно 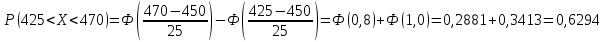 2) Вероятность попадания случайной величины, распределенной по нормальному закону, на интервал, симметричный относительно среднего значения равна 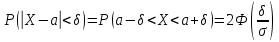 Таким образом 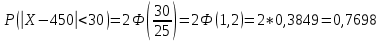 Задание 4 Задача № 21 Чудесенко В.Ф. Сборник заданий по специальным курсам высшей математики (ТР). М.: Высш. школа, 1983. Дана плотность распределения f(x) случайной величины ξ. Найти параметр γ, математическое ожидание Mξ , дисперсию Dξ, функцию распределения случайной величины ξ, вероятность выполнения равенства x1 < ξ < x2. 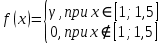 Решение: 1) Для нахождения параметра γ воспользуемся свойством плотности распределения: 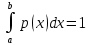  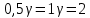 Плотность распределения принимает вид: Плотность распределения принимает вид: 2) Найдем Mξ по формуле 2) Найдем Mξ по формуле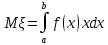 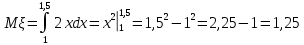 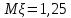 3) Найдем 3) Найдем 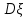 по формуле по формуле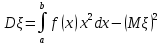 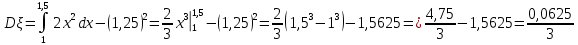 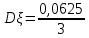 4) Найдем функцию распределения случайной величины ξ. Воспользуемся формулой 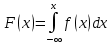 a) Пусть x ≤ 1, 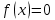  б) Пусть 1,5 ≤ x ≤ 1, 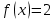 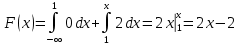 в) Пусть x > 1,5, 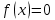 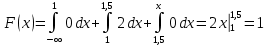 Следовательно, функция распределения имеет вид 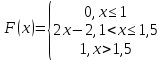 5) Найдем вероятность выполнения неравенства 0 < ξ < 0,5 Воспользуемся формулой 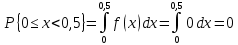 Ответ: 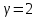 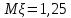 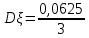 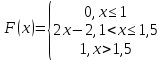  Задание 5 Задача № 22 Чудесенко В.Ф. Сборник заданий по специальным курсам высшей математики (ТР). М.: Высш. школа, 1983. Плотность распределения вероятностей случайной величины ξ имеет вид f (x) = 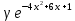 . Найти параметр γ, математическое ожидание Mξ , дисперсию Dξ, функцию распределения случайной величины ξ, вероятность выполнения равенства 0 < ξ < 3/4. . Найти параметр γ, математическое ожидание Mξ , дисперсию Dξ, функцию распределения случайной величины ξ, вероятность выполнения равенства 0 < ξ < 3/4. Решение: 1) Для нахождения параметра γ воспользуемся свойством плотности распределения: 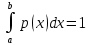  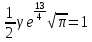 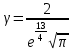 Плотность распределения принимает вид 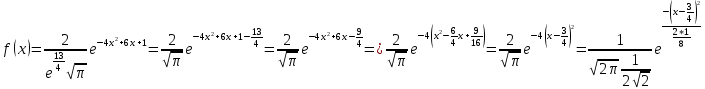 Это нормальное распределение с параметрами 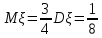 Найдем функцию распределения случайной величины ξ. Воспользуемся формулой 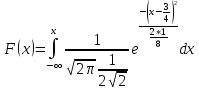 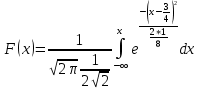 5) Найдем вероятность выполнения неравенства 0 < ξ < ¾ Воспользуемся формулой 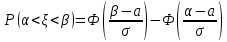 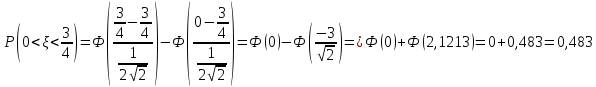 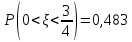 Ответ: 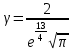 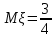 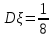 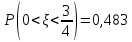 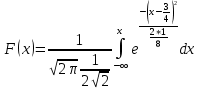 |
