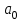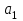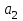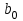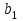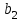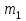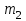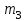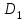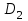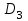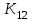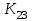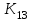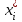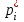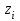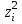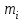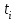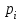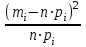Случайные величины НЕТУ. Задача 7 Условие
 Скачать 262.79 Kb. Скачать 262.79 Kb.
|
|
Вариант №6 Задача 7 Условие: Вероятность выигрыша по одному билету лотереи равна 1/6. Случайная величина X – число выигрышных билетов среди четырех купленных. Построить ряд распределения, многоугольник распределения. Найти функцию распределения и построить ее график. Вычислить числовые характеристики: математическое ожидание, дисперсию, среднеквадратическое отклонение. Решение: Пусть p = 1/6 – вероятность выигрыша по одному билету лотереи равна, q = 1 – p = 1 – 1/6 = 5/6 – вероятность проигрыша. Используем формулу Бернулли: 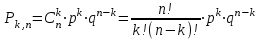 – вероятность того, что событие наступит ровно k раз в n независимых испытаниях. – вероятность того, что событие наступит ровно k раз в n независимых испытаниях.Тогда получим ряд распределения: 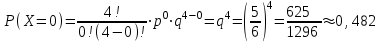 , ,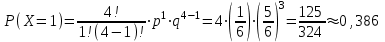 , ,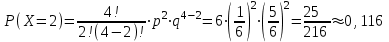 , ,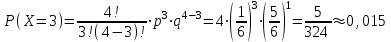 , ,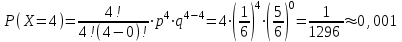 . .или
Многоугольник распределения: 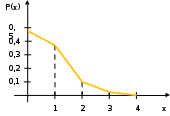 Вычислим функцию распределения 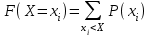
И построим ее график 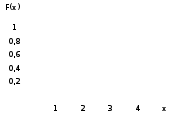 Математическое ожидание 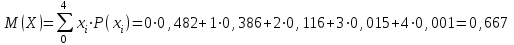 Дисперсия Дисперсия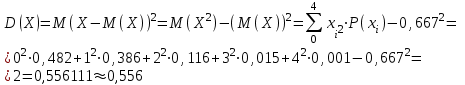 Среднеквадратическое отклонение 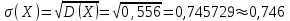 Задача 8 Условие: Задана непрерывная случайная величина X своей плотностью распределения вероятности: 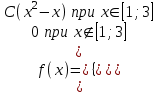 Требуется: определить коэффициент C; найти функцию распределения F(x) схематично построить графики функций f(x) и F(x); вычислить M(X), D(X); определить 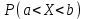 , a = 2, b = 4. , a = 2, b = 4.Решение: Вычислим константу С, исходя из условия нормировки 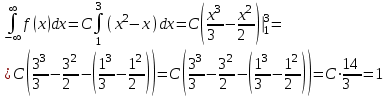 Получаем 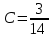 . .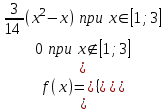 Теперь найдем функцию распределения: 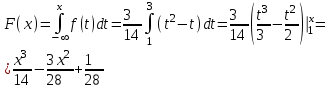 Построим графики f(x) и F(x) 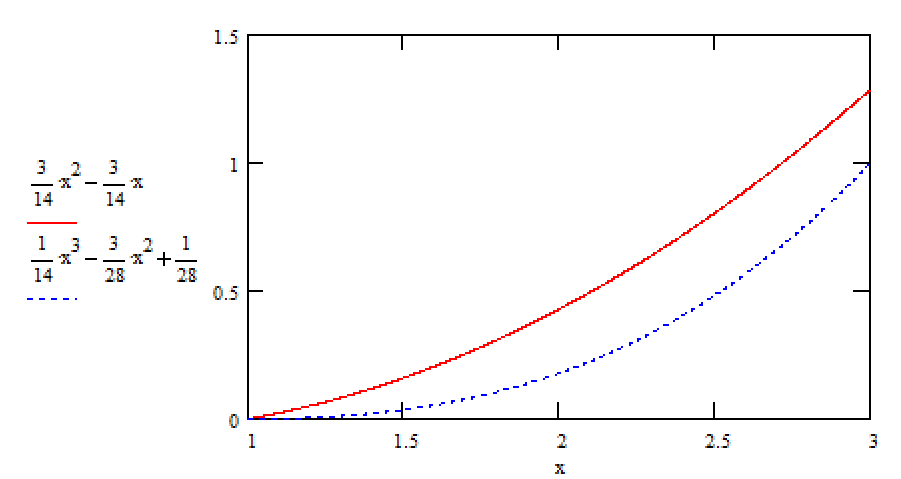 Математическое ожидание 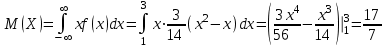 Дисперсия 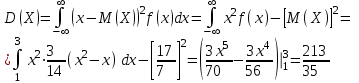 Среднеквадратическое отклонение 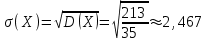 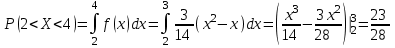 Задача 9 Условие: Двумерный случайный вектор (X, Y) равномерно распределен внутри выделенной жирными прямыми линиями на рисунке области B. Двумерная плотность вероятности f(x,y) одинакова для любой точки этой области B: 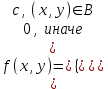 Вычислить коэффициент корреляции между величинами X и Y
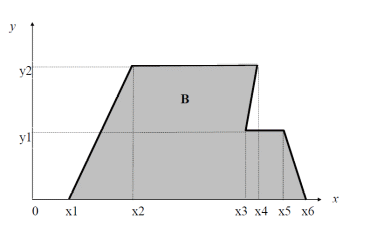 Решение: Построим область B согласно координатам из таблицы и по рисунку выше. 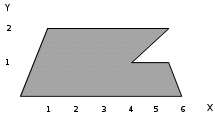 Область B на промежутке 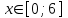 ограничена прямыми: ограничена прямыми: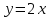 ; ;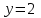 ; ;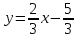 ; ;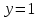 ; ;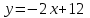 Следовательно, совместная плотность вероятности примет вид: 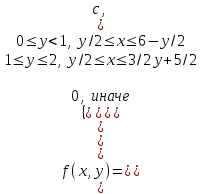 Найдем константу с из условия нормировки: 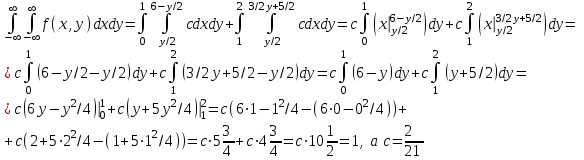 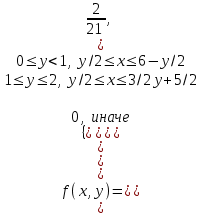 Проверим полученный результат геометрически. Объём тела, ограниченного поверхностью распределения В и плоскостью xOy равен 1, т.е: 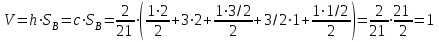 Следовательно, константа  рассчитана верно. рассчитана верно.Вычислим математические ожидания: 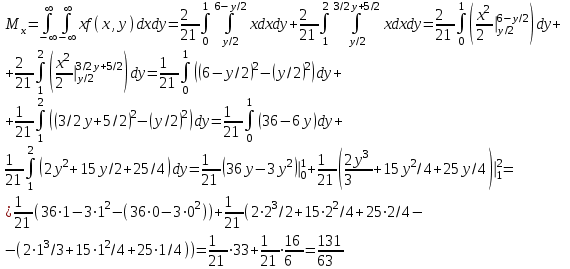 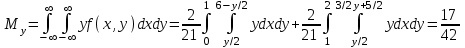 Вычислим дисперсии: 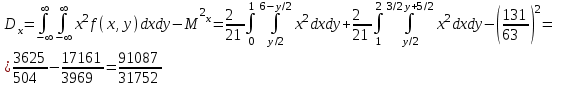 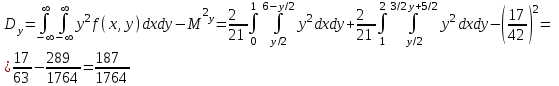 Вычислим корреляционный момент 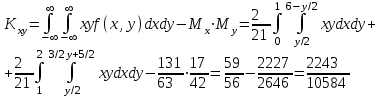 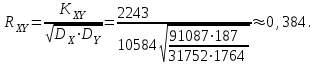 Задача 10 Условие: Задан закон распределения двумерной случайной величины (X, Y).
Задан закон распределения двумерной случайной величины (X, Y). Найти коэффициенты ковариации и корреляции, законы распределения составляющих X и Y. Вычислить математическое ожидание, дисперсию, ско СВ X и СВ Y, корреляционный момент и коэффициент корреляции. Решение: Найдем законы распределения СВ X и СВ Y, суммируя вероятности соответственно по строкам и по столбцам.
Для СВ X: Математическое ожидание 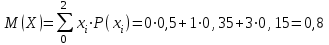 Дисперсия 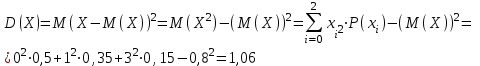 Среднеквадратическое отклонение 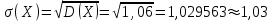 Для СВ Y: Математическое ожидание 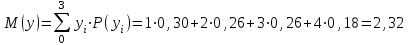 Дисперсия 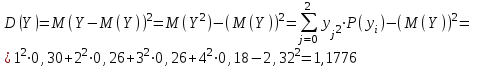 Среднеквадратическое отклонение 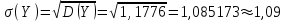 Для СВ X и СВ Y: Ковариация: 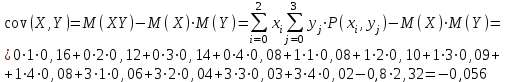 Коэффициент корреляции: 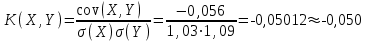 Значение K(X,Y) почти равно 0, поэтому следует сделать вывод об очень слабой отрицательной связи X и Y или практически их некоррелируемости. Задача 10 Условие: Вычислить математическое ожидание и дисперсию величин U и V, а так же определить их коэффициент корреляции 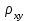 : : 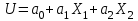 , , 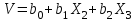 . Конкретные значения коэффициентов . Конкретные значения коэффициентов 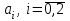 , , 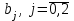 и числовые характеристики случайных величин и числовые характеристики случайных величин 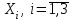 заданы в таблице. заданы в таблице.
Решение: Математические ожидания: 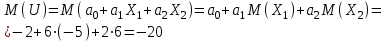 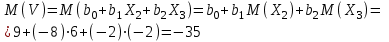 Дисперсии: 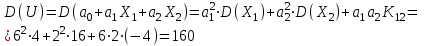 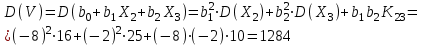 Ковариация: 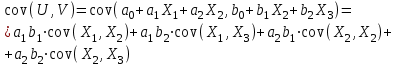 Учитывая, что 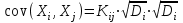 , , 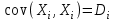 , получаем: , получаем: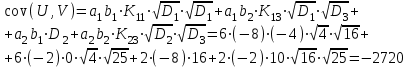 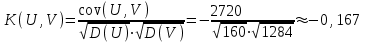 Значение K(U,V) свидетельствует о слабой отрицательной связи U и V. Задача 11 Условие: Дана выборка из генеральной совокупности случайной величины X.
Требуется: составить интервальный статистический ряд; построить гистограмму относительных частот; перейти к дискретному вариационному ряду, взяв за варианты середины частичных интервалов, и построить полигон относительных частот; построить формулу и график эмпирического распределения; вычислить точечные статистические математического ожидания и дисперсии генеральной совокупности; выдвинуть гипотезу о законе распределения случайной величины X, проверить эту гипотезу по критерию Пирсона (на уровне значимости 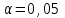 ). ).Найти доверительные интервалы для математического ожидания и дисперсии (доверительную вероятность выбрать самостоятельно). Решение: Построим интервальный статистический ряд. Найдем среди значений признака 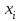 минимальное и максимальное: минимальное и максимальное: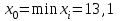 , ,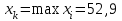 . .Размах выборки: 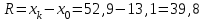 . .Количество интервалов: 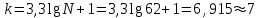 Вычислим возможную длину интервала 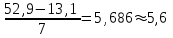 Примем 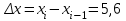 и проведем разбиение на интервалы. Определим количество значений и проведем разбиение на интервалы. Определим количество значений 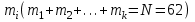 , приходящихся на каждый i-й интервал, и заполним таблицу. , приходящихся на каждый i-й интервал, и заполним таблицу. Перейдем к дискретному вариационному ряду, взяв за варианты середины частичных интервалов. В таблице 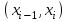 - границы i-го интервала, - границы i-го интервала, 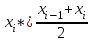 – середина i-го интервала, – середина i-го интервала, 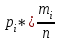 – частота в i-м интервале. – частота в i-м интервале.
Построим теперь полигон относительных частот (рисунок ниже) 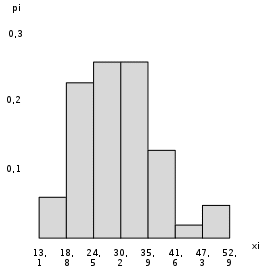 Далее построим формулу и график эмпирического распределения:  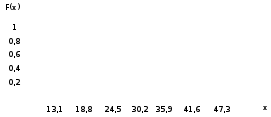 Вычислим точечные статистические математического ожидания и дисперсии генеральной совокупности. Обозначим: 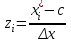 , ,где 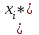 − среднее значение признака в i-ом интервале; − среднее значение признака в i-ом интервале; с− среднее значение признака в интервале с наибольшей частотой, принятое в качестве "нуля"; 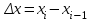 – ширина интервала. – ширина интервала. Для нашей задачи 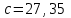 и и 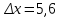 . .Далее рассчитаем 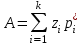 , ,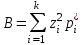 , ,и занесем их в таблицу.
Выборочная средняя: 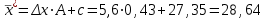 . .Выборочная дисперсия: 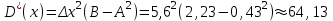 . .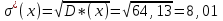 . .Выдвинем гипотезу о нормальном законе распределения случайной величины X и проверим эту гипотезу по критерию Пирсона - 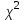 (на уровне значимости (на уровне значимости 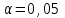 ). ).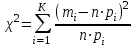 , ,где 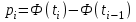 , ,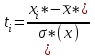 Для статистического ряда определим меру расхождения, сводя результаты расчетов в таблицу. Таблица 4 – Оценка меры расхождения
Вычислив, найдем число "степеней свободы" распределения 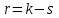 , где k − число интервалов, а s − число связей, накладываемых на частоты. При гипотезе о нормальном распределении число связей равно 3, тогда , где k − число интервалов, а s − число связей, накладываемых на частоты. При гипотезе о нормальном распределении число связей равно 3, тогда 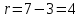 . . На уровне значимости 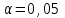 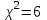 по таблице. Поскольку расчетное значение = 10,38 больше, делаем вывод, что гипотеза об нормальном распределении не соответствует расчетным данным. по таблице. Поскольку расчетное значение = 10,38 больше, делаем вывод, что гипотеза об нормальном распределении не соответствует расчетным данным. . Доверительный интервал для математического ожидания при известной дисперсии, 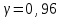 и t = 2,06 определяется по формуле: и t = 2,06 определяется по формуле: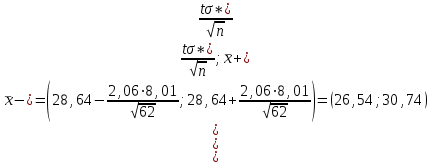 Доверительный интервал для дисперсии определим при 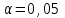 по формуле: по формуле: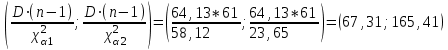 . .Очевидная неточность в определении связана с тем, что случайная величина X все же не распределена по нормальному закону. |