ТЕст. БГУИР. Решение. Радиус сходимости степенного ряда можно найти по формуле Т. к и, то
 Скачать 0.57 Mb.
|
|
2_1. Для степенного ряда  укажите область сходимости.Решение. Радиус сходимости степенного ряда можно найти по формуле:  . Т.к. 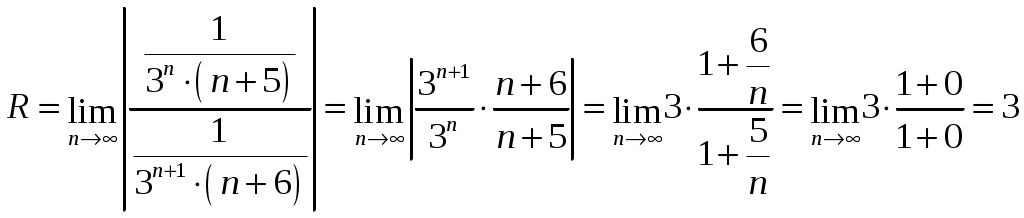 и  , то .Итак, радиус сходимости ряда 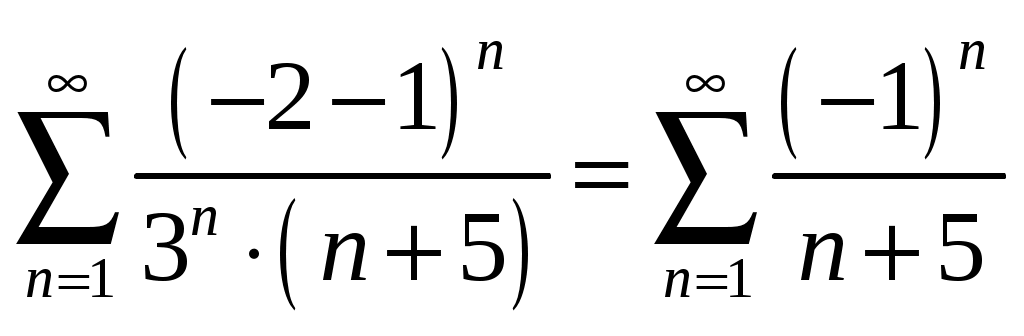 . Определим интервал сходимости данного степенного ряда: .Т.о.,  – интервал сходимости степенного ряда. Исследуем сходимость ряда на концах интервала сходимости.Пусть  . Подставим в заданный степенной ряд и получим знакочередующийся ряд .Для членов полученного ряда выполняются условия:  и  .В соответствии с признаком Лейбница данный ряд сходится и п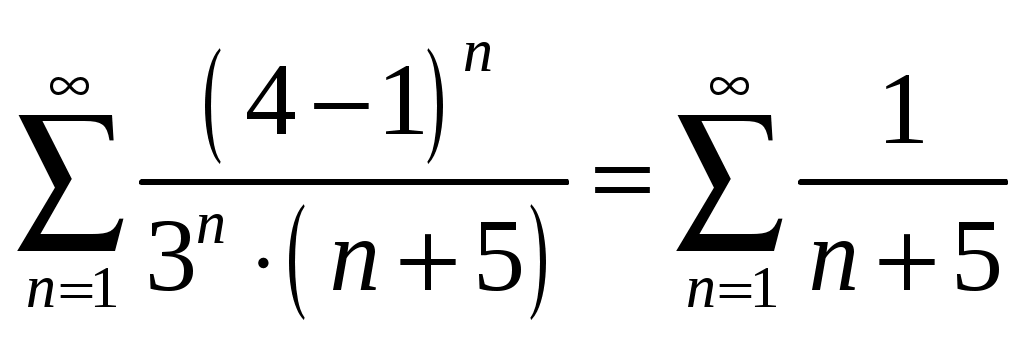ринадлежит области сходимости степенного ряда.Пусть  . Подставим в заданный степенной ряд и получим числовой ряд с положительными членами: . Воспользуемся предельным признаком сравнения. Сравним ряд  с расх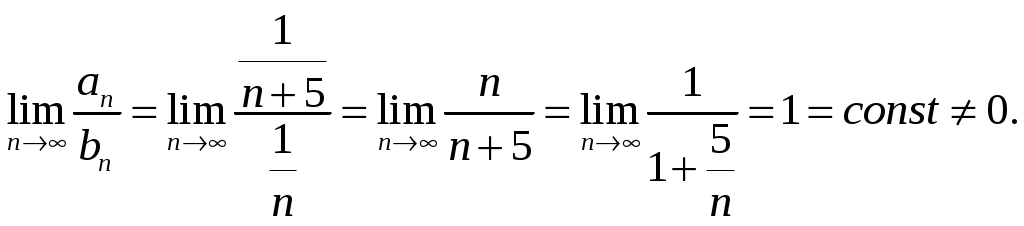одящимся гармоническим рядом  .Тогда:  ,  . Значит, ряд также расходится и принадлежит области сходимости степенного ряда. Итак, областью сходимости данного степенного ряда является промежуток  .Ответ: 3_1. Ряд Фурье функции  Решение. Разложение функции  на интервале  в ряд Фурье имеет вид: . , , .Находим коэффициенты ряда Фурье:   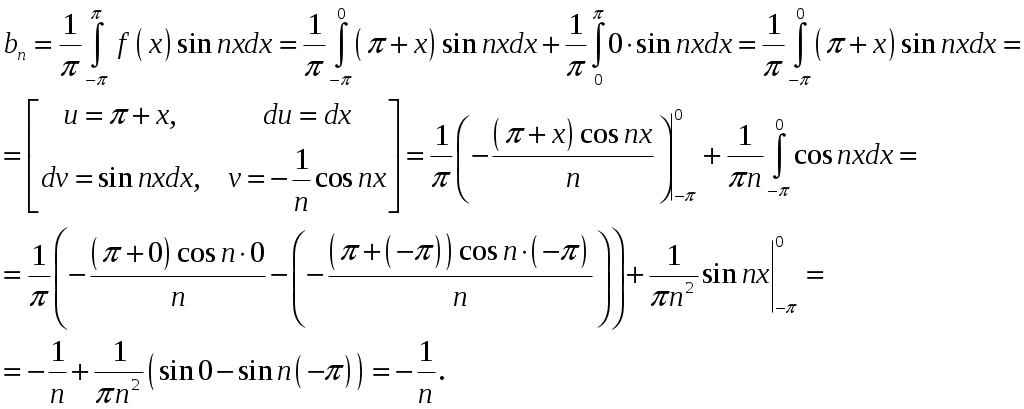 Разложение функции в ряд Фурье примет вид: 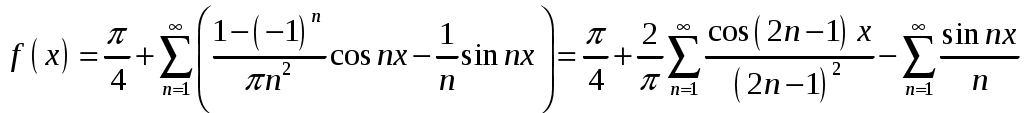 .Исследуем полученный ряд Фурье на сходимость. Согласно теореме Дирихле этот ряд сходится к заданной периодической функции с периодом  при всех  в точках разрыва  сумма ряда равна . . 3_2. Ряд Фурье функции 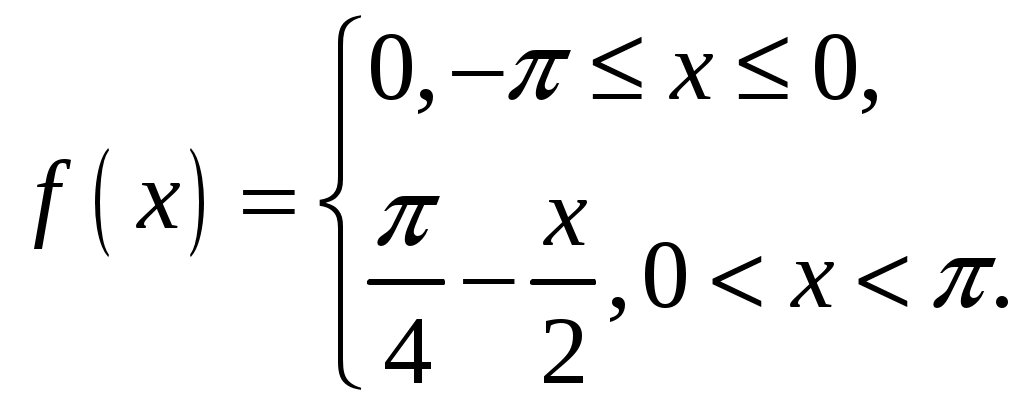 Решение. Разложение функции на интервале в ряд Фурье имеет вид: . 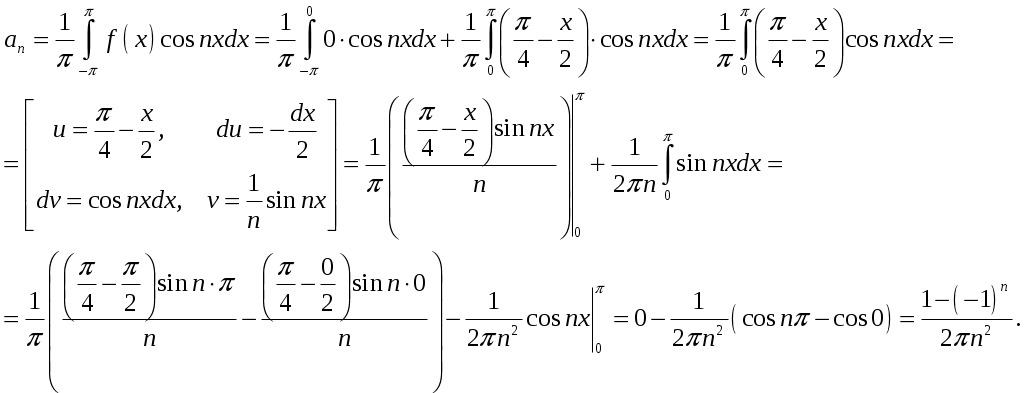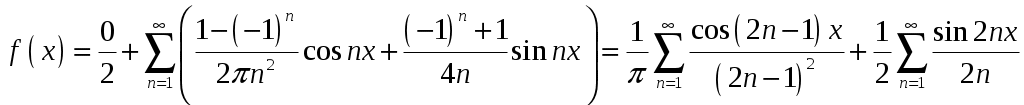, , .Находим коэффициенты ряда Фурье:    Разложение функции в ряд Фурье примет вид: .Исследуем полученный ряд Фурье на сходимость. Согласно теореме Дирихле этот ряд сходится к заданной периодической функции с периодом при всех в точках разрыва сумма ряда равна . . 3_4. Ряд Фурье функции  Решение. Разложение функции на интервале в ряд Фурье имеет вид: . , , .Находим коэффициенты ряда Фурье: 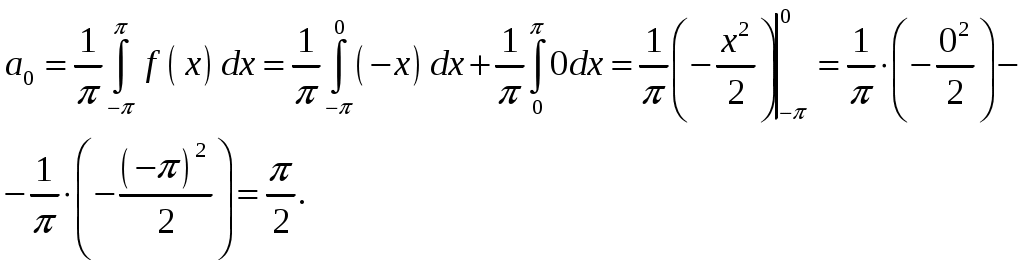 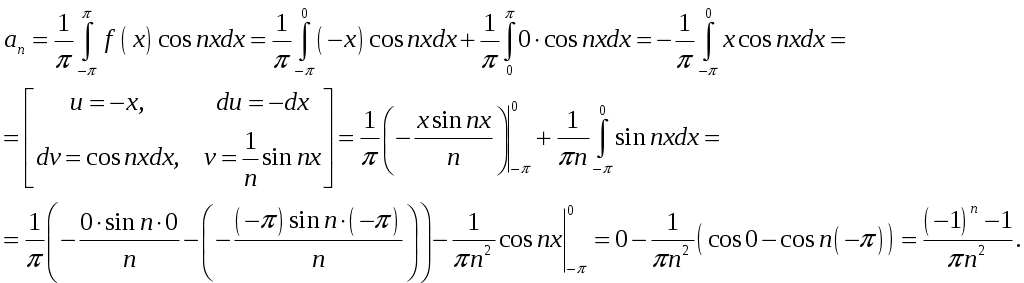 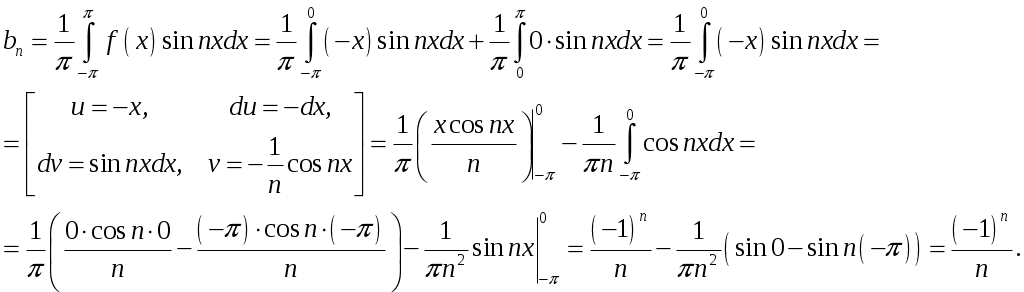 Разложение функции в ряд Фурье примет вид: 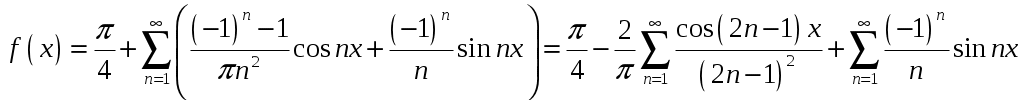 .Исследуем полученный ряд Фурье на сходимость. Согласно теореме Дирихле этот ряд сходится к заданной периодической функции с периодом при всех в точках разрыва сумма ряда равна . . 4_1. Найдите действительную и мнимую части функции  . Определите, является ли функция  аналитичной хотя бы в одной точке. Найдите производную в точках, в которых она существует.Решение. Так как 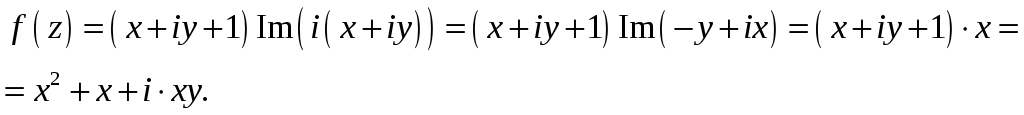 , то получим: Получаем:  , .Находим:     Проверим выполнение условий Коши-Римана:  ; . Очевидно, что условия Коши-Римана выполняются только в точке  , следовательно, функция является аналитической.Находим значение производной:  4_2. Найдите действительную и мнимую части функции  . Определите, является ли функция аналитичной хотя бы в одной точке. Найдите производную в точках, в которых она существует.Решение. Так как 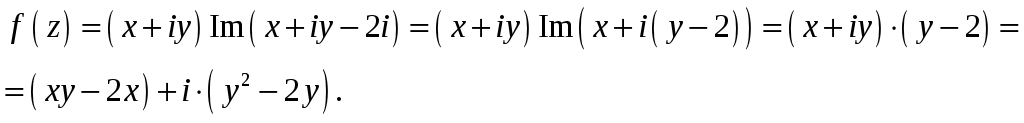, то получим: Получаем:  , .Находим:     Проверим выполнение условий Коши-Римана: ; . Очевидно, что условия Коши-Римана выполняются только в точке  , следовательно, функция является аналитической.Находим значение производной:  4_4. Найдите действительную и мнимую части функции  . Определите, является ли функция аналитичной хотя бы в одной точке. Найдите производную в точках, в которых она существует.Решение. Так как 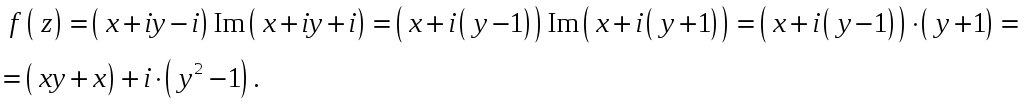, то получим: Получаем:  , .Находим:     Проверим выполнение условий Коши-Римана: ; . Очевидно, что условия Коши-Римана выполняются только в точке  , следовательно, функция является аналитической.Находим значение производной:  5_1. Восстановите аналитическую функцию в окрестности точки  по ее действительной части  и значению  .Решение. Так как заданная функция дифференцируема в любой точке, то функция  является действительной частью аналитической функции.Используя условия Коши–Римана, можно восстановить аналитическую функцию  по известной её мнимой или действительной части и заданном значении  .По условию задачи  ,  . Запишем условия Коши-Римана: , (1) . (2)Проинтегрировав соотношение (1) по переменной  , найдем мнимую часть функции . , где  – независящая от постоянная интегрирования. Найдём функцию . Продифференцируем найденную функцию  по переменной  и сравним с её значением (2). Имеем: .Значит,  , откуда  , где  .Таким образом,  ,  .Полагая , найд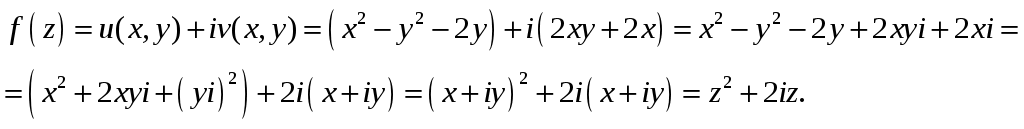ём  : ;  .Итак  Ответ:  5_2. Восстановите аналитическую функцию в окрестности точки по ее мнимой части  и значению  .Решение. Так как заданная функция дифференцируема в любой точке, то функция  является мнимой частью аналитической функции.Используя условия Коши–Римана, можно восстановить аналитическую функцию по известной её мнимой или действительной части и заданном значении .По условию задачи ,  . Запишем условия Коши-Римана:  , (1) (2)Проинтегрировав соотношение (1) по переменной , найдем мнимую часть функции . , где  – независящая от постоянная интегрирования. Найдём функцию . Продифференцируем найденную функцию  по переменной и сравним с её значением (2). Имеем:  .Значит, , откуда  , где .Таким образом,  ,  .Полагая , найдём : ;  .Итак,  Ответ:  .6_1. Вычислите интеграл  , если  :  .Решение. Контур интегрирования представляет собой окружность радиуса 2 с центром в точке  . Внутри контура находятся изолированные особые точки подынтегральной функции: точка  – полюс третьего порядка и  –простой полюс.Применяя первую теорему о вычетах, запишем: 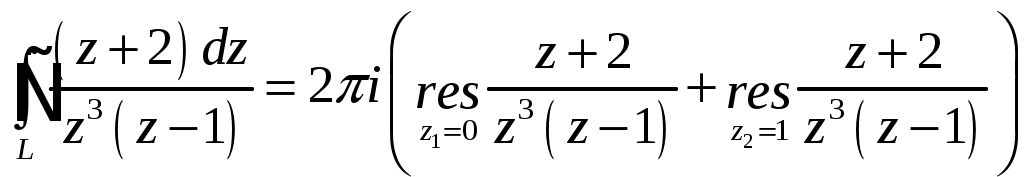 .  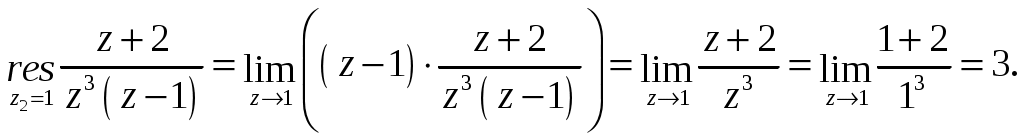Таким образом,  .Ответ: 0. 6_2. Вычислите интеграл  , если :  .Решение. Контур интегрирования представляет собой окружность радиуса 3 с центром в точке . Внутри контура находятся изолированные особые точки подынтегральной функции: точка  – простой полюс и  –простой полюс.Применяя первую теорему о вычетах, запишем: 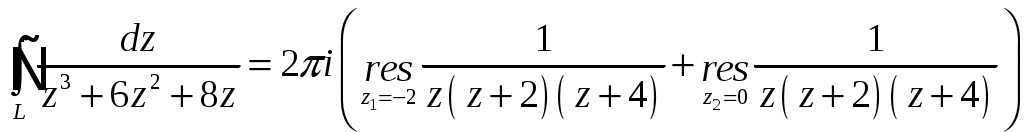 .  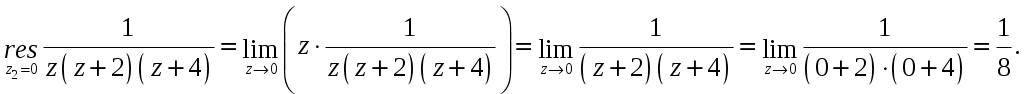Таким образом,  .Ответ:  .7_1. Разложение функции  в ряд Лорана в кольце  имеет вид.Решение. Разложим функцию на простейшие дроби:  . .Тогда:  .Получаем:  .7_3. Разложение функции  в ряд Лорана в кольце  имеет вид.Разложим функцию на простейшие дроби:  . .Тогда:  .Получаем:  . |