|
|
ПР1_БулановаАО. Контрольная работа по дисциплине Теория вероятности и математическая статистика Вариант 6
Министерство образование и науки Российской Федерации
Федеральное государственное бюджетное образовательное учреждение
высшего образование
“Владимирский государственный университет
имени Александра Григорьевича и Николая Григорьевича Столетовых”
(ВлГУ)
Контрольная работа
по дисциплине:
«Теория вероятности и математическая статистика»
Вариант №6
Выполнил:
студентка гр.ЗУКд-120
Буланова А. О.
Принял:
Мищенко З. В
Владимир 2022
1) В карточке спортлото 36 клеток. Играющий должен отметить 6. Каково число всех возможных вариантов?
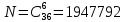
Сколькими способами можно выбрать четырех человек на 4 различные должности из 15 кандидатов на эти должности?
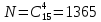
3) В группе 28 студентов. Сколькими способами можно избрать 6 делегатов на профсоюзную конференцию?
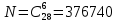
Правление фирмы выбирает трех человек на различные должности из 10 кандидатов. Сколькими способами это можно сделать?
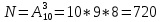
Сколькими способами можно выбрать 6 пирожных в кондитерской, где есть 4 разных сорта пирожных?
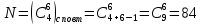
6) Из 20 милиционеров необходимо составить наряд из 6 человек. Сколькими способами это можно сделать?
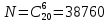
3) Куб, все грани которого окрашены распилен на 1000 кубиков одинакового размера, которые затем тщательно перемешаны. Найти вероятность того, что наудачу извлеченный кубик будет иметь окрашенных граней а) одну, б) две, в) три.
Испытание: извлечение кубика из тысячи.
Общее число возможных элементарных исходов 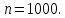
Решение в)
Обозначим через A событие (Кубик имеет три окрашенные грани).
Число благоприятствующих исходов m=8m=8. При указанном способе распила будет всего 8 кубиков с тремя окрашенными гранями.
Искомая вероятность 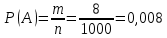
Решение б)
Обозначим через A событие {Кубик имеет две окрашенные грани}.
Число благоприятствующих исходов m=12⋅8=96. При указанном способе распила будет всего 96 кубиков с двумя окрашенными гранями.
Искомая вероятность 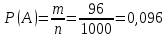
Решение а)
Обозначим через A событие {Кубик имеет одну окрашенную грань}.
Число благоприятствующих исходов m=8⋅8⋅6=384. При указанном способе распила будет всего 384 кубика с одной окрашенной гранью.
Искомая вероятность 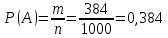
Ответ. а) 0,384; б) 0,096; в) 0,008.
4) При стрельбе относительная частота попаданий оказалась равной 0.85. Найти число попаданий, если всего было произведено 120 выстрелов.
Из формулы: 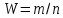
следует, что m = W · n.
Так как W = 0,85, n = 120, то m = 0,85 · 120 = 102. Таким образом, было получено 102 попадания.
Ответ: 102.
5) Участники жеребьевки тянут из ящика жетоны с номерами от 1 до 100. Найти вероятность того, что номер первого наудачу извлеченного жетона не содержит цифры 5.
Испытание: извлечение жетона из ящика.
Обозначим через A событие (Номер жетона не содержит цифры 5).
Общее число возможных элементарных исходов n=100.
Число не благоприятствующих исходов 19. При извлечении 5, 15, 25, 35, 45, 65, 75, 85, 95 или номеров между 50 и 59 включительно.
Число благоприятствующих исходов m=100 - 19 = 81.
Искомая вероятность 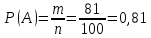
Ответ: p = 0,81.
6)Набирая номер телефона, абонент забыл последние 2 цифры и, помня лишь то, что эти цифры различны набрал их наудачу. Найти вероятность того, что набраны нужные цифры.
Благоприятствующий исход здесь один – правильный набор последних цифр m=1. Всех возможных исходов здесь будет столько, сколько можно составить комбинаций из 2 цифр, порядок которых имеет значение, значит
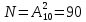 . Значит вероятность того, что номер набран правильно (событие . Значит вероятность того, что номер набран правильно (событие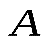 ): ): 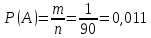
7) В ящике из 10 деталей 7 стандартных. Найти вероятность того, что среди взятых на удачу 6 деталей 4 стандартных. (Это, так называемая задача о выборке, обобщите ее и составьте аналогичные.)
Общее число возможных элементарных исходов испытания равно числу способов, которыми можно извлечь 6 деталей из 10, т.е. числу сочетаний из 10 элементов по 6 элементов 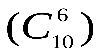 . .
Определяем число исходов, благоприятствующих событию 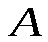 - «среди 6 взятых деталей 4 стандартных». Четыре стандартные детали из семи стандартных можно взять - «среди 6 взятых деталей 4 стандартных». Четыре стандартные детали из семи стандартных можно взять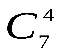 способами, при этом остальные 6-4=2 детали должны быть нестандартными; взять же две нестандартные детали из 10-7=3 нестандартных деталей можно способами, при этом остальные 6-4=2 детали должны быть нестандартными; взять же две нестандартные детали из 10-7=3 нестандартных деталей можно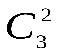 способами. Следовательно, число благоприятных исходов равно способами. Следовательно, число благоприятных исходов равно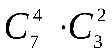 . .
Искомая вероятность равна отношению числа исходов, благоприятствующих событию, к числу всех элементарных исходов:
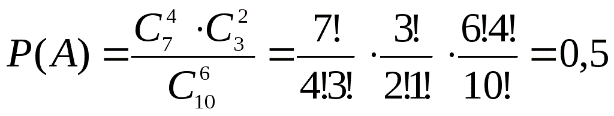 . .
8)Восемь различных книг расставляются рядом на одной полке. Найти вероятность того, что две определенные книги окажутся поставленными рядом.
Испытание: восемь различных книг расставлены на полке.
Обозначим через A событие (Две определенные книги оказались поставленными рядом).
Общее число возможных элементарных исходов nn равно числу всех возможных перестановок восьми различных книг:
n=P8=8!n=P8=8!.
Не теряя общности, можно предположить, что на полке имеется 8 пронумерованных мест, которые будут заняты данными книгами.
Событие A произойдет, если книги заняли места 1 и 2, или места 2 и 3, ..., или места 7 и 8. На это 7 возможностей.
Оказавшись рядом, 1-я книга может быть справа от 2-й или 1-я книга может быть слева от 2-й, то есть две возможности. По правилу произведения получаем 7⋅2=147⋅2=14 возможностей расположения двух книг рядом.
Остальные 6 мест могут быть заполнены различными перестановками оставшихся шести книг. Количество этих перестановок равно 6!.
Таким образом, еще раз применяя правило произведения получаем, что общее число возможных расстановок восьми различных книг, при которых две определенные книги окажутся поставленными рядом, равно
m=7⋅2!⋅6!m=7⋅2!⋅6!.
То есть, число благоприятствующих исходов m=7⋅2!⋅6!m=7⋅2!⋅6!.
Искомая вероятность равна
P(A)=mn=7⋅2!⋅6!8!=7⋅2⋅1⋅6!8⋅7⋅6!=14P(A)=mn=7⋅2!⋅6!8!=7⋅2⋅1⋅6!8⋅7⋅6!=14.
1) В магазин поступило 30 телевизоров, 5 среди которых имеют скрытые дефекты. Наудачу отбираются 2 телевизора для проверки. Какова вероятность того, что оба они не имеют дефектов?
Вероятность того, что первый телевизор окажется с дефектом 5 / 30 = 1 / 6.
Вероятность того, что второй отобранный телевизор окажется с дефектом 4 / 29.
Следовательно, вероятность того, что отобранные телевизоры не имеют скрытых дефектов (событие А), равна:
P * (A) = (1 / 6) * (4 / 29) = 4 / 174 = 2 / 87 0,023.
Ответ: Вероятность того, что оба отобранных телевизоров не имеют дефектов равна 0,023.
2) Вероятность безотказной работы двух независимо работающих сигнализаторов равна 0.6 и 0.7. Найти вероятность того, что сработают: а) оба сигнализатора, б) хотя бы один сигнализатор.
0,6 и 0,7 – работают и 0,4 и 0,3 - отказ
а) сработают ОБА - событие "И" - произведение вероятностей.
Ра = 0,4*0,3 = 0,12 = 12%
б) событие "ИЛИ" первый или второй
Рб = p1*q2 + q1*p2 = 0,6*0,3 + 0,4*0,7 = 0,18 + 0,28 = 0,46 = 46%
6) В партии деталей 12 стандартных изделий и 3 нестандартных. 5 деталей, выбранных наудачу, проверяют на соответствие стандарту. Найти вероятность того, что среди них не окажется нестандартных.
1-я деталь стандартная 12/15; 2-я деталь стандартная 11/14; 3-я деталь стандартная 10/13; 4-я деталь стандартная 9/12; 5-я деталь стандартная 8/11;
И всё перемножаем р=0,254
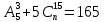
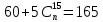
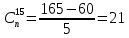
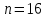 |
|
|
 Скачать 34.49 Kb.
Скачать 34.49 Kb.