явление переноса импульса. Контрольная работа по дисциплине Явление переноса в хт Вариант 8 Студента
 Скачать 0.58 Mb. Скачать 0.58 Mb.
|
|
Министерство науки и высшего образования России Федеральное государственное бюджетное образовательное учреждение высшего образования «ВОЛГОГРАДСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ» (ВолгГТУ) Контрольная работа по дисциплине «Явление переноса в ХТ»Вариант № 8
Волгоград – 2021 Определить режим течения жидкости в межтрубном пространстве теплообменника типа «труба в трубе» при следующих условиях: массовый расход жидкости Qm = 3290 кг/ч; диаметр внутренней трубы теплообменника d = 22×2 мм; диаметр внешней трубы теплообменника D = 54×2мм; плотность жидкости ρ = 1150 кг/м3; динамический коэффициент вязкости жидкости μ = 1,2·10-3 Па·с. 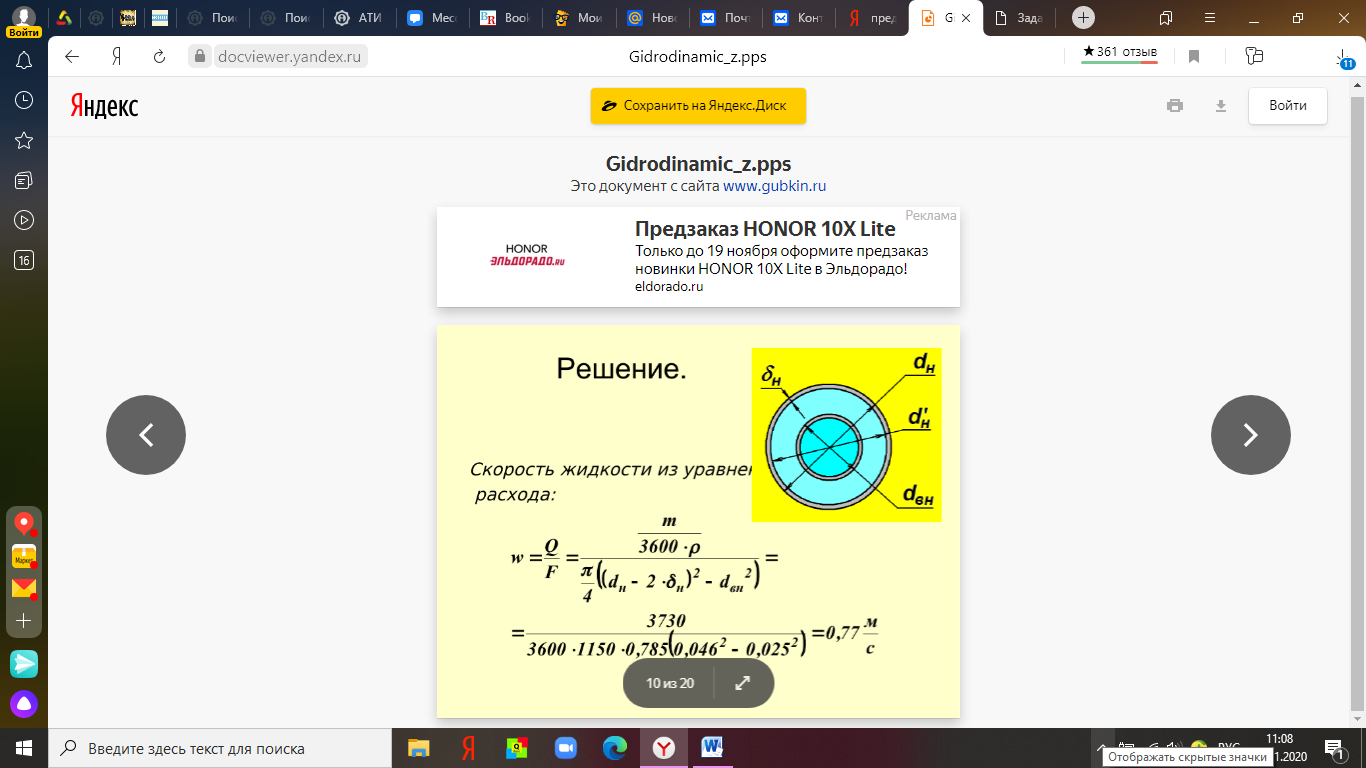 Решение: Решение:Скорость жидкости из уравнения расхода: W= 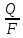 = = 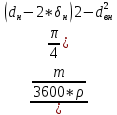 = =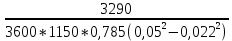 =0,5 м/с =0,5 м/сЕсли обозначить внутренний диаметр наружной трубы через dн’, то гидравлический (эквивалентный) диаметр кольцевого сечения: dгидр= 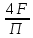 = =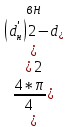 = dн’- dвн=0,05-0,022=0,028м = dн’- dвн=0,05-0,022=0,028мКритерий Рейнольдса: Re= 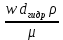 = =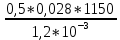 =13417 =13417Следовательно, режим течения турбулентный. 2. По трубам одноходового кожухотрубчатого теплообменникапроходит воздух при средней температуре 56°С и давлении (по манометру) 2 кгс/см2 со скоростью 11 м/с. Барометрическое давление 740 мм.рт.ст. Наружный диаметр труб 20 мм, толщина стенки 2,5 мм. Число труб 50. Определить: 1) Массовый расход воздуха; 2) Объемный расход воздуха при рабочих условиях; 3) Объемный расход воздуха при нормальных условиях; Решение: Плотность воздуха при нормальных условиях Ро=1,293 кг/м3 Рабочее давление (абсолютное): р=рбар+рман=740*133,3+98100*2=294800 Па мм рт.ст. или р=рбар+рман=740+735*2=2210 мм рт.ст. Плотность воздуха при рабочих условиях: ρ=ρ0 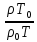 =1,293* =1,293* 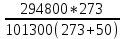 =3,18 кг/м3 =3,18 кг/м3или ρ=ρ0 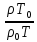 =1,293* =1,293*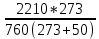 =3,18 кг/м3 =3,18 кг/м3Массовый расход воздуха: m= Q*ρ=wFρ=wn 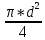 ρ=11*50*0,785*0,0162*3,18=0,35 кг/с ρ=11*50*0,785*0,0162*3,18=0,35 кг/сОбъемный расход воздуха при рабочих условиях: Q= 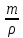 = =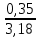 =0,11 м3/с =0,11 м3/сОбъемный расход воздуха при нормальных условиях: Q0= 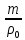 = = 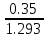 = 0.27 м3/с = 0.27 м3/с3. Движение хлористого водорода в трубопроводе диаметром 490 мм при 450 °С изучается на модели (масштаб 1:10), через которую продувается воздух при 25°С. Хлористый водород движется по трубопроводу при помощи газодувки со скоростью 11 м/сек, плотность газа ρ1 = 0,569 кг/м3 , вязкость μ1 = 0,0333·10-3 Па·с. Определить: 1) Условия гидродинамического подобия в трубопроводе и модели; 2) Скорость, с которой надо продувать воздух в модели для того, чтобы воспроизвести в ней движение газа в трубопроводе. Решение : Обозначим соответствующие величины для трубопровода индексом 1и для модели –индексом 2. Тогда условие гидродинамического пособия можно записать так: 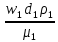 = =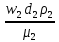 По заданию w=11 м/сек, d1=490 мм, d2= 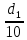 =49 мм. =49 мм.При 25°С плотность воздуха ρ2=1,18 кг/м3 , вязкость воздуха 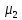 =0,018*10-3 н*сек/м3. =0,018*10-3 н*сек/м3.Из условия гидродинамического пособия следует, что необходимая скорость воздуха в модели должна составлять: W2= 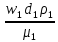 * *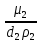 = = 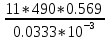 * *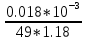 = 28.7 м/сек. = 28.7 м/сек.4. Мерник диаметром 1,5 м и высотой 2,3 м освобождается через отверстие в боковой стенке. Диаметр отверстия 15 мм, ось его находится на высоте 60 мм от днища мерника. Мерник сообщается с атмосферой, его начальная степень заполнения 0,95. Определить продолжительность полного истечения жидкости из мерника Решение: Натальная высота столба вытекающей жидкости в мернике над осью штуцера: Н1=0,85Н-h=0,85*2,3-0,06=1,89 м При истечении патрубок сжатие струи происходит внутри патрубка, его выходное сечение целиком наполнено жидкостью. Поэтому α = εφ= 1*0,82=0,82 Площадь сечения мерника: S= 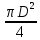 =0.785*1.52=1.77 м2 =0.785*1.52=1.77 м2Площадь сечения штуцера: S= 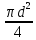 =0.785*0.0152= 5.89*10-4 м2 =0.785*0.0152= 5.89*10-4 м2Продолжительность полного опорожнения мерника рассчитываем по формуле: τ= 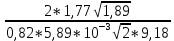 =2435 сек или 41 мин =2435 сек или 41 мин5. Вычислить значения скоростей движения в прямой трубе диаметром 50*2,5 мм, при которых потоки перестают быть ламинарными для: а) газа при рабс= 1 атм и температуре 20°С; б) длянефтяного масла плотности 990 кг/м3 имеющего динамическую вязкость 38,0*10-3 Па·с Решение: Критическое значение критерия Рейнольдса, при котором поток любой текучей среды внутри закрытого канала теряет ламинарный характер, равно 2300. Следовательно, искомые значения скоростей находятся из выражения критерия Рейнольдса ω= 2300 μ/(pd) а) для потока СО ω= 2300*0,0175*10-3/[1,25(0,050-2*0,0025)]=0,716 м/с б) для потока нефтяного масла ω=2300*38,0*10-3/[0,99*103(0,050-2*0,0025) ]=1,96 м/с 6. На трубопроводе имеется переход с диаметра 65 мм на диаметр 85 мм (диаметры внутренние). По трубопроводу движется вода, имеющая температуру 20ºС. Её скорость в узком сечении 1,8 м/с. Определить: 1. объёмный и массовый расходы воды; 2. скорость воды в широком сечении υ2; 3. режимы течения в узком и широком сечениях. Решение: Уравнение материального баланса (его ещё называют уравнением неразрывности потока) для наших выбранных сечений можно записать так G1 = G2 Помня, что G =V*ρ , можно записать уравнение так V1ρ1 =V2ρ2 распишем объёмный расход V S1w1 ρ1 = S2w2 ρ2 Так как наши потоки – трубы, т.е. имеют круглое сечение, то уравнение можно записать так 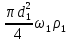 = =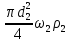 или после сокращения d12w1p1= d22w2p2 или после сокращения d12w1p1= d22w2p2Конкретно для нашей задачи мы можем допустить, что вода при переходе из Одного сечения в другое не изменяет свою плотность, ρ1=ρ2. Тогда получаем уравнение: 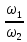 = =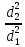 = = 2 2Т.е. получаем, что скорость потока в трубе обратно пропорциональна квадрату её диаметра. Следовательно, при увеличении диаметра в 2 раза скорость уменьшается в 4 раза! А если диаметр уменьшился в 3 раза, то скорость возрастёт в 9 раз. Определим объёмный и массовый расходы воды: V= S1ω1=  = = *1.8=0,059 м3/c *1.8=0,059 м3/cМассовый расход воды будет равен G =Vρ =0,0059*990=5,8 кг/с Скорость воды в широком сечении ω2= ω1  2=1,8*( 2=1,8*( 2=0,307 м/с 2=0,307 м/сКритерий Рейнольдса для узкого сечения Re1=  = = =115830 =115830Критерий Рейнольдса для широкого сечения Re2=  = = =25834 =258347. Труба диаметром 220*10 мм переходит в трубу диаметром 65*5 мм, послечего поднимается вверх на 12 м. В нижнем и верхнем сечениях трубы установлены манометры. Нижний манометр показывает давление 5,5 кГс/см2. По трубопроводу перекачивается вода с расходом 65 м3/час и температурой 32ºС. Определить показания верхнего манометра Р2 кГс/см2. Наличием сил вязкости пренебречь. Решение:  Начнём решение с эскиза. Вот наша труба, которая сначала «худеет», а потом резко поднимается на 12м. Нам надо определить, какое давление покажет манометр Р2. Запишем уравнение Бернулли для нижнего 1 и верхнего 2 сечений: z1+  + + = z2+ = z2+ + + Нам нужно найти Р2. Для этого необходимо сначала вычислить скорости воды в широкой и узкой трубах. Скорость воды в широкой трубе w1=  = =  =0,58 м/c =0,58 м/cСкорость воды в узкой трубе w2=  = =  =14,37 м/c =14,37 м/cТеперь выразим из уравнения Бернулли дробь   =z1-z2+ =z1-z2+ + + =-12+ =-12+ + + = 33 м = 33 мДля давления Р сделали переход из кГс/см2 в паскали (Па) путём умножения на переводной коэффициент 98100. Осталось перейти из напора в давление Р2=33*pg=33*992*9.8=320813 Па После перевода в кГс/см2 получим Р2=  =3,3 кГс/см2 =3,3 кГс/см28. По трубопроводу длиной 17 км и диаметром 125*5 мм перекачивается бензол с расходом 12 т/час при средней температуре 20ºС. Стенки трубопровода гладкие. Манометр, установленный в начале, показывает давление 6,5 ат. Определить показание манометра, установленного в конце трубопровода. Решение: Вычислим скорость бензола в трубе. w1=  = = = 0,33 м/с = 0,33 м/сНайдём значение критерия Рейнольдса Re=  = =  =49089 =49089 По формуле Блазиуса определим значение коэффициента трения λ=  = = = 0.02 = 0.02По уравнению Дарси-Вейсбаха определим потерю давления ΔP= λ*  * * = 0.02* = 0.02* * * = 147936 Па= = 147936 Па=  = 1,5 кГс/см2 = 1,5 кГс/см2Итак, потеря давления составила 1,5 кГс/см2, второй манометр покажет 5,0 кГс/см2. 9. Определить максимальную и среднюю скорости воздуха, его объемный расход при рабочих и нормальных условиях, массовый расход при следующих исходных данных: - давление в трубопроводе атмосферное; - диаметр трубопровода 51*2,5 мм; - температура воздуха 400С; - показания водяного дифманометра, подключенного к трубке Пито-Прандтля, составляет 13мм; Трубка Пито-Прандтля установлена вдоль оси воздухопровода. Решение:  Рис. 1 – Скоростная трубка Пито-Прандтля Длина прямо участка стабилизации скоростного профиля потока перед скоростной трубкой должна быть не менее 40 внутренних диаметров (калибров), т.е. 40(0,51-2*0,0025)=20,2 м. Считается, что условие выполнено. Скорость воздуха на оси трубопровода вычисляется по формуле: Wм=√2*9,81*  0,013=15,0 м/с 0,013=15,0 м/сЗначение критерия Рейнольдса по максимальной скорости Reм=15,0*0,152*1,13/0,019*10-3=135600 W=15,0*0,81=12,15 м/с Объемный расход при рабочих условиях Vс=12,15*0,785*0,1522=0,220 м3/с Пересчет на нормальные условия 0,220*273/(273+40)=0,192 м3/с Массовый расход воздуха Мс= 0,220*1,12=0,192*1,293=0,247 кг/с. 10. Вычислить потерю давления на преодоление сил трения при прохождении воды по змеевику со скоростью 1,4 м/с при температуре 300С. Диаметр стальной трубы с незначительной коррозией 43*2,5 мм. Число витков 13, диаметр витков 1,0 м. Решение: Определяем значение критерия Рейнольдса: Re=1,4*0,038*1000/0,8*10-3=66500 Средняя шероховатость цельнотянутой стальной трубы с незначительной коррозией е=0,2 мм, тогда dэ/е=38/0,2=190. Коэффициент трения при Re=66500 и dэ/е=190 определяем что λ= 0,0320 Длина трубы змеевика L= πDn=3.14*13*1,0=40,8 м Потеря давления при прохождении потока воды по змеевику: Δρтр.зм.=(1+3,54*0,038/1,0)0,0320(40,8/0,038)1000*1,22/2=28065 Па = 28065/9,81=2861 мм вод. ст. |
