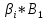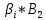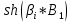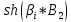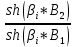Сыродубов работа. Контрольная работа по дисциплинемеждисциплинарному курсу Электротехнические материалы
 Скачать 164.09 Kb. Скачать 164.09 Kb.
|
|
МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ федеральное государственное автономное образовательное учреждение высшего образования «Северный (Арктический) федеральный университет имени М.В. Ломоносова» ВШЭНиГ КОНТРОЛЬНАЯ РАБОТА
Архангельск 2020 СОДЕРЖАНИЕ
Задача 1. Опорный стержневой керамический изолятор ОНС изолирует и поддерживает шины контактных деталей в открытом распределительном устройстве. Изолятор представляет собой сплошной круглый стержень с выступающими ребрами. На торцевых частях изолятора закреплены металлические фланцы (колпаки), являющиеся электродами (рис.1). 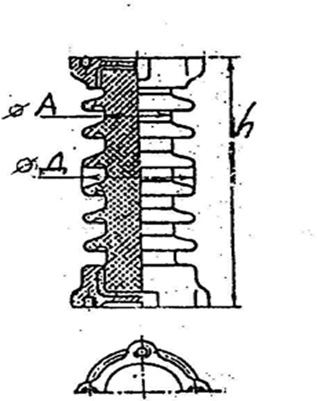 Рисунок 1. Конструкция опорного изолятора ОНС наружной установки Определить полный ток утечки, протекающий в изоляторе, емкость идиэлектрические потери в нем, если известны: - материал изолятора 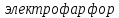 ; ;- номинальное напряжение на нем 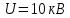 ; ;- частота электрического поля 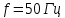 ; ;- удельное объемное сопротивление 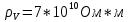 ; ;- удельное поверхностное сопротивление 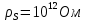 ; ;- относительная диэлектрическая проницаемость 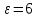 ; ;- тангенс угла диэлектрических потерь 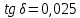 ; ;- высота изолятора 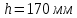 ; ;- диаметр 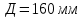 ; ;- диаметр 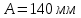 . .Решение: Рассчитаем сначала сопротивление току при протекании через объем диэлектрика: 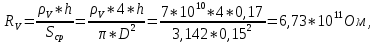 где средний диаметр 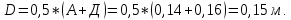 Рассчитаем поверхностное сопротивление: 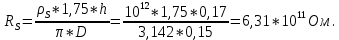 Определяем эквивалентное сопротивление такого изолятора: 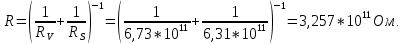 Тогда ток утечки можно найти по закону Ома: 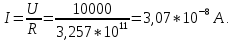 Определим емкость такого изолятора: 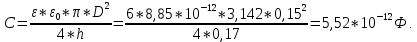 Тогда искомые диэлектрические потери в изоляторе можно вычислить следующим образом: 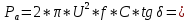 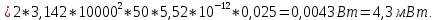 Задача 2. Питание электрической установки осуществляется трехфазным током с помощью трех свинцовых высоковольтных кабелей. Определить ёмкость одного свинцового высоковольтного кабеля, минимальную и максимальную напряженности электрического поля в изоляции кабеля и реактивную (зарядовую) мощность в нём, если известны: - линейное напряжение 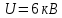 ; ;- частота поля 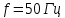 ; ;- сечение алюминиевой жилы кабеля 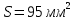 ; ;- толщина бумажной пропитанной изоляции 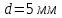 с диэлектрической проницаемостью с диэлектрической проницаемостью 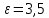 ; ;- длина кабеля 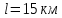 . .Решение: По теореме Гаусса, напряженность электрического поля по толщине изоляции выражается формулой: 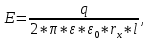 где q - заряд жилы кабеля, Кл; 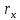 - переменная величина, м; l- длина кабеля, м; Е - напряженность электрического поля, кВ/м. - переменная величина, м; l- длина кабеля, м; Е - напряженность электрического поля, кВ/м.Напряжение между жилой кабеля и свинцовой оболочкой выражается через интеграл вектора напряженности: 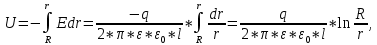 где R=r+d- внутренний радиус свинцовой оболочки, мм; r - радиус медной жилы, мм; d - толщина изоляции, мм; U - напряжение, кВ. Радиус жилы кабеля: 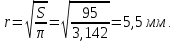 Емкость кабеля определяется как отношения заряда к напряжению: 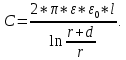 Тогда максимальная напряженность в изоляции кабеля: 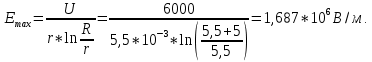 Минимальная напряженность в изоляции кабеля: 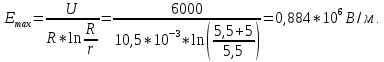 Рассчитываем емкость кабеля: 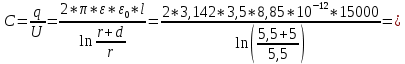 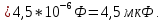 Реактивная мощность в кабеле (зарядная) определяется из выражения: 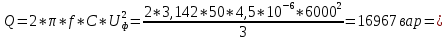 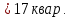 Задача 3. Электрическая установка, имеющая мощность 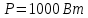 питается от электрической сети напряжением питается от электрической сети напряжением 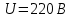 . Питающая линия выполненамедными проводами сечением . Питающая линия выполненамедными проводами сечением 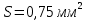 с полиэтиленовой изоляцией, имеющими предельно допустимую температуру нагрева с полиэтиленовой изоляцией, имеющими предельно допустимую температуру нагрева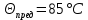 и коэффициент теплопередачи и коэффициент теплопередачи 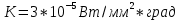 . .Рассчитать допустимую по условиям нагрева плотность тока и допустимый ток, сравнить его с рабочим током и определить надежность и экономичность работы установки c данными проводами. Решение: Количество теплоты, выделяемое в проводе, определяется выражением: 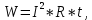 где W - количество теплоты, Вт; t - время, с. Часть этого тепла идет на повышение температуры провода, а другая часть рассеивается в окружающей среде. Уравнение теплового баланса имеет следующий вид: 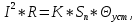 где 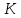 - коэффициент теплоотдачи, - коэффициент теплоотдачи, 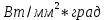 ; ; 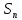 - поверхность охлаждения провода, мм2; - поверхность охлаждения провода, мм2; 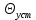 - установившаяся разность температур провода и окружающей среды: - установившаяся разность температур провода и окружающей среды: 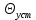 =85-20=65 °C. =85-20=65 °C.Удельное сопротивление меди при 20°С, равно ρ20=1,78·10-8Ом·м, температурный коэффициент сопротивления α=0,0038 К-1. Следовательно, удельное сопротивление меди при 85°C будет равно: 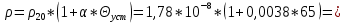 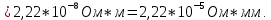 Диаметр провода: 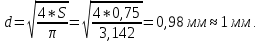 Таким образом: 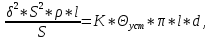 откуда получаем выражение для допустимой плотности тока: 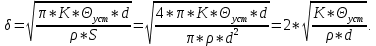 Найдём допустимую плотность тока: 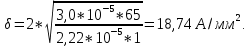 Определяем допустимый ток: 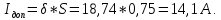 Рабочий ток определяется по формуле Джоуля-Ленца: 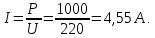 Следовательно, данная проводка сможет выдержать при длительной эксплуатации на токе 4,55А, более чем с 3-кратным запасом. Задача 4. Выполнить аппроксимацию кривой намагничивания №6 трансформатора (рисунок 2) в виде зависимости 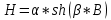 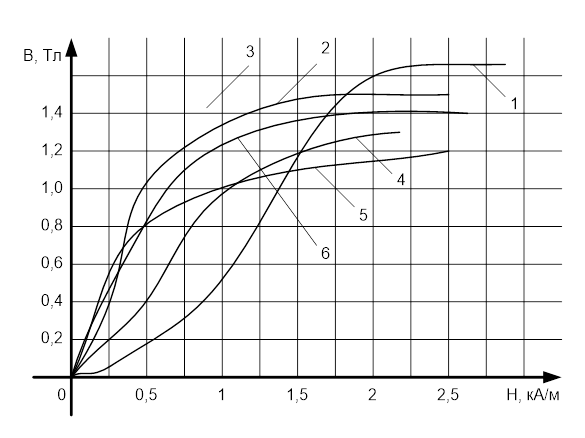 Рисунок 2 Решение: На заданной кривой №6 (рисунок 2) выбираем две произвольные точки: 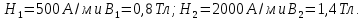 Составляем систему уравнений: 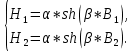 В имеющихся числовых значениях это составит: 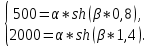 Делим второе уравнение системы на первое: 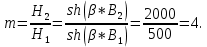 Задаемся пятью значениями 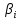 и вычисляем гиперболические синусы соответствующих аргументов. Результат расчета сводим в таблицу 1. и вычисляем гиперболические синусы соответствующих аргументов. Результат расчета сводим в таблицу 1.Таблица 1
На основании данных таблицы 1 строим на рисунке 3 соответствующую графическую зависимость: 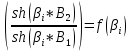 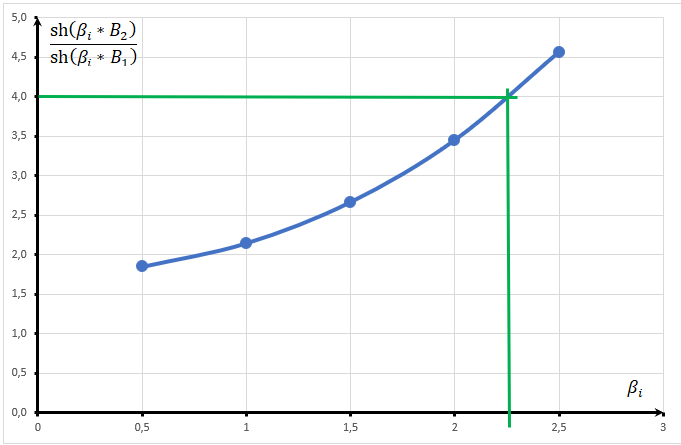 Рисунок 3 По рисунку 3 при имеющемся 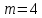 определяем соответствующее значение определяем соответствующее значение 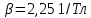 . . Рассчитываем коэффициент: 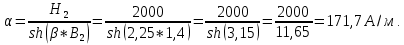 Таким образом, искомая зависимость получена в виде: 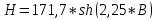 СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ 1. Пасынков В.В., Сорокин B.C. Материалы электронной техники: Учебник для вузов — СПб.: Издательство "Лань", 2009. 2. Богородицкий Н.П., Пасынков В.В., Тареев Б.М. Электрические материалы: Учебник для вузов — Д.: Энергоатомиздат, 1985. 3. Серебряков А.С. Электротехническое материаловедение. Электроизоляционные материалы: Учебное пособие для вузов ж.-д. транспорта. - М.: Маршрут, 2005.- 280 с. 4. Серебряков А.С. Электротехническое материаловедение. Проводниковые, полупроводниковые и магнитные материалы: Учебное пособие для вузов ж.-д. транспорта. - М.: «Издательский дом «Транспортная книга», 2008. - 372 с. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||