Контрольная работа за 1 полугодие. 1 полугодие к.р.. Контрольная работа по геометрии за iе полугодие. 9 класс

• Название: Контрольная работа по геометрии за iе полугодие. 9 класс
• Анкор: Контрольная работа за 1 полугодие
• Дата: 07.04.2022
• Размер: 60.5 Kb.
• Имя файла: 1 полугодие к.р..doc
• Тип: Контрольная работа; #449839

Контрольная работа по геометрии за I-е полугодие. 9 класс

Вариант 1.
Часть 1

1. В трапеции ABCD, основания которой равны 5 и 8 см, MN – средняя линия.

Отрезок BE параллелен стороне CD. Найдите длину отрезка MK.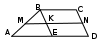




Ответ:__________________
2. 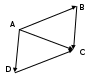Какие из равенств являются верными? Укажите в ответе их номера.

1. 2. 3.

Ответ:__________________
3. Начертите два неколлинеарных вектора a и b. Постройте векторы, равные:

а) 2a +3b; б) a – b.

4. 
   Даны векторы: a {6; -4}, b =i-2j, c= a + 2b. Найдите координаты вектора с.
   
5. 
   Даны векторы: a {6; -4}, b =i-2j, c= a + 2b. Найдите длину вектора с.
   
6. 
   Выберите верные утверждения, запишите их номера без пробелов и запятых:
   

1) Вектор — это направленный отрезок, для которого указано, какая из его точек является началом, а какая концом.

2) Векторы называются противоположными, если они сонаправлены и длины их равны.

3) Средняя линия трапеции — это отрезок, соединяющий середины её оснований

4) Каждая координата суммы двух и более векторов равна сумме соответствующих координат этих векторов

5) Вычисление длины вектора по его координатам вычисляется по формуле |a|=

4. 
   Найдите координаты центра окружности (х - 2)² + (у + 1)² = 16
   

1) (-2; 1) 2) (2; -1) 3) (1; -2) 4) (-1; 2)

Контрольная работа по геометрии за I-е полугодие. 9 класс

Вариант 2
Часть 1

1. В трапеции ABCF, основания которой равны 7 и 10 см, MN – средняя линия.

Отрезок BE параллелен стороне CF. Найдите длину отрезка MK.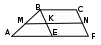




Ответ:__________________

2. Какие из равенств являются верными? Укажите в ответе их номера.

1. 
   2. 3.
   

Ответ:__________________
3. Начертите два неколлинеарных вектора c и d. Постройте векторы, равные:

а) 3c +2d; б) c – d.

4. 
   Даны векторы: b{-12;18}, a=2i+j, c=2a – b.Найдите координаты вектора с.
   

4. 
   Даны векторы: b{-12;18}, a=2i+j, c=2a – b. Найдите длину вектора с.
   
5. 
   Выберите верные утверждения, запишите их номера без пробелов и запятых:
   

1) От любой точки можно отложить вектор, равный данному и притом только один.

2) Векторы называются равными, если они сонаправлены

3) Средняя линия трапеции параллельна его основаниям и равна их полусумме

4) каждая координата суммы двух и более векторов равна разности соответствующих координат этих векторов.

5) Каждая координата середины отрезка равна полусумме соответствующих координат его концов.

4. 
   Найдите координаты центра окружности (х + 4)² + (у - 3)² = 9
   

1) (3; 4) 2) (-3; 4) 3) (-4; 3) 4) (4; -3)