Контрольная работа по гидравлике Вариант 2 Иванов И. И. г. Барнаул 2017 г. Задача 1

• Название: Контрольная работа по гидравлике Вариант 2 Иванов И. И. г. Барнаул 2017 г. Задача 1
• Дата: 13.10.2022
• Размер: 172.98 Kb.
• Имя файла: kr_hidravlika_2.docx
• Тип: Контрольная работа; #732663

Алтайский государственный технический университет

им. И. И. Ползунова

Контрольная работа

по гидравлике

Вариант 2

Выполнил: Иванов И. И.

г. Барнаул

2017 г.

Задача 1

Автоклав объемом 25,0 литров наполнен жидкостью и закрыт герметически. Коэффициент температурного расширения жидкости α = 832×10⁶ 1/˚С, ее модуль упругости Е = 1,95×10⁹ Па.

Определить повышение давления ∆p в автоклаве при увеличении температуры жидкости на величину ∆Т = 11,0 ˚С.

Объемной деформацией автоклава пренебречь.
Решение.

При изменении температуры жидкости ее объем изменяется, при этом изменение объема характеризуется коэффициентом температурного расширения α. Конечный объем V, который заняла бы жидкость, имеющая первоначальный объем V₀ в свободном состоянии, при изменении температуры на величину ∆Т может быть определен по формуле:

V = V₀(1 + α×∆Т) = 0,025(1 + 832×10^-6×11,0) ≈0,0252288 (м³), (1)

где V₀ = 25 л = 0,025 м³ – первоначальный объем жидкости.

Из формулы (1) следует, что если бы жидкость не была помещена в герметически закрытый автоклав, то ее объем увеличился бы на величину, пропорциональную коэффициенту объемного расширения.

Изменение объема при нагревании жидкости составит:

∆V = V – V₀ ≈ 0,0252288 - 0,025 ≈ 0,0002288 м³ ≈ (0,2288 л).
Поскольку по условию задачи жидкость помещена в герметичный жесткий автоклав, то увеличение ее объема невозможно, поэтому при повышении температуры жидкости в герметичном сосуде будет нарастать давление, величину которого можно определить, используя формулу для определения коэффициента сжимаемости βv (коэффициента объемного сжатия). Использование этого коэффициента при расчетах позволяет учитывать сжимаемость жидкости, и, соответственно, повышение давления в ее объеме.

Коэффициентом сжимаемости (коэффициентом объемного сжатия) называется отношение относительного изменения объема жидкости ΔV/V к изменению давления Δp в автоклаве:

βv = (ΔV/V)/Δp = (V- V₀)/V×Δp,

где V – объем жидкости после изменения ее температуры;

V₀ – начальный объем жидкости (объем автоклава).

Величину, обратную объемной сжимаемости, называют модулем объемного сжатия или модулем упругости Е (Па):

Е = 1/βv

Следует учитывать, что объемная сжимаемость не является постоянной характеристикой, она зависит от температуры жидкости и оказываемого на нее давления. Однако при давлениях, наиболее часто применяемых на практике в механизмах и устройствах, объемная сжимаемость жидкостей очень мала, и в обычных гидравлических расчетах ей пренебрегают, учитывая лишь в особых случаях, например, при расчетах некоторых гидроприводов и явлениях гидравлического удара.
Исходя из приведенных выше формул, учитывающих расчетный температурный прирост объема жидкости и связанное с этим повышение давления в автоклаве, можно записать:

βv = 1/Е = (ΔV/V)/Δp = [V₀ - V₀(1 + α×∆Т) / V₀(1 + α×∆Т)]/∆p =

= [1 - 1/(1 + α×∆Т)]/∆p,

откуда получаем:

∆p = Е[1 - 1/(1 + α×∆Т].

Анализ полученной формулы позволяет сделать вывод, что изменение давления жидкости, нагреваемой в герметичном сосуде, не зависит от объема этого сосуда (в нашем случае – автоклава).

Подставив в полученную формулу исходные данные задачи, получим прирост давления жидкости в автоклаве:
∆p = Е[1 - 1/(1 + α×∆Т] = 1,95×10⁹ (1 – 1/(1 + 832×10^-6×11,0) =

= 17 684 550 Па ≈ 17,68 МПа.
Ответ:

Повышение давления в автоклаве при нагреве находящейся в нем жидкости на 11,0 ˚С составит 17,68 МПа.
Задача 2

Определить скорость v равномерного скольжения прямоугольной пластины (a × b × c) по наклонной плоскости под углом α = 12˚ (sin 12˚ = 0,208), если между пластиной и плоскостью находится слой масла (по условию задачи – Турбинное масло) толщиной δ = 0,7 мм.

Температура масла Т = 30 ˚С.

Плотность материала пластины ρ = 240 кг/м³.

Размеры пластины: a = 400 мм; b = 250 мм; c = 43 мм.

Справочная информация:

Поскольку турбинные масла разных марок имеют различные физико-химические свойства, принимаем для решения задачи свойства масла турбинного Тп-22С (ТУ 38.101821-2001).

Физические свойства масла турбинного Тп-22С (ТУ 38.101821-2001):

- плотность ρ_м при Т = 15 ˚С – не более 903 кг/м^3.

По таблице изменения плотности нефтепродуктов в зависимости от температуры принимаем для расчетов плотность турбинного масла Тп-22Б равной 860 кг/м³;

- вязкость кинематическая v при 40°С - 28,8-35,2 мм²/с;

- вязкость кинематическая v при 50°С - 20,0-23,0 мм²/с;

В 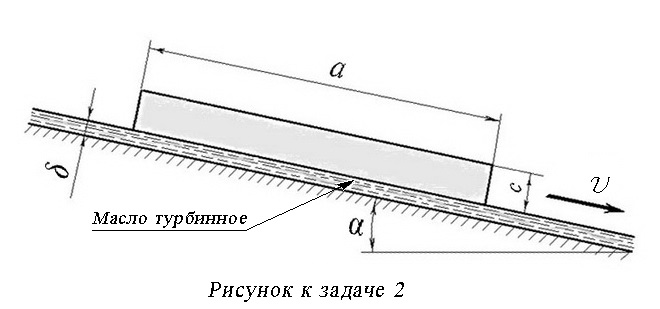соответствии с номограммой определения кинематической вязкости нефтепродуктов принимаем для расчета кинематическую вязкость турбинного масла Тп-22С при Т = 30˚С равной v = 42 мм²/с или v = 42×10^-6 м²/с.
Решение:
По условию задачи скольжение пластины по наклонной плоскости является прямолинейным и равномерным, следовательно, пластина находится в состоянии равновесия (тело находится в равновесии, если оно неподвижно либо перемещается равномерно и прямолинейно). Равновесное состояние любого тела характеризуется алгебраическим (векторным) равенством всех действующих на него внешних сил, поэтому можно сделать вывод, что силы, приводящие в движение пластину равны направленным в противоположную сторону силам сопротивления движению.

С учетом вышеизложенного, задача может быть решена с использованием закона Ньютона для внутреннего трения жидкости и условия равновесного состояния материальных тел (законов статики).

Если не принимать во внимание силу сопротивления воздуха, то скольжение пластины по наклонной плоскости осуществляется под воздействием горизонтальной составляющей силы тяжести G_г = G×sinα (движущая сила) и силы трения F_тр со стороны слоя турбинного масла между пластиной и наклонной плоскостью (сила сопротивления движению). Следовательно, можно записать:

G×sinα = F_тр (1)

Силу тяжести, действующую на пластину (вес пластины), можно определить, вычислив ее массу m с учетом габаритных размеров и плотности:

m = а×б×с×ρ = 0,40×0,25×0,043×240 = 1,032 кг;

где а, б и с – габаритные размеры пластины (в исходных данных к задаче);

ρ – плотность материала пластины (в исходных данных к задаче).

Тогда вес пластины будет равен:

G = m×g = 1,032×9,81 ≈ 10,124 (Н),

где g = 9,81 м/с² – ускорение свободного падения.

Теперь, используя формулу (1), можно определить силу трения слоя жидкости (в нашем случае – масла турбинного Тп-22С):

F_тр = G×sinα = 10,124×0,208 = 2,106 (Н).

В соответствии с законом Ньютона для внутреннего трения жидкости:

F_тр = μ×v×S/δ(2),

где v – скорость движения слоя жидкости на расстоянии δ от неподвижной плоскости (т. е. искомая скорость), м/с;

S = а×б = 0,40×0,25 - площадь поверхности пластины, м²;

μ – динамическая вязкость жидкости; μ = v×ρ_м, кг/м×с;

здесь vи ρ_м соответственно кинематическая вязкость и плотность жидкости (масла турбинного Тп-22С) – справочная информация.

Подставив формулы для определения динамической вязкости и площади пластины в формулу (2), запишем уравнение для определения внутреннего трения жидкости в виде:

F_тр = v×ρ×v×a×b/δ(3).

Из формулы (3) определяем искомую скорость v , с которой пластина прямолинейно и равномерно скользит вдоль наклонной плоскости по слою турбинного масла Тп-22С:

v = (F_тр×δ)/(v×ρ_м×a×b) =

= (2,106×0,7×10^-3)/(42×10^-6×860×0,40×0,25) ≈ 0,408 м/с.

Ответ:

Пластина скользит по наклонной плоскости с постоянной скоростью

v ≈ 0,408 м/с.

Задача 3

Центробежный насос, перекачивающий жидкость (керосин Т-1) при температуре 20 ˚С, развивает подачу Q = 1,4 л/с.

Определить допустимую высоту всасывания h_в, если длина всасывающего трубопровода l = 12,8 м, диаметр d = 40 мм, эквивалентная шероховатость ∆э = 0,070 мм, коэффициент сопротивления обратного клапана ζ_к = 6,4, а показание вакуумметра не превышало бы р₁ = 72,0 кПа.

Справочные величины:

- плотность керосина Т-1 при 20°С - 780 кг/м³;

- кинематическая вязкость керосина Т-1 при 20°С - 1,3×10^-6 м²/с (1,3 сСт).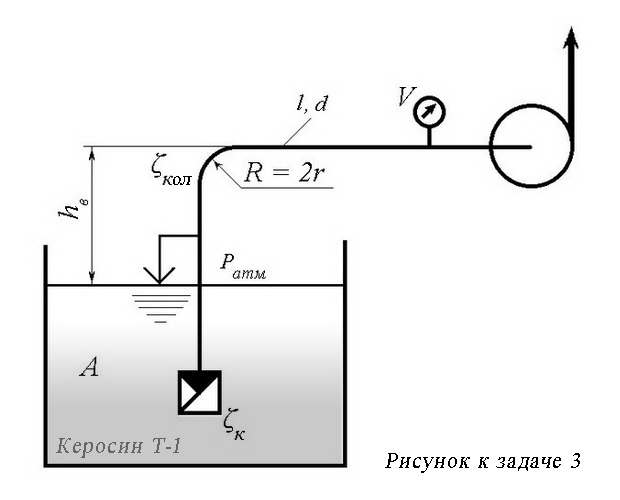



Решение:

Из уравнения Бернулли для двух сечений (в нашем случае - для уровня жидкости в приемном резервуаре и сечения на входе в насос) следует:

h_в = (p₀ - р_а)/ρg –v²/2g - h_f (1),

где h_в - искомая высота всасывания (м);

h_f- суммарные потери напора во всасывающем трубопроводе (м);

р_a  - атмосферное давление, Па;

р₀  - абсолютное давление на входе в насос, Па;

g– ускорение свободного падения; g = 9,81 м/с^-2;

v  - скорость движения жидкости (керосина Т-1) по трубе, м/с.

Разность давлений p₀ - р_а представляет собой показание вакуумметра на входе в насос p₁, поэтому уравнение Бернулли для заданной гидравлической системы можно записать в виде:

h_в = p₁/ρg –v²/2g - h_f (2),

Потери напора h_fво всасывающем трубопроводе складываются из потерь на трение h_l при движении жидкости по трубе и потерь на местные сопротивления h_м:

h_f = h_l + h_м = il + ∑ζv²/2g (3),

где i - потери напора на 1 м длины трубы;

l - длина трубопровода, м;

∑ζ - сумма коэффициентов местных сопротивлений;

v - скорость движения жидкости (керосина Т-1) по трубопроводу, м/с.

Для определения скорости керосина в трубе условно считаем, что его поток неразрывен.

Тогда можно использовать формулу для определения скорости движения жидкости по трубопроводу, зная сечение трубы S (м²) и объемную подачу насоса Q (м³/с):

v = Q/S = 4Q/πd² = (4×1,4×10^-3)/(3,14×0,04²) = 1,114 м/с.

Режим движения жидкости (в нашем случае – керосина Т-1) в трубопроводе можно прогнозировать с помощью числа Рейнольдса по формуле:

Re = vd/v,

где v = 1,05×10^-6 м²/с – кинематическая вязкость керосина Т-1, (справочная величина);

тогда число Рейнольдса будет равно:

Re = 1,114×0,04/1,3×10^-6 = 34276.

Полученное число Рейнольдсазначительно больше критического (Re_кр = 2000), поэтому режим движения жидкости (керосина Т-1) в трубопроводе является турбулентным.
Поскольку скорость движения жидкости (керосина Т-1) по трубе достаточно большая, а плотность керосина Т-1 при температуре 20 ˚С - ρ_к = 780 кг/м³,потери гидравлического напора на трение по длине трубы можно определить по «водопроводной» формуле, получаемой из формулы Шези:

h_l = il = lQ²/∆э ² = 12,8×(1,4×10^-3)²/0,07² ≈ 0,00512 м.

Местные сопротивления складываются из сопротивления обратного клапана ζ_ки сопротивления колена ζ_колимеющего закругление с радиусомR = 2d (см. рисунок к задаче 3).

ζ_кол = 0,5 – справочная информация.

Тогда местные сопротивления в трубопроводе будут равны:

h_м = ∑ζ v²/2g = (6,4+0,5)× 1,114²/(2×9,81) = 0,4364 (м).

Суммарные потери напора: h_f= h_l+ h_м = 0,00512 + 0,4364 = 0,4415 (м).

Подставив полученные расчетные данные в формулу (2), получим допустимую высоту всасывания h_в:

h_в = p₁/ρ_кg –v²/2g - h_f = (72,0×10³/780×9,81) – (1,114²/(2×9,81) – 0,4415 ≈

≈ 8,905 м.

Ответ:

Допустимая высота всасывания насоса - h_в ≈ 8,905 м.