гидравлика. Задачи04. Контрольная работа по курсу Гидравлика, гидравлические машины и гидропривод
 Скачать 245.93 Kb. Скачать 245.93 Kb.
|
|
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РФ Федеральное агентство по образованию Костромской государственный университет Кафедра ТПЛВ Контрольная работа по курсу «Гидравлика, гидравлические машины и гидропривод» Задачи Вариант №04 Выполнил: Бабарыкин М.А. 06-ЗА-004 Проверил: Куликов А.В., к.т.н., доцент Кострома 2007 Контрольная работа №1 Задача 3г. Горизонтальный цилиндрический резервуар, закрытый полусферическими днищами, заполнен жидкостью Ж. Длина цилиндрической части резервуара L, диаметр D. Манометр показывает манометрическое давление рМ. Температура жидкости 200 С. Определить силы, разрывающие резервуар по сечениям 1-1, 2-2, 3-3. 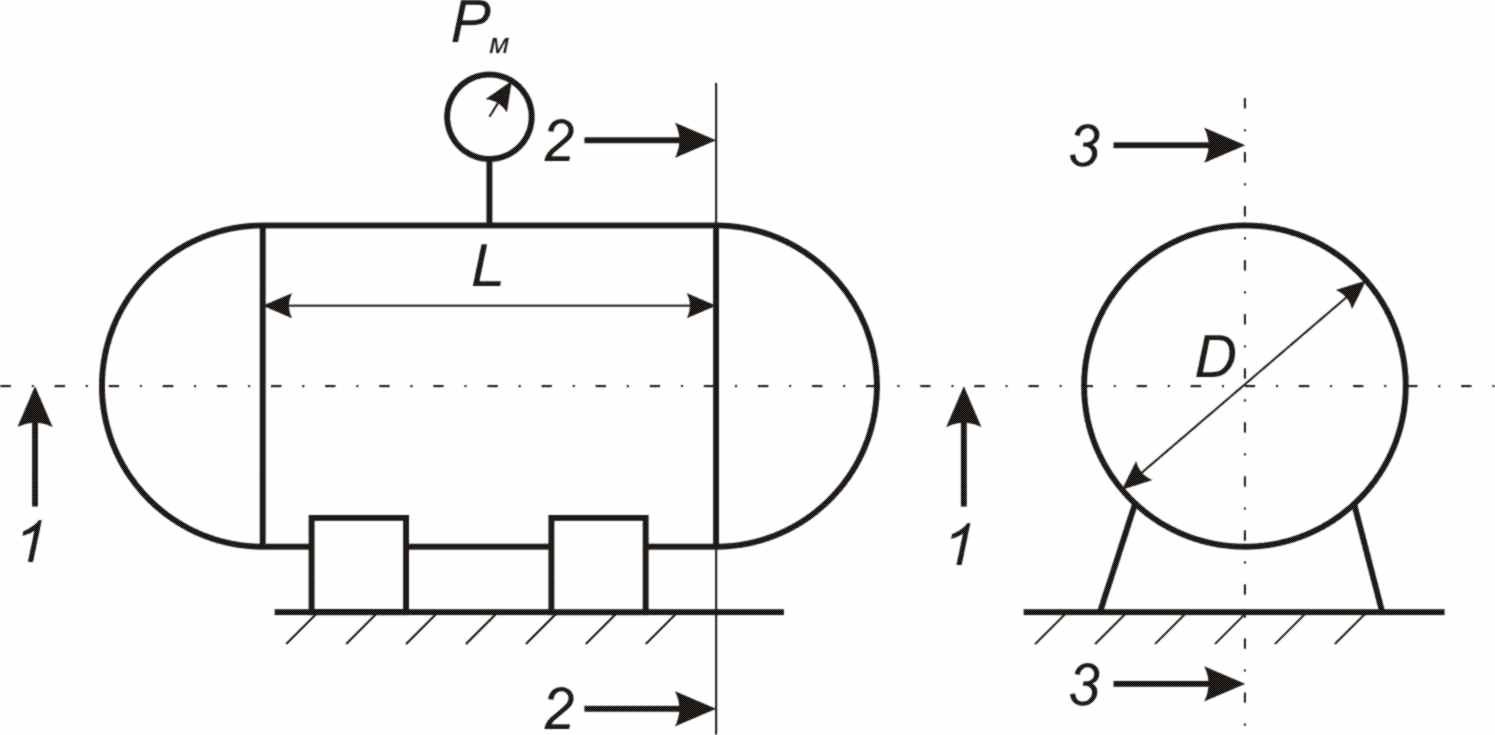
Решение: Из основного уравнения гидростатики и учитывая вертикальную составляющую силу давления, направленную противоположно (вниз): 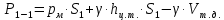 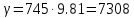 – удельный вес авиационного бензина при температуре 200 С, Н/м3; – удельный вес авиационного бензина при температуре 200 С, Н/м3;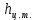 – высота центра тяжести, м; – высота центра тяжести, м; 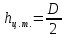 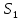 - площадь сечения цистерны в сечении 1-1, м2, - площадь сечения цистерны в сечении 1-1, м2,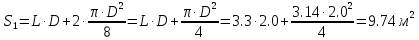 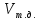 - объем тела давления, м3 - объем тела давления, м3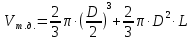 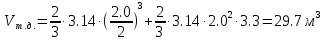 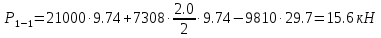 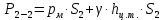 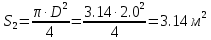 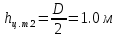 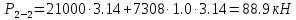 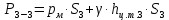 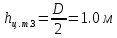 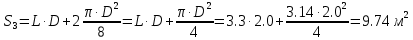 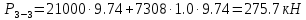 Задача 5д. Круглое отверстие между двумя резервуарами закрыто конической крышкой с размерами D и L. Закрытый резервуар заполнен водой, а открытый резервуар – жидкостью Ж. К закрытому резервуару сверху присоединен мановаккуумметр MV, показывающий манометрическое давление рман или величину вакуума рвак. Температура жидкостей 20 0С, глубины h и Н. Определить силу, срезывающую болты А, и горизонтальную силу, действующую на крышку. 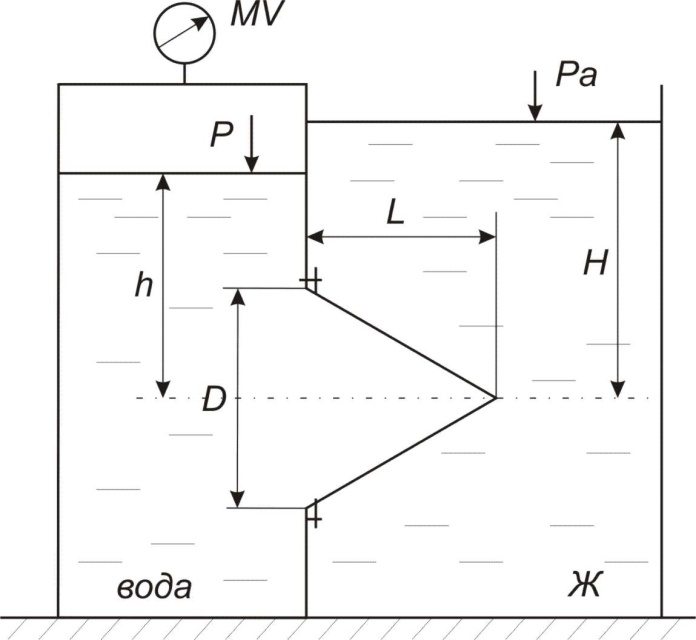
Решение: На выделенный объем жидкости в вертикальном направлении, кроме силы Fв (вертикальной силы), действуют его вес (G=V) и сила давления на свободную поверхность, равная произведению давления на площадь горизонтальной проекции поверхности АВС. Тогда вертикальная сила будет выражена: 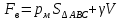 V – объем тела давления, м3 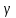 – удельный вес жидкости, (для керосина Т-2 – удельный вес жидкости, (для керосина Т-2 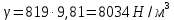 ) )Определим площадь горизонтальной проекции поверхности конуса – это треугольник: 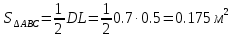 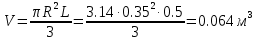 Определим вертикальную составляющую, действующую на крышку слева со стороны воды: 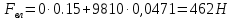 Определим вертикальную составляющую, действующую на крышку справа со стороны керосина Т-2: 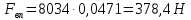 Равнодействующая сила, действующая в вертикальном направлении: 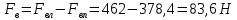 – сила, срезывающая болты. – сила, срезывающая болты.Определим горизонтальную силу. Горизонтальная составляющая силы давления жидкости на криволинейную стенку будет равна силе давления жидкости на ее вертикальную проекцию. 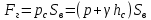 где 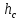 - высота центра тяжести, м (слева 2.5 м, справа 3.0 м – по исходным данным); - высота центра тяжести, м (слева 2.5 м, справа 3.0 м – по исходным данным); 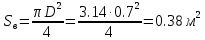 Определим горизонтальную составляющую, действующую на крышку слева со стороны воды: 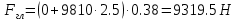 Определим горизонтальную составляющую, действующую на крышку справа со стороны дизельного топлива: 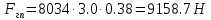 Равнодействующая сила, действующая в горизонтальном направлении: 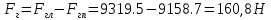 Ответ: 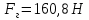 , , 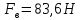 . .Задача 7е. Цилиндрический резервуар заполнен жидкостью Ж до высоты ¾ Н. диаметр резервуара D, температура жидкости 200С. Определить: Объем жидкости, сливающийся из резервуара при его вращении с частотой n об/мин вокруг его вертикальной оси; Силу давления на дно резервуара и горизонтальную силу, разрывающую резервуар по сечению 1 – 1 при его вращении.
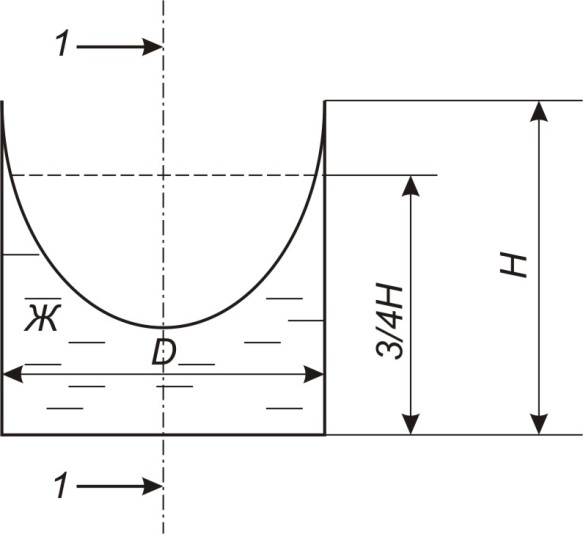 Решение: Определим угловую скорость: 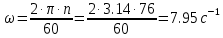 Сила давления жидкости на дно резервуара при вращении: 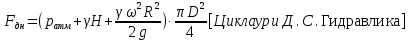 ратм – атмосферное давление, 105 Па; 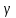 - удельный вес жидкости, - удельный вес жидкости, 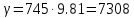 – удельный вес авиационного бензина при температуре 20о С, Н/м3; – удельный вес авиационного бензина при температуре 20о С, Н/м3;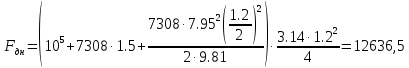 Определим объем жидкости, сливающейся из резервуара при его вращении. Для этого необходимо найти наибольшую разницу уравнений между наименьшей точкой свободной поверхности в центре и наивысшей у боковой стенки по формуле: 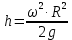 - высота параболоида вращения (при вращении жидкости вместе с цилиндрическим сосудом относительно вертикальной оси симметрии с постоянной угловой скоростью, ее поверхность под действием центробежных сил вращения принимает форму параболоида вращения). - высота параболоида вращения (при вращении жидкости вместе с цилиндрическим сосудом относительно вертикальной оси симметрии с постоянной угловой скоростью, ее поверхность под действием центробежных сил вращения принимает форму параболоида вращения).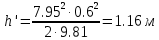 Объем параболоида: 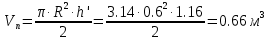 Объем жидкости в резервуаре в состоянии покоя: 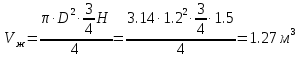 Объем резервуара: 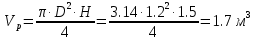 Объем жидкости в резервуаре при вращении: 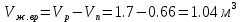 Объем сливающейся жидкости в резервуаре при вращении: 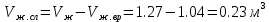 Горизонтальная сила, разрывающая резервуар по сечению 1–1: 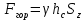 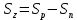 - площадь вертикальной проекции жидкости, м2 - площадь вертикальной проекции жидкости, м2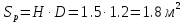 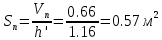 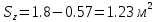 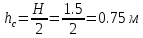 - высота центра тяжести. - высота центра тяжести.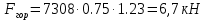 КОНТРОЛЬНАЯ РАБОТА №2 Задача 12г. Из большого открытого резервуара А, в котором поддерживается постоянный уровень жидкости, по трубопроводу, состоящему из двух последовательно соединенных трубопроводов, изготовленных из материала сталь нержавеющая, жидкость Ж при температуре 200С течет в резервуар Б. Разность уровней жидкости в резервуарах А и Б равна Н. Длина труб lи l2, а их диаметры dиd2, Определить расход жидкости, протекающей по трубопроводам 1 и 2. В расчетах принять, что местные потери напора составляют 15% от потерь по длине. 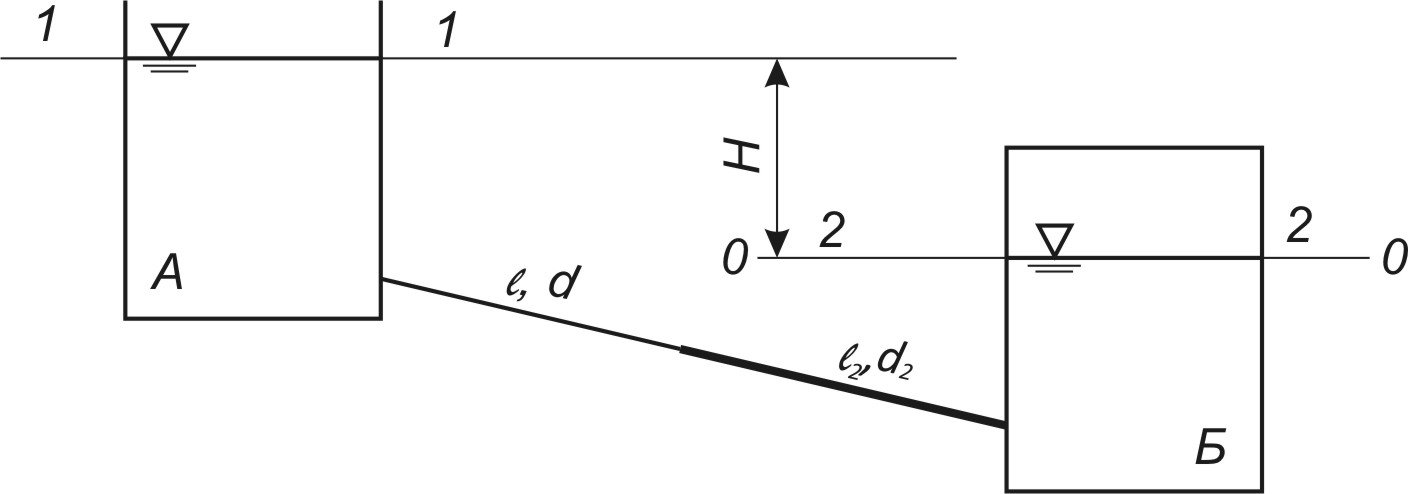
Решение: Потери напора в каждом из трубопроводов будут складываться из местных потерь и потерь по длине, которые можно определять по формуле Дарси-Вейсбаха: 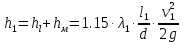 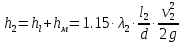 Расходом жидкости называется ее количество, проходящее в единицу времени через живое сечение. 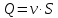 , где v – скорость жидкости в трубопроводе, S – площадь сечения трубопровода: , где v – скорость жидкости в трубопроводе, S – площадь сечения трубопровода: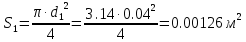 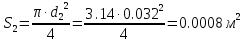 Чтобы найти скорость, составим уравнение Бернулли для сечения 1-1 и 2-2 относительно плоскости сравнения 0-0. В общем виде: 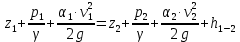 z – геометрическая высота, или геометрический напор; р/=р/g - пьезометрическая высота или пьезометрический напор (отвечает гидродинамическому давлению); v2/2g – скоростная высота или скоростной напор; h1-2 – потери по длине (местными потерями пренебрегаем). – безразмерный коэффициент Кориолиса, учитывающий неравномерность распределения скоростей. Представляет собой отношение действительной кинетической энергии потока жидкости в данном сечении, протекающем в единицу времени к теоретической кинетической энергии (принимаем =1). Для нашего случая: z1=Н, z2=0 (так как ось 0-0 проходит через центр тяжести сечения 2-2); р1=р2=ратм; v1= v2=0 (скорость на поверхности жидкости в резервуаре 0). 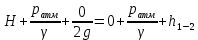 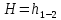 (1) (1)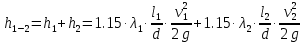 где - коэффициент гидравлического сопротивления, коэффициент можно определить по формуле Б. Л. Шифринсона: 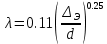 , Э – эквивалентная шероховатость, для стали Э =0.070 мм, то есть: , Э – эквивалентная шероховатость, для стали Э =0.070 мм, то есть: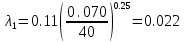 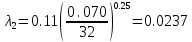 Формула (1) примет вид: 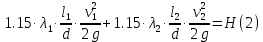 Используя уравнение неразрывности: 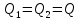 , то есть , то есть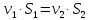 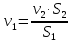 Поставим выражение (3) в (2): 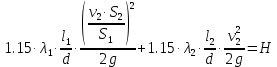 Найдем отсюда скорость v2: 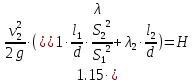 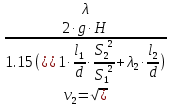 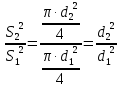 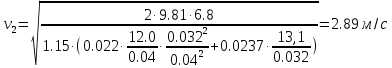 Определим расход: 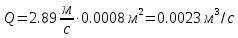 Ответ: Q=0.0023 м3/с Задача 14д. Определить расход жидкости Ж, температура которой 200 С, протекающей по трубопроводу в пункты 1 и 2, если напор Н в резервуаре А постоянный. Длины отдельных частей трубопровода (э=0,020 мм) соответственно равны l, l1, l2, а диаметры d, d1, d2. Местные потери напора в расчетах не учитывать.
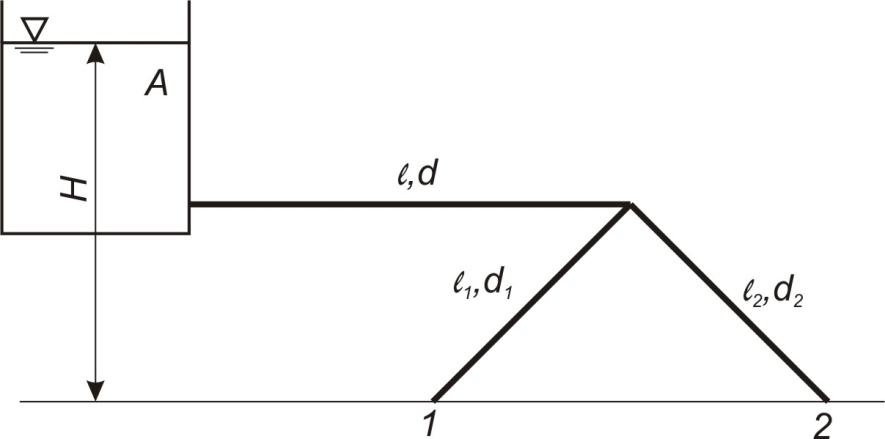 Решение: Потери напора Нпот=Н. На участке длиной l : 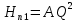 На участке длиной l1: 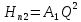 На участке длиной l2: 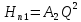 где А, А1, А2 – сопротивления трубопроводов. Общие потери напора при параллельном соединении трубопроводов: 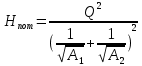 При последовательно-параллельном соединении трубопроводов потери напора определяются по формуле: 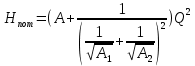 Сопротивление отдельных простых трубопроводов определим по формуле: 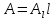 где Аl – удельное сопротивление трубопровода по длине. 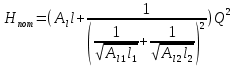 Выразим расход: 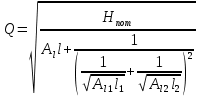 Al, Al1, Al2 – из табл. 10 Я.Н. Флексер «Практикум по гидравлике». В зависимости от d, шероховатости и материала в трубы: Аl=44530 с2/м6 Аl1= Аl2=93860 с2/м6 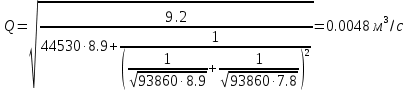 Ответ: Q=0.0048 м3/с Задача 16е. Жидкость Ж в количестве Q по горизонтальной трубе вытекает из большого резервуара А. Определить ударное повышение давления и напряжения в стенках трубы перед задвижкой К при ее внезапном закрытии. Диаметр трубы d1, ее длина l1, а толщина стенок . Материал трубы М.
По формуле Жуковского можно определить повышение давления при гидравлическом ударе 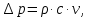 где - плотность жидкости, с – скорость с которой распространяется волна, v – скорость движения жидкости до закрытия задвижки. Величина скорости распространения ударов волны зависит от рода жидкости, материала и размеров трубы и определяется по формуле: 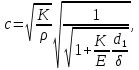 где К – модуль упругости жидкости (для воды 2,06109 Па); Е – модуль упругости материала трубы(для черного чугуна 152109 Па); d1 – диаметр трубы; – толщина стенки трубы. Определим скорости: 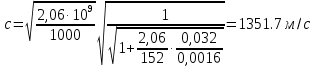 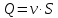 , где v – скорость жидкости в трубопроводе, S – площадь сечения трубопровода: , где v – скорость жидкости в трубопроводе, S – площадь сечения трубопровода: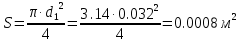 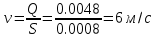 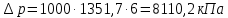 Напряжение в стенках трубопровода: 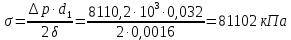 Ответ: 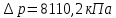 ; ; 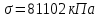 . . |
