Контроша, для Дашки. Контрольная работа по курсу Теория преобразования и передачи измерительной информации
 Скачать 331 Kb. Скачать 331 Kb.
|
|
Министерство образования республики Беларусь Учреждение образования «БЕЛОРУССКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ИНФОРМАТИКИ И РАДИОЭЛЕКТРОНИКИ» Институт информационных технологий Специальность «Программное обеспечение информационных технологий» КОНТРОЛЬНАЯ РАБОТА По курсу «Теория преобразования и передачи измерительной информации» Вариант № 4 Студент-заочник 2 курса Группы №181022 ФИО Дарья Адрес: Тел: Минск, 2012 Задание 1. С использованием алгоритмов Хаффмана и Шеннона - Фэно произвести эффективное кодирование данного сообщения: «Проверочные биты». При кодировании распределение вероятностей различных букв сообщения определить из анализа сообщения. Эффективное кодирование с использованием алгоритма Хаффмана: Дано сообщение «Преобразование сообщений», отсюда следует, что символов 13: «Пробел», Б, В, Е, И, Н, О, П, Р, Т, Ч, Ы с вероятностями: Построим дерево Хаффмана, для данного сообщения. 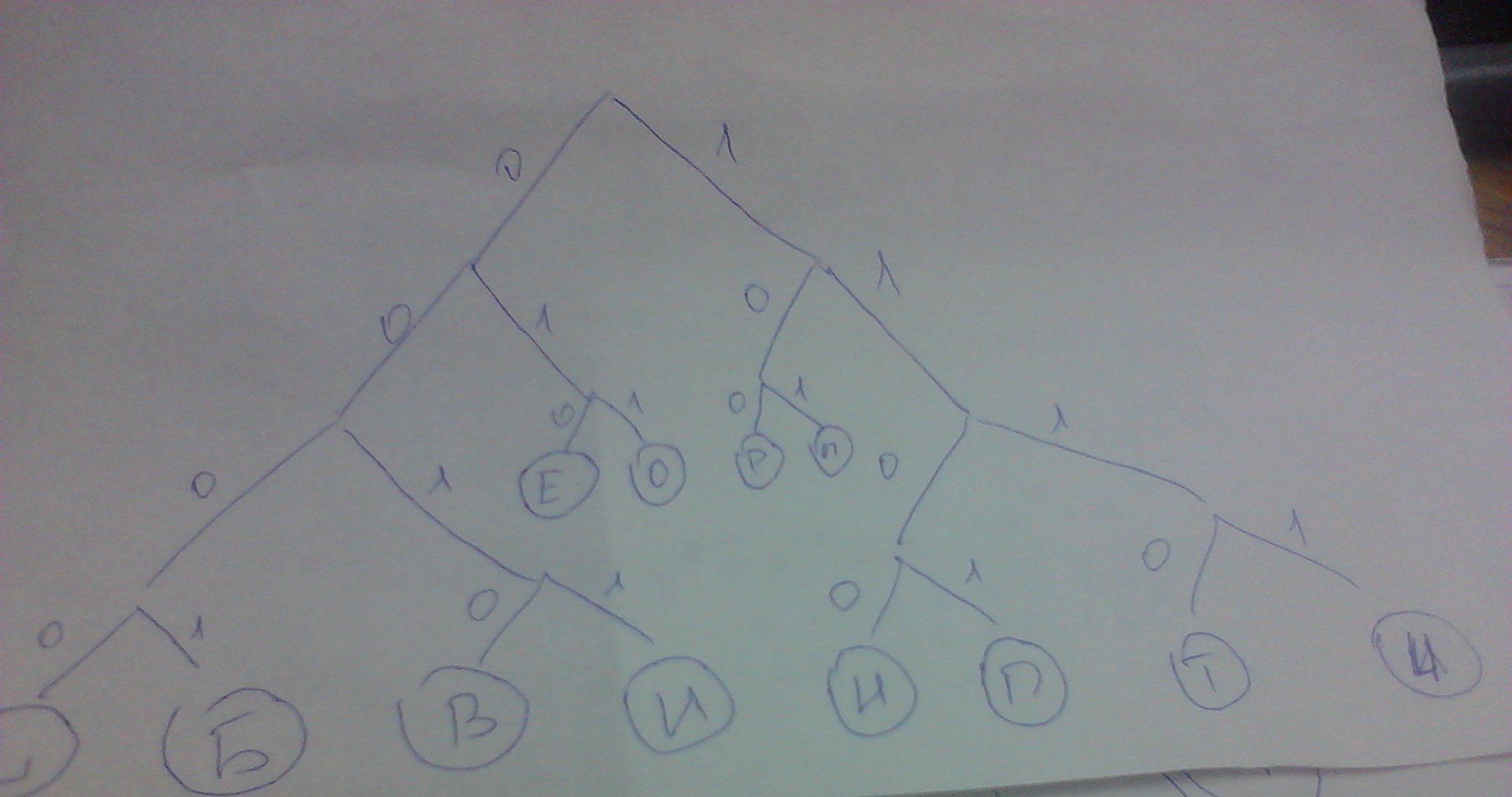   Пробел Ч По методике Хаффмана, это сообщение будет выглядеть следующим образом: 11011000110010010100011111111001010100000000100111110101 Эффективное кодирование с использованием алгоритма Шеннона – Фэно: По этой методике код строится следующим образом. Буквы алфавита сообщений выписываются в таблицу в порядке убывания вероятностей. Затем они разделяются на две группы так, чтобы суммы вероятностей в каждой из групп были по возможности одинаковы. Всем буквам верхней половины в качестве первого символа приписывается 1, а всем нижним – 0. Каждая из полученных групп разбивается на две подгруппы с одинаковыми суммарными вероятностями и т. д. Процесс повторяется до тех пор, пока в каждой подгруппе останется по одной букве.
Для получения таким образом кода среднее число двоичных символов, приходящихся на одну букву, равно: 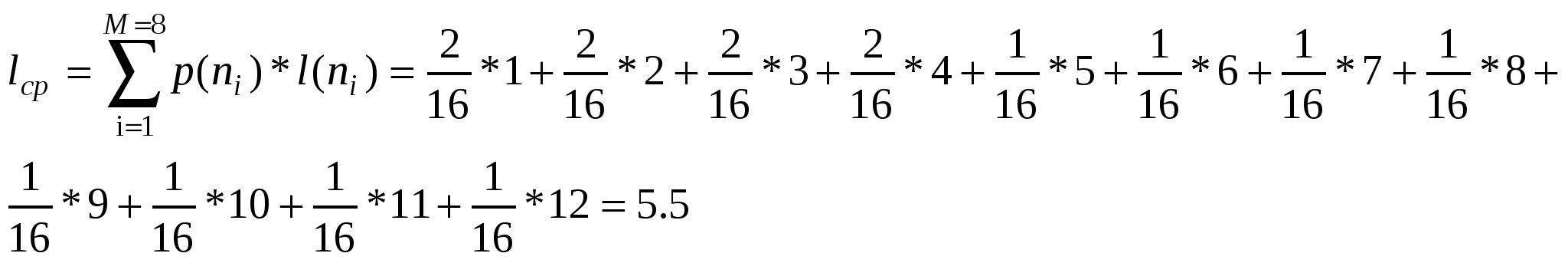 По методике Шеннона – Фэно, это сообщение будет выглядеть следующим образом: 11010100011010000010111111000110001000100110111110011 Задание 2. Используя метод шифрования перестановками, зашифровать данное сообщение: «Преобразование сообщений», используя в качестве шаблона прямоугольник с числом столбцов 4. Шифрование проводится в следующем порядке: 1.) Шифруемый текст записывается последовательными строками под числами ключевой последовательности, образуя блок шифрования размером n*m. 2.)Зашифрованный текст выписывается колонками в порядке возрастания номеров колонок, задаваемых ключевой последовательностью. 3.)Заполняется новый блок и т.д. Блок будет размером 4*6
По шифру простой перестановки, мы получаем следующее: Шифртекст: Пенбррыиооетвч ы Широко распространена разновидность шифра маршрутной перестановки, называемая ``шифром вертикальной перестановки'' (ШВП). В нем снова используется прямоугольник, в который сообщение вписывается обычным способом (по строкам слева направо). Выписываются буквы по вертикали, а столбцы при этом берутся в порядке, определяемом ключом. По ключу мы получаем следующее: Шифртекст: ооетпенбвч ыррыи Задание 3. Используя шифрование с ключом, закодировать сообщения, используя в качестве ключа слова: Алгоритм, Разряд, Кодирование. Шифрование с ключом:
Задание 4. Дополнить по строкам и столбцам информационные двоичные блоки, проверочными битами четности.
В начале мы рассмотрим каждую строку: Число 10011 содержит 3 '1' битов. Бит чётности будет 1, получаем кодовое слово 100111; Число 10100 содержит 2 '1' битов. Бит чётности будет 0, получаем кодовое слово 101000; Число 00100 содержит 1 '1' битов. Бит чётности будет 1, получаем кодовое слово 001001; Число 11001 содержит 3 '1' битов. Бит чётности будет 1, получаем кодовое слово 110011; Теперь рассмотрим каждый столбец: Число 1101 содержит 3 '1' битов. Бит чётности будет 1, получаем кодовое слово 11011; Число 0001 содержит 1 '1' битов. Бит чётности будет 1, получаем кодовое слово 00011; Число 0110 содержит 2 '1' битов. Бит чётности будет 0, получаем кодовое слово 01100; Число 1000 содержит 1 '1' битов. Бит чётности будет 1, получаем кодовое слово 10001; Число 1001 содержит 2 '1' битов. Бит чётности будет 0, получаем кодовое слово 10010; В итоге мы получили:
Задание 5. По заданному кодирующему многочлену построить полиномиальные коды для заданных двоичных сообщений.
Полиномиальный код с кодирующим многочленом g(x) кодирует слово сообщения а(х) многочленом b(x)=a(x)g(x)= g(x)= Х7+х5+ х3+х+1. Сообщение 1001001, отвечающее многочлену а(х)=x6+x3+1 будет закодировано коэффициентами многочлена Список использованных источников:
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
