Административная контрольная работа по математике (базовый уровень) 11 класс
Вариант 1
№
|
Элементы содержания, контролируемые входной контрольной работой.
|
Критерии оценивания в баллах.
|
1.
|
Найдите корень уравнения 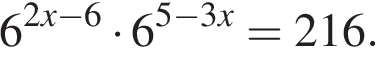
|
1
|
2.
|
Решите неравенство 
|
1
|
3.
|
Найдите значение выражения
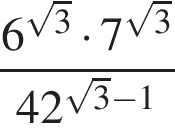
|
1
|
4.
|
На графике изображена зависимость скорости движения легкового автомобиля от времени. На вертикальной оси отмечена скорость легкового автомобиля в км/ч, на горизонтальной — время в секундах, прошедшее с начала движения автомобиля.
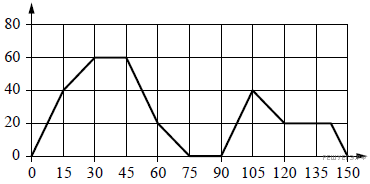
Пользуясь графиком, поставьте в соответствие каждому интервалу времени характеристику движения автомобиля на этом интервале.
ИНТЕРВАЛЫ ВРЕМЕНИ
|
|
ХАРАКТЕРИСТИКИ
|
А) 0–30 c
Б) 30–60 c
В) 90–120 c
Г) 120–150 c
|
|
1) автомобиль ехал с постоянной скоростью больше 15 секунд
2) скорость автомобиля сначала увеличивалась, а потом уменьшалась
3) автомобиль увеличивал скорость на всём интервале
4) автомобиль ровно 15 секунд ехал с постоянной скоростью
|
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
|
1
|
5.
|
Биатлонист 5 раз стреляет по мишеням. Вероятность попадания в мишень при одном выстреле равна 0,8. Найдите вероятность того, что биатлонист первые 2 раза попал в мишени, а последние три промахнулся. Результат округлите до сотых.
|
1
|
6.
|
Два велосипедиста одновременно отправились в 88-километровый пробег. Первый ехал со скоростью, на 3 км/ч большей, чем скорость второго, и прибыл к финишу на 3 часа раньше второго. Найти скорость велосипедиста, пришедшего к финишу вторым. Ответ дайте в км/ч.
|
2
|
7.
|
На клетчатой бумаге с клетками размером 1 см
 1 см изображена фигура (см. рисунок). Найдите ее площадь в квадратных сантиметрах. 1 см изображена фигура (см. рисунок). Найдите ее площадь в квадратных сантиметрах.

|
1
|
8.
|
 Центральный угол на 48° больше острого вписанного угла, опирающегося на ту же дугу окружности. Найдите вписанный угол. Ответ дайте в градусах. Центральный угол на 48° больше острого вписанного угла, опирающегося на ту же дугу окружности. Найдите вписанный угол. Ответ дайте в градусах.
|
1
|
9.
|
Длина окружности основания цилиндра 10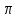 см. Диагональ осевого сечения цилиндра 13 см. Найдите высоту цилиндра. см. Диагональ осевого сечения цилиндра 13 см. Найдите высоту цилиндра.
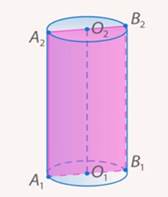
|
1
|
10
|
Найдите площадь поверхности прямой призмы, в основании которой лежит ромб с диагоналями, равными 6 и 8, и боковым ребром, равным 10.
|
1
|
11
|
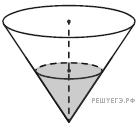 В сосуде, имеющем форму конуса, уровень жидкости достигает В сосуде, имеющем форму конуса, уровень жидкости достигает  высоты. Объём жидкости равен 90 мл. Сколько миллилитров жидкости нужно долить, чтобы наполнить сосуд доверху? высоты. Объём жидкости равен 90 мл. Сколько миллилитров жидкости нужно долить, чтобы наполнить сосуд доверху?
|
1
|
12
|
В правильной четырёхугольной призме ABCDA1B1C1D1 ребро AA1 равно 9, а диагональ BD1 равна 15. Найдите площадь сечения призмы плоскостью, проходящей через точки A, A1 и C.
|
2
|
Шкала оценивания:
Контрольная работа по пятибалльной шкале.
|
«2»
|
«3»
|
«4»
|
«5»
|
Общий балл.
|
0-6
|
7 - 9
|
10 - 12
|
13 - 14
|
Административная контрольная работа по математике (базовый уровень)
10 класс
Вариант 2
№
|
Элементы содержания, контролируемые входной контрольной работой.
|
Критерии оценивания в баллах.
|
1.
|
Найдите корень уравнения 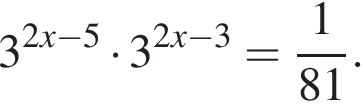
|
1
|
2.
|
Решите неравенство 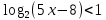
|
1
|
3.
|
Найдите значение выражения
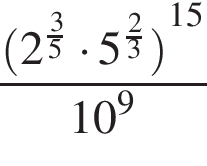
|
1
|
4.
|
На графике изображена зависимость скорости погружения батискафа от времени. На вертикальной оси отмечена скорость в м/с, на горизонтальной — время в секундах, прошедшее с начала погружения.

Пользуясь графиком, поставьте в соответствие каждому интервалу времени характеристику погружения батискафа на этом интервале.
ИНТЕРВАЛЫ
|
|
ХАРАКТЕРИСТИКИ ДВИЖЕНИЯ
|
А) 60–150 c
Б) 150–180 c
В) 180–240 c
Г) 240–300 c
|
|
1) Батискаф 45 секунд погружался с постоянной скоростью.
2) Скорость погружения уменьшалась, а затем произошла остановка на полминуты.
3) Скорость погружения достигла максимума за всё время.
4) Скорость погружения не увеличивалась на всём интервале, но батискаф не останавливался.
|
В таблице под каждой буквой укажите соответствующий номер.
|
1
|
5.
|
Биатлонист 4 раза стреляет по мишеням. Вероятность попадания в мишень при одном выстреле равна 0,85. Найдите вероятность того, что биатлонист первые 2 раза попал в мишени, а последние два промахнулся. Результат округлите до сотых.
|
1
|
6.
|
Два велосипедиста одновременно отправились в 96-километровый пробег. Первый ехал со скоростью, на 4 км/ч большей, чем скорость второго, и прибыл к финишу на 4 часа раньше второго. Найти скорость велосипедиста, пришедшего к финишу вторым. Ответ дайте в км/ч.
|
2
|
7.
|
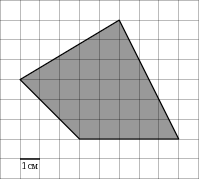
На клетчатой бумаге с клетками размером 1 см
 1 см изображена фигура (см. рисунок). Найдите ее площадь в квадратных сантиметрах. 1 см изображена фигура (см. рисунок). Найдите ее площадь в квадратных сантиметрах.
|
1
|
8.
|
 Центральный угол окружности на 36° больше вписанного угла, опирающегося на ту же дугу данной окружности. Найдите центральный угол. Ответ дайте в градусах. Центральный угол окружности на 36° больше вписанного угла, опирающегося на ту же дугу данной окружности. Найдите центральный угол. Ответ дайте в градусах.
|
1
|
9.
|

|
1
|
10
|
Найдите площадь поверхности прямой призмы, в основании которой лежит ромб с диагоналями, равными 9 и 12, и боковым ребром, равным 5.
|
1
|
11
|
 В цилиндрическом сосуде уровень жидкости достигает 16 см. На какой высоте будет находиться уровень жидкости, если ее перелить во второй сосуд, диаметр которого в В цилиндрическом сосуде уровень жидкости достигает 16 см. На какой высоте будет находиться уровень жидкости, если ее перелить во второй сосуд, диаметр которого в 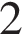 раза больше первого? Ответ выразите в см. раза больше первого? Ответ выразите в см.
|
1
|
12
|
В правильной треугольной призме ABCA1B1C1 стороны оснований равны 2, боковые рёбра равны 5. Найдите площадь сечения призмы плоскостью, проходящей через середины рёбер AB, AC, A1B1 и A1C1
|
2
|
Шкала оценивания:
Контрольная работа по пятибалльной шкале.
|
«2»
|
«3»
|
«4»
|
«5»
|
Общий балл.
|
0-6
|
7 - 9
|
10 - 12
|
13 - 14
| |
 Скачать 108.86 Kb.
Скачать 108.86 Kb.



 Центральный угол на 48°
Центральный угол на 48° 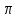 см. Диагональ осевого сечения цилиндра 13 см. Найдите высоту цилиндра.
см. Диагональ осевого сечения цилиндра 13 см. Найдите высоту цилиндра.
 В сосуде, имеющем форму конуса, уровень жидкости достигает
В сосуде, имеющем форму конуса, уровень жидкости достигает 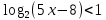
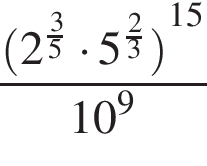


 Центральный угол окружности на 36° больше вписанного угла, опирающегося на ту же дугу данной окружности. Найдите центральный угол. Ответ дайте в градусах.
Центральный угол окружности на 36° больше вписанного угла, опирающегося на ту же дугу данной окружности. Найдите центральный угол. Ответ дайте в градусах.
 В цилиндрическом сосуде уровень жидкости достигает 16 см. На какой высоте будет находиться уровень жидкости, если ее перелить во второй сосуд, диаметр которого в
В цилиндрическом сосуде уровень жидкости достигает 16 см. На какой высоте будет находиться уровень жидкости, если ее перелить во второй сосуд, диаметр которого в