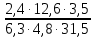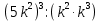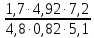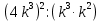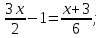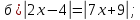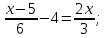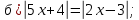|
|
Итоговая работа по математике 7 класс. МОЯ Итоговая контрольная работа по математике за курс 7 класса. Контрольная работа по математике за курс 7 класса. Вариант 1 Вариант 2 Часть А
Итоговая контрольная работа по математике за курс 7 класса.
Вариант 1
|
Вариант 2
|
Часть А
|
Часть А
|
1.(1б.) Вычислите
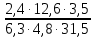
2.(1б.) Упростите выражение: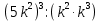
3.(2б.) Решите уравнения: а) 18-3(х-5)2= - 3х2-15;
б) 3х2-2х=0.
4. (2б.) Постройте график функции у= - 0,4х+5. Принадлежите ли графику данной функции
т.М(-200;10)?
5.(2б.) Один из внутренних односторонних углов при параллельных прямых m и n и секущей k в 5 раз больше другого. Найдите эти углы.
6.(2б.) Решите задачу с помощью системы уравнений:
Сумма двух чисел равна 81, а из разность равна 15. Найдите большее из этих чисел.
|
1.(1б.) Вычислите
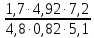
2.(1б.)Упростите выражение: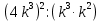
3.(2б.)Решите уравнения: а) 15-7(3-х)2= - 7х2+6;
б) 5х2-2х=0.
4.(2б.) Постройте график функции у= - 0,6х+4. Принадлежите ли графику данной функции
т.Р(-100;20)?
5.(2б.) Один из внутренних односторонних углов при параллельных прямых d и g и секущей t в 4 раз больше другого. Найдите эти углы.
6.(2б.) Решите задачу с помощью системы уравнений:
Сумма двух чисел равна 73, а из разность равна 19. Найдите меньшее из этих чисел.
|
Часть В
|
Часть В
|
1.(3б.) Разложите на множители: а) 36a4-25a2b2;
b) (x-7)2-81; c) a3-8b3.
2.(2б.) Решите уравнения: а) 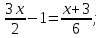
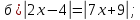
3.(2б.) График линейной функции проходит через точки А(3; 1) и В(2; -2). Постройте график и задайте функцию формулой.
4.(3б.) Отрезок АВ является хордой окружности с центром О. Найдите угол между прямой АВ и касательной к окружности, проходящей через точку А, если угол АОВ равен 28°.
5*.(5б.) Каждый житель острова Сонный просыпается всегда одним и тем же способом. Способов всего три:
(А) открыть одновременно оба глаза и бежать на зарядку
(Б) открыть сначала левый глаз, а через 16 минут — правый, и бежать на завтрак
(В) открыть сначала правый глаз, а через 27 минут — левый.
В социологическом опросе службы "Доброе утро" приняли участие жители городов Кривдина и Правдина, всего 1024 островитянина.
Каждому было задано по 3 вопроса:
(1) "Просыпаетесь ли Вы способом А?"
(2) "Просыпаетесь ли Вы способом Б?"
(3) "Просыпаетесь ли Вы способом В?"
Ответов "Да" на первый вопрос было 289, на второй вопрос — 361, на третий вопрос — 441.
Сколько жителей каждого из городов приняло участие в опросе?
|
1.(3б.) Разложите на множители: a) 4x2y2-9a4;
b) 25-(a+3)2; c) 27m3+n3.
2.(2б.) Решите уравнения: а) 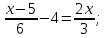
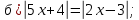
3.(2б.) График линейной функции проходит через точки А(2; -1) и В(1; 3). Постройте график и задайте функцию формулой.
4.(3б.) Отрезок АВ является хордой окружности с центром О. Найдите угол АОВ, если угол между прямой АВ и касательной к окружности, проходящей через точку А, равен 37°.
5*.(5б.) Кот Матроскин и пес Шарик каждое утро бегают на речку умываться. Они выскакивают из дома одновременно и бегут по одной и той же тропинке. Скорость каждого из них постоянна, но Матроскин бежит в 3 раза быстрее Шарика, зато моется в 2 раза дольше, чем Шарик. Однажды Шарик, прибежав к речке, обнаружил, что не взял с собой полотенце. Он тут же побежал домой, схватил полотенце и прибежал к речке как раз в тот момент, когда Матроскин закончил умываться (бежал Шарик по той же тропинке и с той же скоростью, что и каждое утро).
Кто обычно прибегает домой раньше – Шарик или Матроскин или они прибегают домой одновременно?
|
Решение: Для каждого человека подходит только один вариант ответа, а два не подходят.
Поэтому житель города Правдина должен один раз ответить "Да" и два раза "Нет", а житель города Кривдина, наоборот, один раз "Нет" и два раза "Да".
Таким образом, если бы все участники опроса были из Правдина, то ответов "Да" было бы столько же, сколько и участников, то есть, 1024.
Каждый житель Кривдина даёт два ответа "Да", добавляя один лишний ответ.
Всего ответов "Да" было 289 + 361 + 441 = 1091.
Значит, жителей Кривдина было 1091 - 1024 = 67. А жителей Правдина 1024 - 67 = 957.
Ответ: 957 жителей Правдина и 91 житель Кривдина.
Решение задачи 3.
Разделим дорогу от дома к речке на три участка одинаковой длины (см. рисунок) и эту длину примем за 1.

Введем новую единицу измерения – «шарик»; по определению, 1 «шарик» – это время, нужное Шарику, чтобы утром по дороге на речку пробежать участок длины 1.
По условию, когда Матроскин добегает до D (начинает умываться), Шарик как раз находится в точке B (ведь он бежит в 3 раза медленнее Матроскина). Следовательно, на дорогу от дома до речки (так же, как и на обратную дорогу) Матроскин затрачивает столько же времени, сколько нужно Шарику, чтобы пробежать отрезок длины 1, т. е. 1 «шарик».
Матроскин умывается 8 «шариков» (действительно, в тот день, когда Шарик забыл полотенце, он, как всегда, добежал до точки B, а Матроскин в этот момент начал умываться, затем Шарик пробежал 8 раз отрезок длины 1: от B к D (два участка длины 1), от D к A(три участка длины 1) и, наконец, от A к D уже с полотенцем (три участка длины 1), - и как раз Матроскин в этот момент умываться закончил). Далее, так как по условию Матроскин моется в два раза дольше Шарика, то Шарик моется 4 «шарика».
Остается подсчитать время, затраченное каждым из наших героев на дорогу от дома к речке, умывание и дорогу обратно, от речки к дому. Шарик: 3 + 4 + 3 = 10 «шариков»; Матроскин: 1 + 8 + 1 = 10 «шариков».
Следовательно, Матроскин и Шарик прибегают домой после умывания одновременно. |
|
|
 Скачать 20.09 Kb.
Скачать 20.09 Kb.