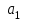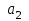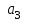тест ответы синергия. Коротаева - (в.6). Контрольная работа по предмету Математика
 Скачать 89.85 Kb. Скачать 89.85 Kb.
|
|
Контрольная работа по предмету «Математика» I семестр Задание 1. Построить экономико-математическую модель задачи. Предприятие выпускает три вида продукции, используя сырье трех видов. Расходы сырья задаются матрицей A=(aij), где aij – это расход i-го сырья на 1ед. продукции j-го вида. Запасы сырья задаются матрицей Q=(qi), где qi – запас сырья i-го вида. Определить объем выпуска продукции каждого вида при заданных запасах сырья. Исходные данные приведены ниже в соответствующих таблицах (первые три столбца – матрица A, четвертый – матрица Q). Систему решить матричным способом и методом Крамера.
Решение: Запишем экономико-математическую модель задачи: 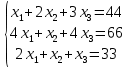 Решение. Матричный способ Обозначим через А — матрицу коэффициентов при неизвестных; X — матрицу-столбец неизвестных; B - матрицу-столбец свободных членов: 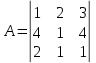 , , 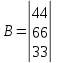 С учетом этих обозначений данная система уравнений принимает следующую матричную форму: А*Х = B. Если матрица А — невырожденная (ее определитель отличен от нуля, то она имеет обратную матрицу А-1. Умножив обе части уравнения на А-1, получим: А-1*А*Х = А-1*B, А-1*А=Е. Это равенство называется матричной записью решения системы линейных уравнений. Для нахождения решения системы уравнений необходимо вычислить обратную матрицу А-1. Система будет иметь решение, если определитель матрицы A отличен от нуля. Найдем главный определитель. 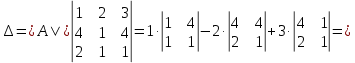 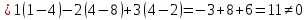 Вычисляем алгебраические дополнения элементов матрицы А 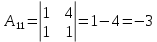 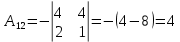 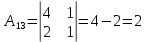 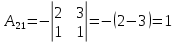 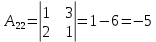 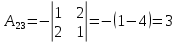 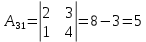 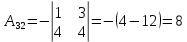 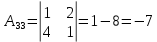 Составляем матрицу 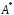 : :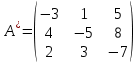 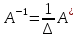  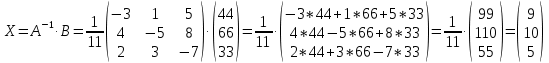 Ответ:  2. Найдем решение системы уравнений методом Крамера. Формулы Крамера: 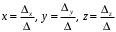 , где , где 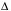 - определитель системы, - определитель системы, 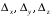 - определители, полученные из определителя системы заменой, соответственно, первого, второго и третьего столбцов на столбец свободных членов. - определители, полученные из определителя системы заменой, соответственно, первого, второго и третьего столбцов на столбец свободных членов. Вычислим определители, раскрывая их по первой строке. 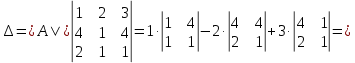 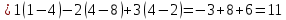 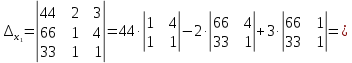 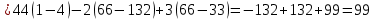 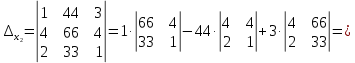 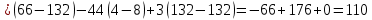 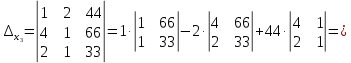 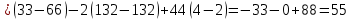 Таким образом, по формулам Крамера 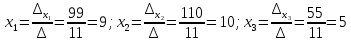 Ответ:  Задание 2. Исследовать на совместность и, в случае совместности, решить 3 системы линейных алгебраических уравнений методом Гаусса (в таблицах даны элементы расширенных матриц систем 4-х уравнений с 4-мя неизвестными):
Решение: а) 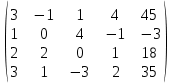 Найдем ранг расширенной матрицы системы и ранг матрицы системы. Для этого составим расширенную матрицу системы и приведём её к треугольному виду, применяя элементарные преобразования к строкам матрицы. Поменяем местами 1-ю и 2-ю строки.   Ранг основной и расширенной матриц равны rang=4, следовательно, система совместна. 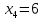 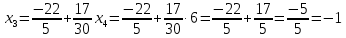 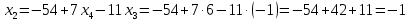 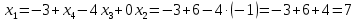 Ответ: 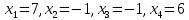 б) 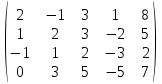 Найдем ранг расширенной матрицы системы и ранг матрицы системы. Для этого составим расширенную матрицу системы и приведём её к треугольному виду, применяя элементарные преобразования к строкам матрицы. Поменяем местами 1-ю и 2-ю строки. 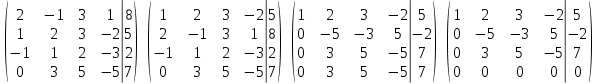 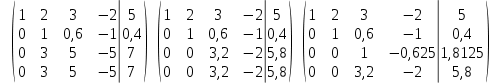 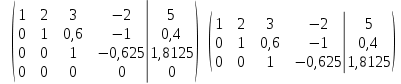 Ранг расширенной матрицы равен рангу матрицы системы rang=3, но меньше числа неизвестных, отсюда следует, что система совместна и имеет бесконечно много решений. 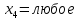 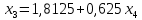 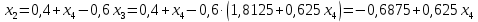 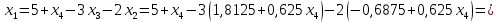 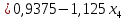 Ответ: 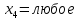 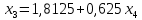 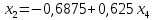  в) 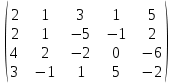 Найдем ранг расширенной матрицы системы и ранг матрицы системы. Для этого составим расширенную матрицу системы и приведём её к треугольному виду, применяя элементарные преобразования к строкам матрицы. Поменяем местами 1-й и 2-й столбцы.  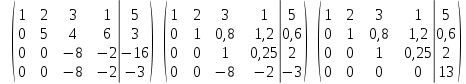 Ранг расширенной матрицы (rang=4) не равен рангу матрицы системы (rang=3), поэтому система несовместна (не имеет решений). Ответ: система несовместна, нет решений Задание 3. Заданы координаты вершин пирамиды АВСD. Требуется: Записать векторы 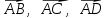 в системе орт в системе орт 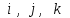 ; ;Найти угол между векторами 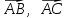 ; ;Найти проекцию вектора 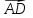 на вектор на вектор 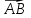 ; ;Найти площадь грани АВС; Найти объем пирамиды АВСD; Найти длину высоты DH пирамиды, опущенной из вершины D на основание АВС. A(1;2;1), B(-1;5;1), C(-1;2;7), D(1;5;9) Решение: Запишем векторы 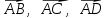 в системе орт в системе орт 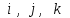 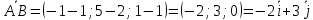 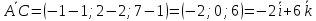 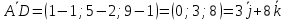 Найдем угол между векторами 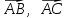 ; ;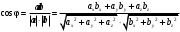 В нашем случае 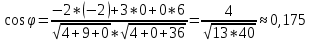 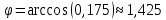 Найдем проекцию вектора 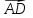 на вектор на вектор 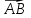 ; ;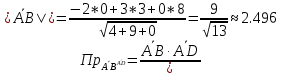 Найдем площадь грани АВС; 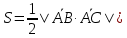 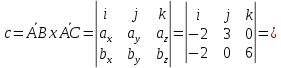  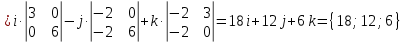 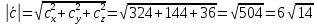 Найдем площадь треугольника. 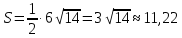 кв. ед. кв. ед.Найдем объем пирамиды АВСD; Для нахождения объема пирамиды надо найти объем параллелепипеда, построенного на гранях АВ, АС и АD и поделить его на 6. Объем этого параллелепипеда равен модулю векторного произведения векторов AB, AC и AD 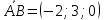 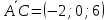 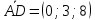 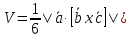 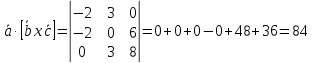 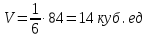 Найдем длину высоты DH пирамиды, опущенной из вершины D на основание АВС. Найдем уравнение плоскости ABC. Уравнение плоскости, проходящей через точки 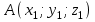 , , 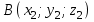 , , 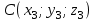 имеет вид: имеет вид: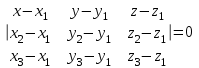 Тогда уравнение плоскости ABC в имеет вид^ 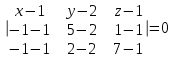 или или 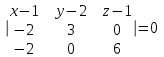 . . 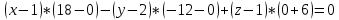 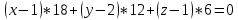 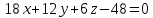 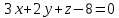 Для вычисления расстояния от точки D (1;5;9) до плоскости ABC применим формулу: 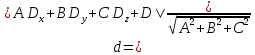 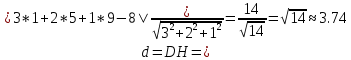 Ответ: 1) 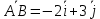 ; ; 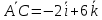 ; ; 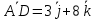 2) 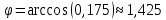 3) 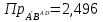 4) 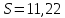 кв. ед. кв. ед.5) 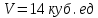 6) 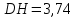 Задание 4. Даны координаты векторов  , ,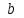 . Найти разложение . Найти разложение 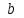 по векторам по векторам  . .
Решение: Для разложения вектора по базису запишем векторное уравнение: 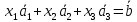 Перепишем векторное уравнение в матричном виде 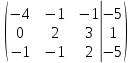 Проверим образуют ли заданные вектора базис, для этого найдем определитель матрицы: 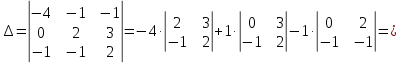  Так как определитель матрицы не равен нулю, то система векторов является базисом. Решим уравнение методом Гаусса. Разделим последнюю строку на -1 и поменяем ее местами с 1-й строкой. 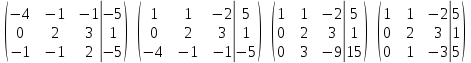 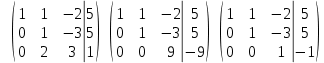 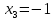 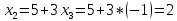 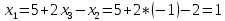 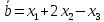 Ответ: 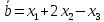 Задание 5. Даны вершины треугольника АВС. Координаты точек A,B и C заданы в таблице. Найти: 1) длину стороны АВ; 2) уравнения сторон АВ и АС и их угловые коэффициенты; 3) внутренний угол А в радианах с точностью до 0,01; 4) уравнение высоты CD и ее длину ; 5) уравнение медианы АЕ и ее длину; Построить чертеж.
Решение: 1) Найдем длину стороны АВ 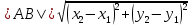 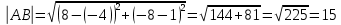 2) Найдем уравнения сторон АВ и АС и их угловые коэффициенты Уравнение прямой, проходящей через точки 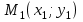 и и 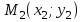 , имеет вид , имеет вид 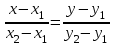 Составим уравнение АВ. По условию А(-4;1), В(8;-8). Подставим координаты точек А и В в уравнение: 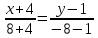 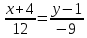 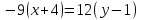 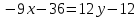 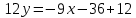 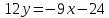 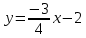 - уравнение АВ, угловой коэффициент k = -3/4. - уравнение АВ, угловой коэффициент k = -3/4.Составим уравнение АС. По условию А(-4;1), С(6;6). Подставим координаты точек А и С в уравнение: 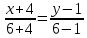 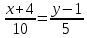  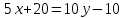 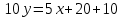 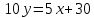 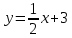 - уравнение АС, угловой коэффициент k = 1/2. - уравнение АС, угловой коэффициент k = 1/2.3) Найдем внутренний угол А в радианах с точностью до 0,01 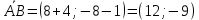 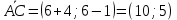 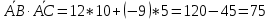 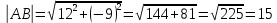 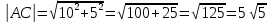 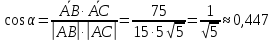  4) Найдем уравнение высоты CD и ее длину Используем уравнение прямой на плоскости, проходящей через данную точку (C) с данным нормальным вектором (AB): 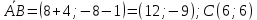 Тогда искомое уравнение: 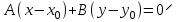 , , т.е. 12 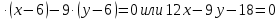 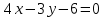 – уравнение высоты CD – уравнение высоты CDДлину высоты найдем по формуле: 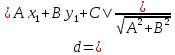 – расстояние от точки C до прямой AB – расстояние от точки C до прямой ABAB: 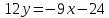 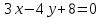 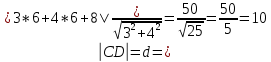 5) Найдем уравнение медианы АЕ и ее длину Обозначим середину стороны BC буквой E. Тогда координаты точки E найдем по формулам деления отрезка пополам. 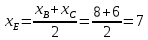 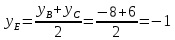 E(7;-1) E(7;-1)Уравнение медианы AE найдем, используя формулу для уравнения прямой, проходящей через две заданные точки. Медиана AE проходит через точки A(-4;1) и E(7;-1), поэтому: Каноническое уравнение прямой: 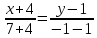 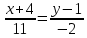 Получаем 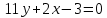 – уравнение медианы AE. – уравнение медианы AE.Найдем длину медианы. Расстояние между двумя точками выражается через координаты формулой: 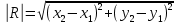 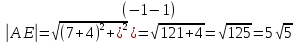 Ответ:_1)'>Ответ: 1) 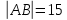 2) 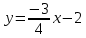 - уравнение АВ, угловой коэффициент k = -3/4; - уравнение АВ, угловой коэффициент k = -3/4; 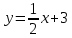 - уравнение АС, угловой коэффициент k = 1/2. - уравнение АС, угловой коэффициент k = 1/2.3)  4) 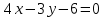 – уравнение высоты CD, – уравнение высоты CD, 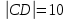 5) 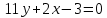 – уравнение медианы AE, – уравнение медианы AE, 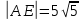 Задание 6. Найти указанные пределы 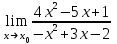 ; а) х0 = - 1; б) х0 = 1; в) х0 = . ; а) х0 = - 1; б) х0 = 1; в) х0 = .Решение: а) х0 = - 1 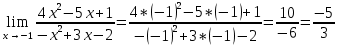 б) х0 = 1 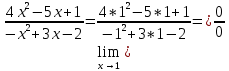 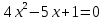 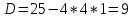 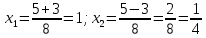  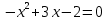 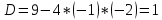 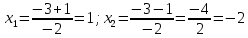 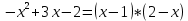 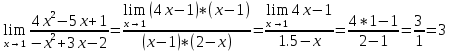 в) х0 = 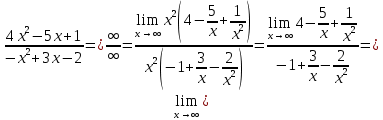 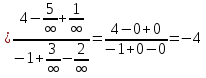 Ответ: а) -5/3, б) 3, в) -4 |