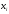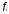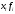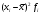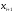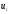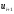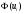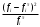Контрольная ПСК 2020. Клочков С.А. МТЗ-301. Контрольная работа по предмету Программные статистические комплексы
 Скачать 403.41 Kb. Скачать 403.41 Kb.
|
 Определим ширину интервала: 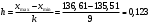 С помощью функции ЧАСТОТА в Excel определяем частоту каждого интервала (табл. 2). Таблица 2
Так как в последнем интервале меньше 5 значений, объединяем два последних интервала (табл. 3). Таблица 3
1. По сгруппированным данным находим математическое ожидание случайной величины: 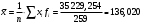 2. Рассчитаем дисперсию по сгруппированным данным: 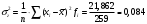 Тогда среднеквадратичное отклонение составит 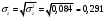 . .Рассчитаем дисперсию для выборочных данных (первые 100 значений) с помощью функции ДИСПР (рис. 1). 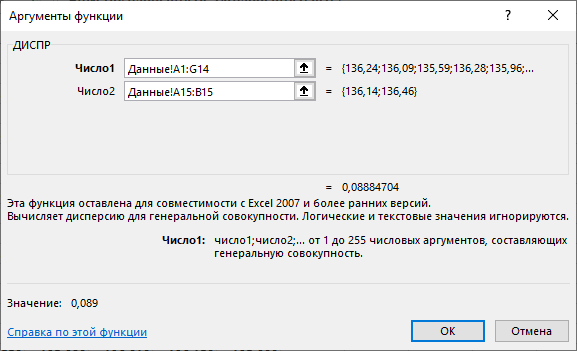 Рис. 1. Выборочная дисперсия Таким образом, выборочная дисперсия будет равна 0,089, а среднее квадратическое отклонение составит 0,298. 3. Построим гистограмму или полигон распределения значений случайной величины (рис. 2-3). 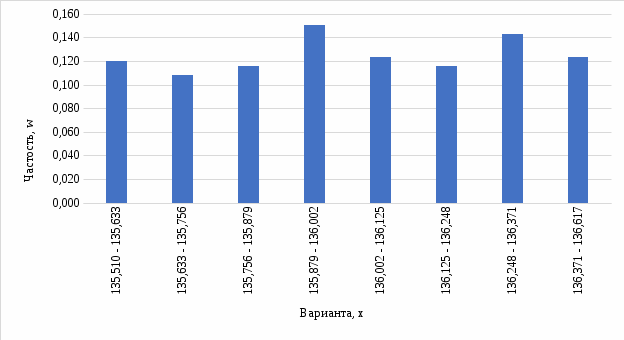 Рис. 2. Гистограмма распределения 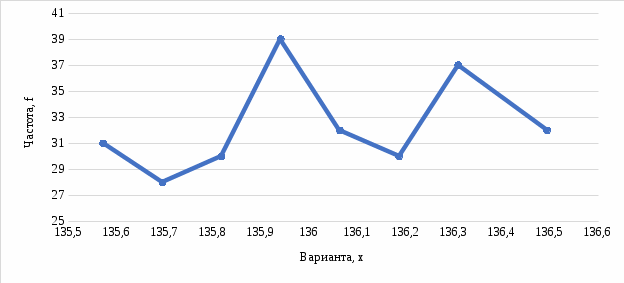 Рис. 3. Полигон распределения 4. Выдвинем гипотезу H0: распределение генеральной совокупности X подчинено нормальному закону с параметрами 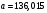 и и 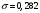 . Проверим эту гипотезу по критерию Пирсона при уровне значимости . Проверим эту гипотезу по критерию Пирсона при уровне значимости 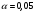 . . Рассчитываем теоретические частоты 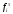 для интервала для интервала 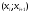 по формуле: по формуле: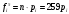 , ,где 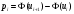 , , 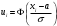 . .Значения нормального закона распределения 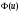 будем рассчитывать с помощью функции Excel НОРМ.СТ.РАСП(X;1). будем рассчитывать с помощью функции Excel НОРМ.СТ.РАСП(X;1).Проверим гипотезу с помощью критерия Пирсона: 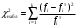 Расчет проведен в таблице (табл. 3). Таблица 3
С помощью функции Excel ХИ2.ОБР.ПХ найдем критическое значение критерия для уровня значимости 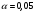 и и 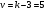 степеней свободы (рис. 4). степеней свободы (рис. 4).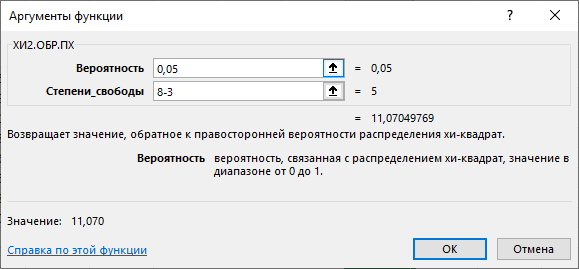 Рис. 4. Определение критического значения для критерия Пирсона Так как фактическое значение больше критического ( | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||