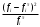Контрольная ПСК 2020. Клочков С.А. МТЗ-301. Контрольная работа по предмету Программные статистические комплексы
 Скачать 403.41 Kb. Скачать 403.41 Kb.
|
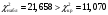 ), нет оснований для принятия нулевой гипотезы. Иными словами, распределение значимо отличается от нормального (рис. 5). ), нет оснований для принятия нулевой гипотезы. Иными словами, распределение значимо отличается от нормального (рис. 5).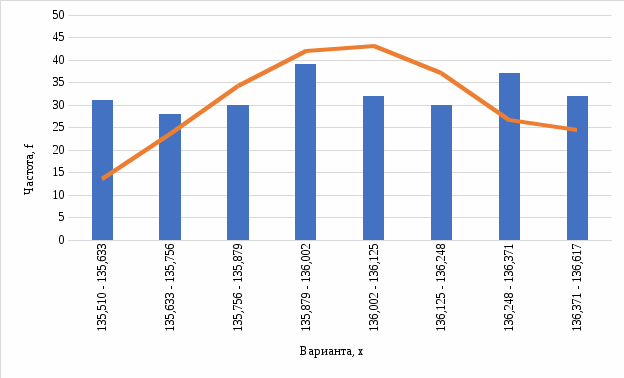 Рис. 5. Диаграмма распределения Выдвинем гипотезу H0: распределение генеральной совокупности X подчинено закону распределения Симпосна с параметрами 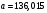 и и 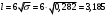 . Проверим эту гипотезу по критерию Пирсона при уровне значимости . Проверим эту гипотезу по критерию Пирсона при уровне значимости 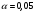 . . Рассчитываем теоретические частоты 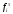 для интервала для интервала 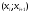 по формуле: по формуле: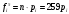 , ,где 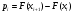 . .Закон «треугольного» распределения Симпсона имеет вид: 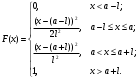 Проверим гипотезу с помощью критерия Пирсона (табл. 4). Таблица 4
С помощью функции Excel ХИ2.ОБР.ПХ найдем критическое значение критерия для уровня значимости 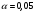 и и 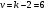 степеней свободы. степеней свободы.Так как фактическое значение больше критического ( 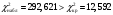 ), нет оснований для принятия нулевой гипотезы. Иными словами, распределение значимо отличается от «треугольного» распределения Симпсона (рис. 6). ), нет оснований для принятия нулевой гипотезы. Иными словами, распределение значимо отличается от «треугольного» распределения Симпсона (рис. 6).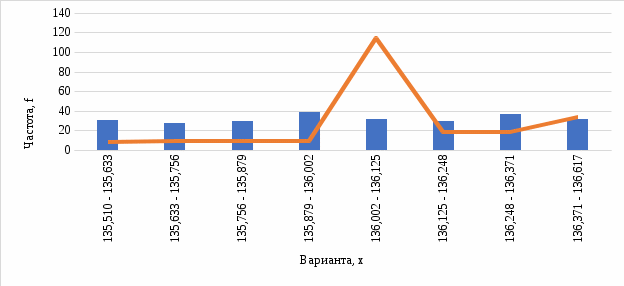 Рис. 6. Диаграмма распределения Выдвинем гипотезу H0: распределение генеральной совокупности X подчинено закону равномерному закону распределения. Проверим эту гипотезу по критерию Пирсона при уровне значимости 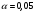 . . Рассчитываем теоретические частоты 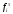 для интервала для интервала 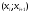 по формуле: по формуле: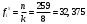 . .Проверим гипотезу с помощью критерия Пирсона (табл. 5). Таблица 5
С помощью функции Excel ХИ2.ОБР.ПХ найдем критическое значение критерия для уровня значимости 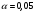 и и 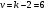 степеней свободы. степеней свободы.Так как фактическое значение меньше критического ( 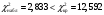 ), нет оснований отвергнуть нулевой гипотезы. Иными словами, распределение близко к равномерному (рис. 7). ), нет оснований отвергнуть нулевой гипотезы. Иными словами, распределение близко к равномерному (рис. 7).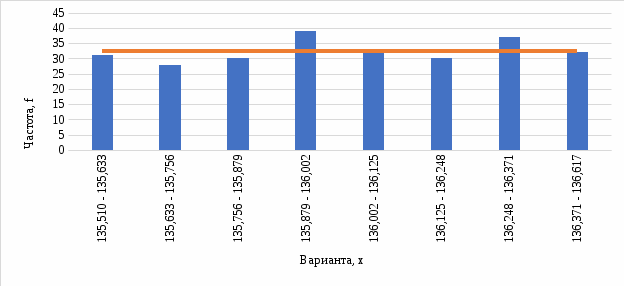 Рис. 6. Диаграмма распределения 5. Границы интервала значений случайной величины, симметричного относительно среднего определяются по формуле: 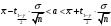 Так как объем данных превышает 30 единиц, параметр 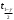 определяем с помощью функции Excel НОРМ.СТ.ОБР. определяем с помощью функции Excel НОРМ.СТ.ОБР.Расчеты проведем в таблице (табл.6). Таблица 6
Для всех интервалов полученные границы попадают в интервал 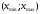 , что также соответствует границам равномерного распределения. , что также соответствует границам равномерного распределения.Определим границы нормального распределения: 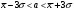 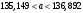 Определим границы распределения Симпсона: 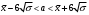 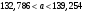 Как видно, все доверительные интервалы среднего также попадают в границы нормального и треугольного распределений. 6. Рассмотрим интервал 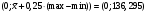 . .Определим количество попадающих в данный интервал с помощью функции Excel СЧЕТЕСЛИ (рис. 7). 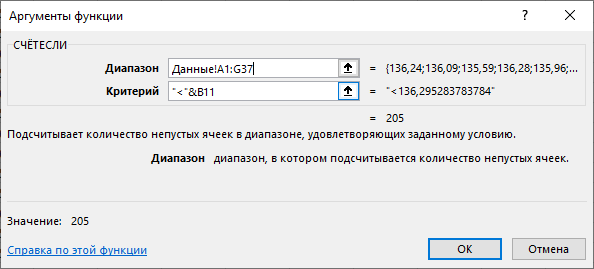 Рис. 7. Определение числа значений Так как в данный интервал попадает 205 значений, следовательно, их доля в общем объеме равна 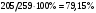 . . |