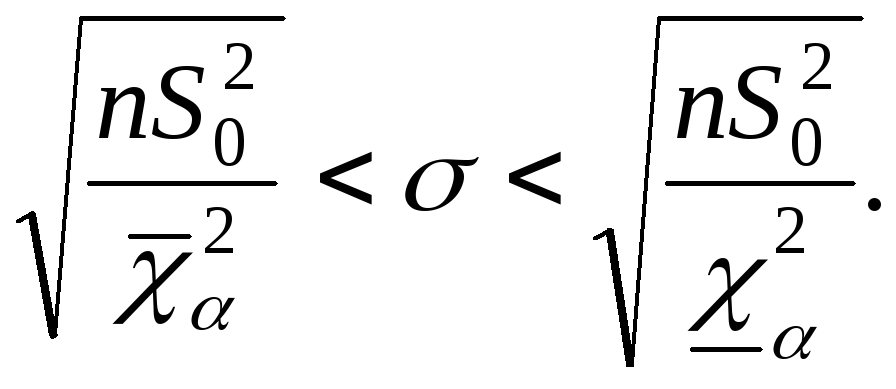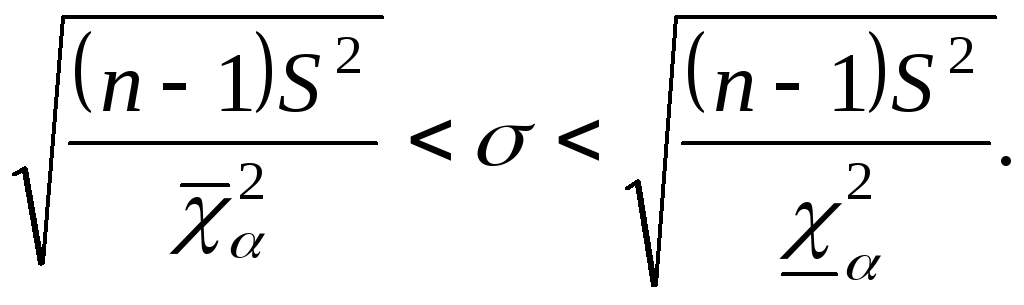29. Интервальные оценки математического ожидания и дисперсии.
Рассматривается выборка 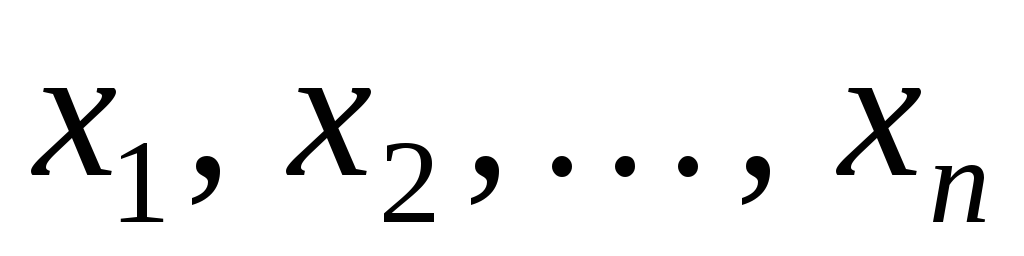 некоторой генеральной случайной величины. Поставим задачу нахождения интервала, покрывающего величину некоторой генеральной случайной величины. Поставим задачу нахождения интервала, покрывающего величину  с заданной вероятностью, близкой к единице. Требуется определить статистики (границы интервала) с заданной вероятностью, близкой к единице. Требуется определить статистики (границы интервала)
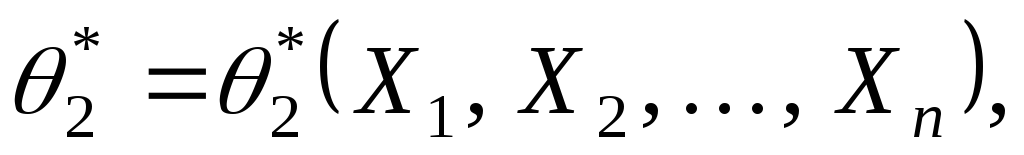
такие, что интервал 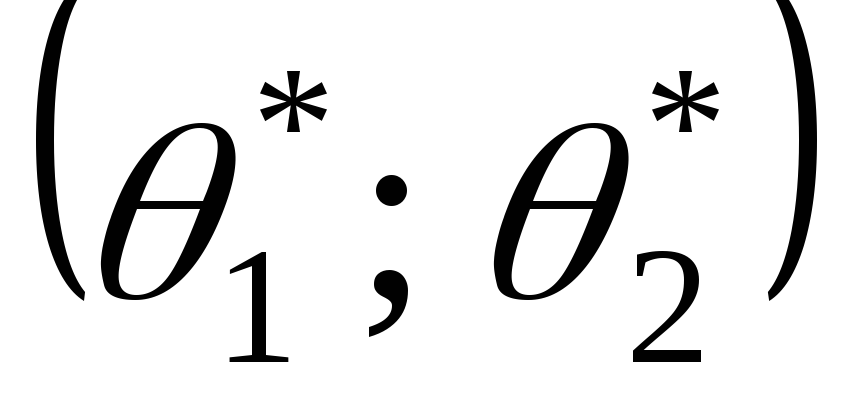 накрывает величину накрывает величину  с вероятностью с вероятностью 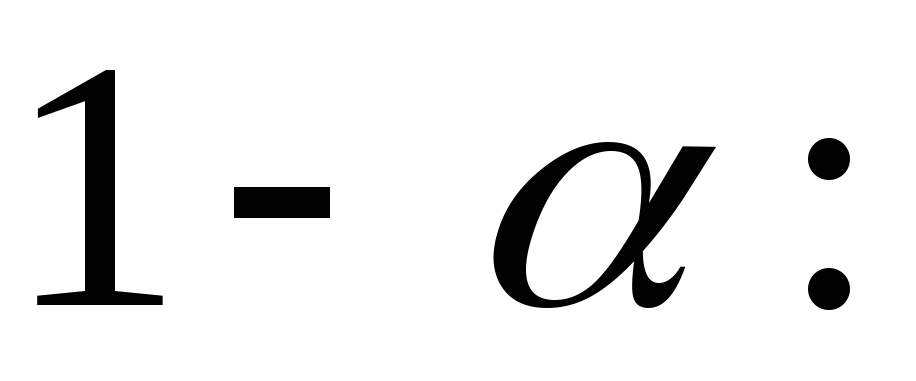
 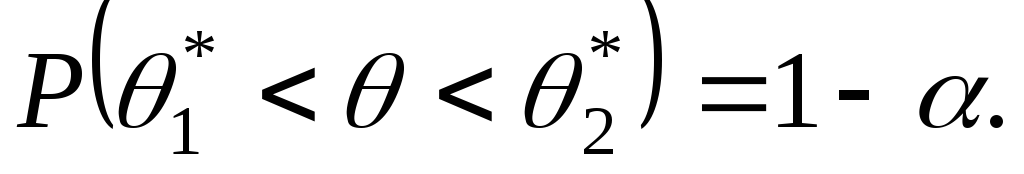
Интервал 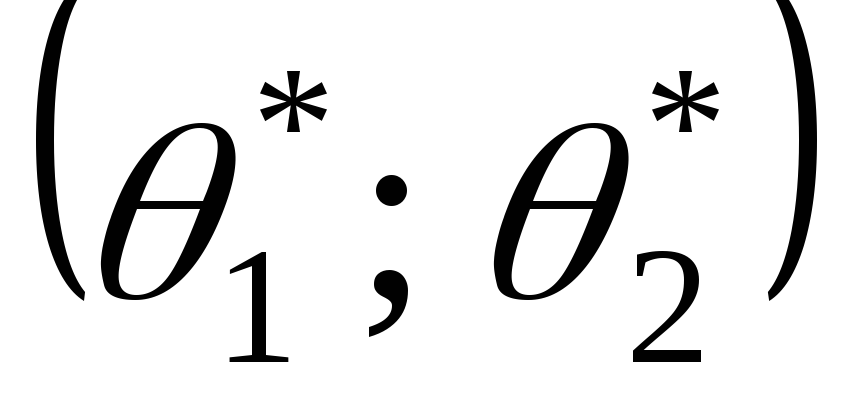 называется интервальной оценкой, или доверительным интервалом. называется интервальной оценкой, или доверительным интервалом.
Интервальные оценки математического ожидания при неизвестной дисперсии
Генеральная случайная величина Х распределена нормально с неизвестным математическим ожиданием и неизвестной дисперсией 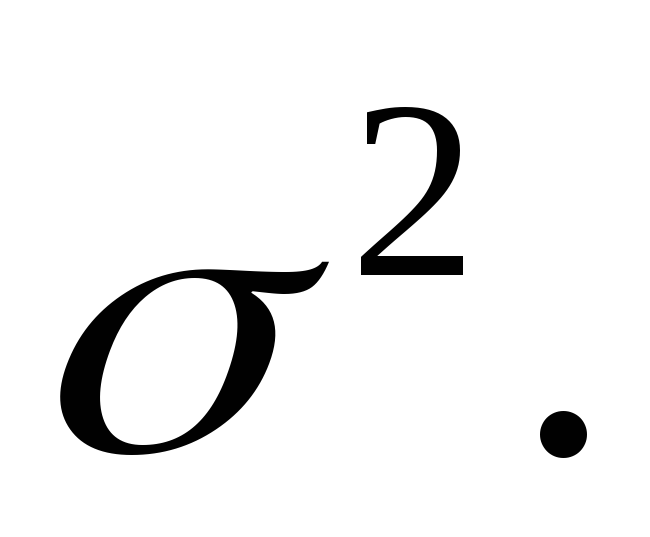 Эффективной оценкой для параметра аявляется оценка Эффективной оценкой для параметра аявляется оценка 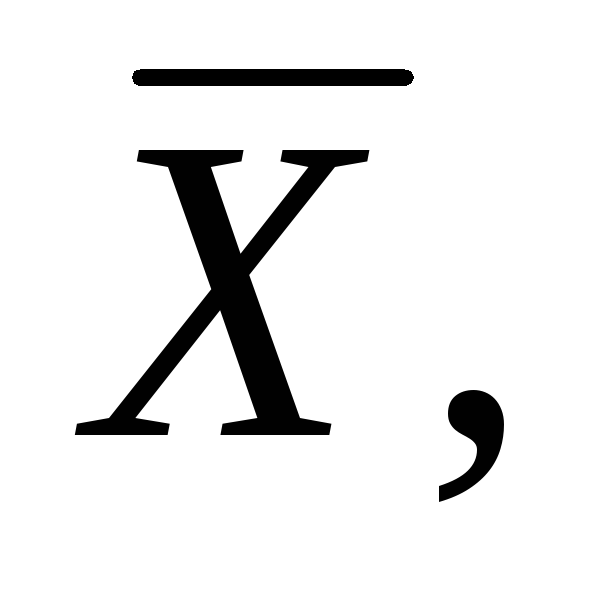 а эффективной оценкой для дисперсии является а эффективной оценкой для дисперсии является 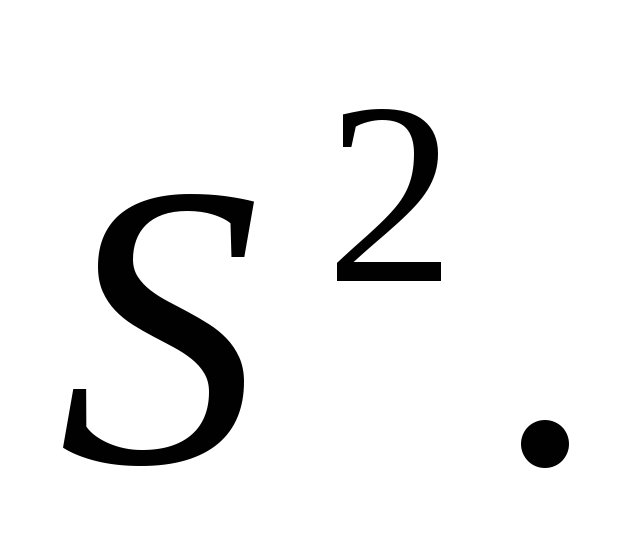 Статистика Статистика 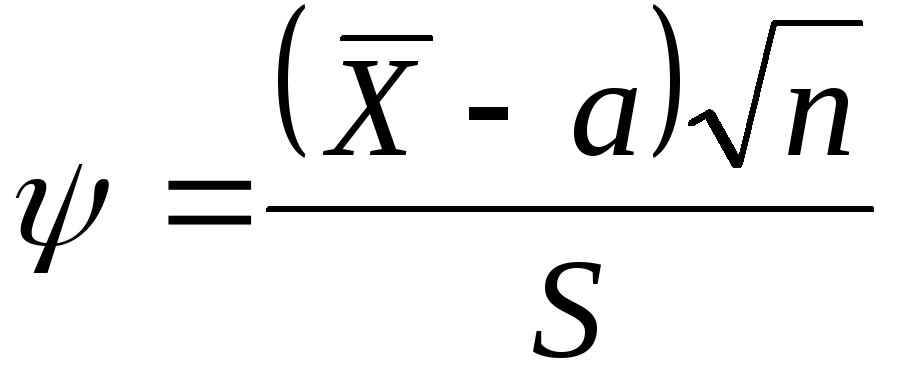 имеет распределение Стьюдента с имеет распределение Стьюдента с 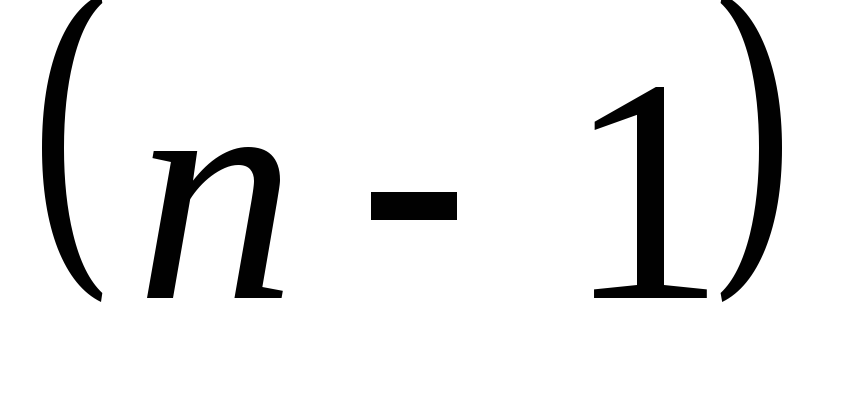 степенью свободы. Распределение этой статистики не зависит от параметроваи степенью свободы. Распределение этой статистики не зависит от параметроваи 
Случайную величину, имеющую распределение Стьюдента с kстепенями свободы, принято обозначать 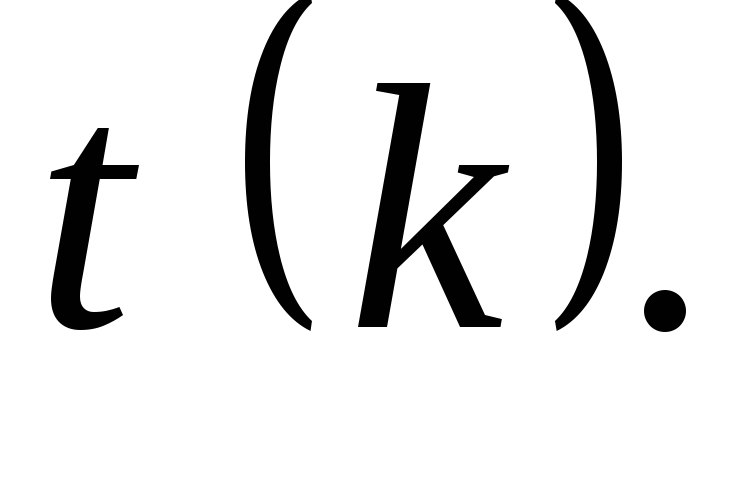 В таблице 2 даны значения В таблице 2 даны значения 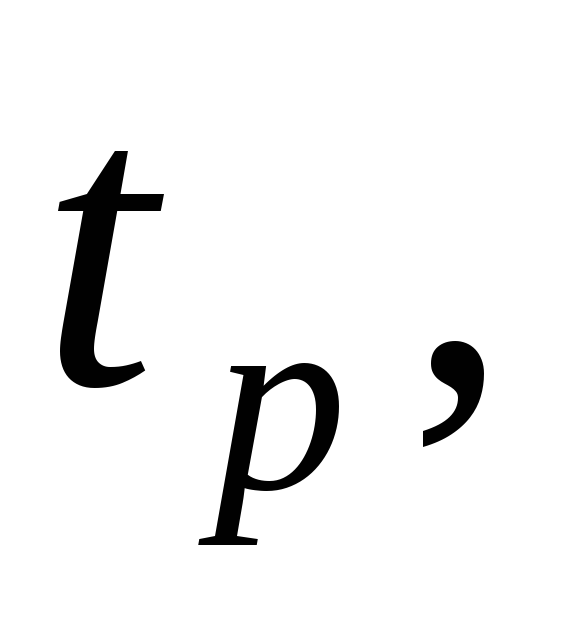 соответствующие вероятности соответствующие вероятности 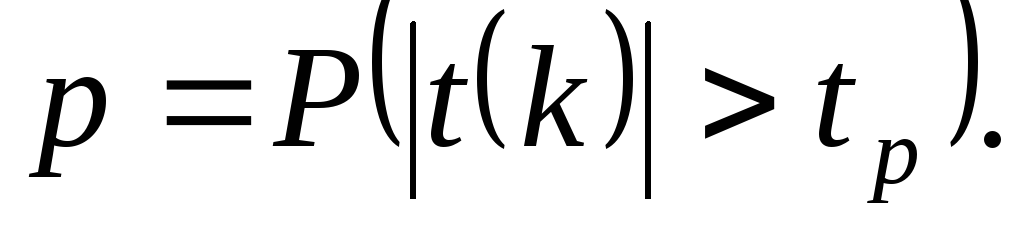 Задавая число степеней свободыkи вероятностьр, находим значение Задавая число степеней свободыkи вероятностьр, находим значение 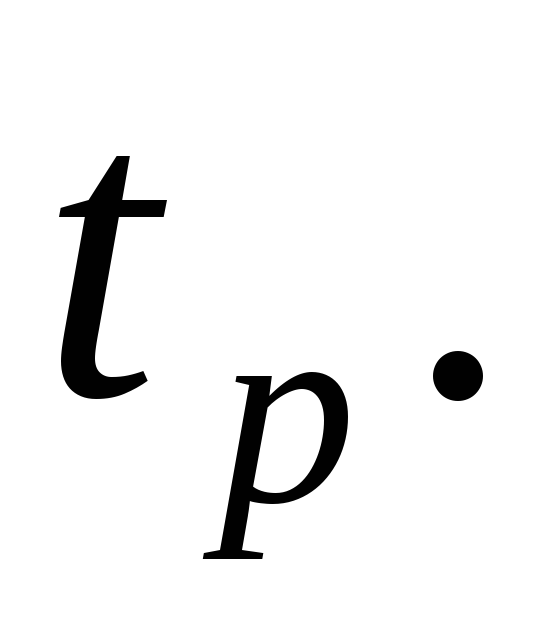 По По 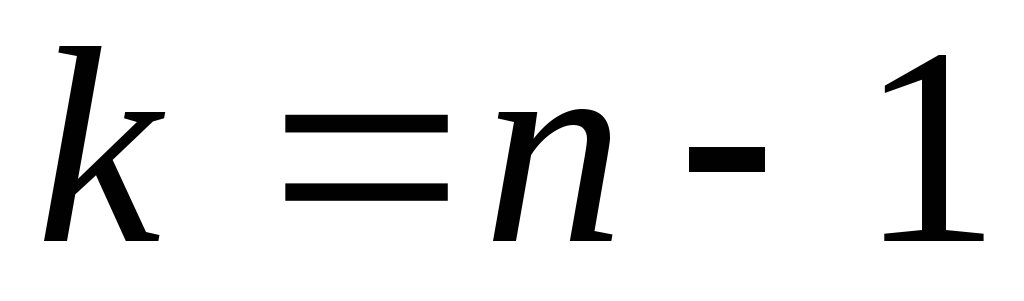 и и 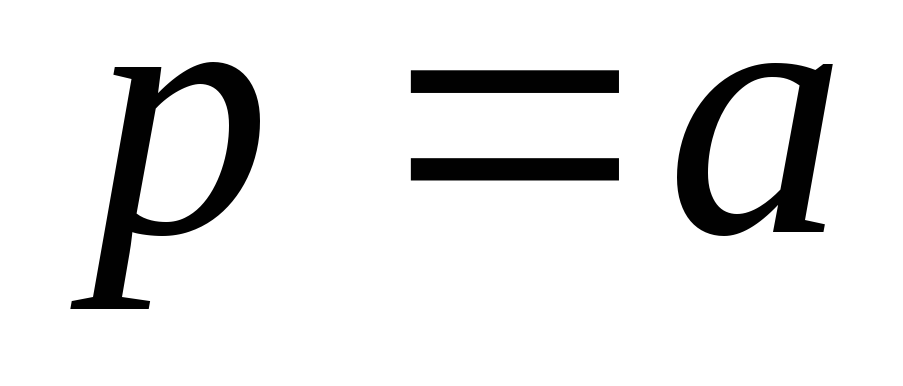 при помощи таблицы 2 определяем значение при помощи таблицы 2 определяем значение 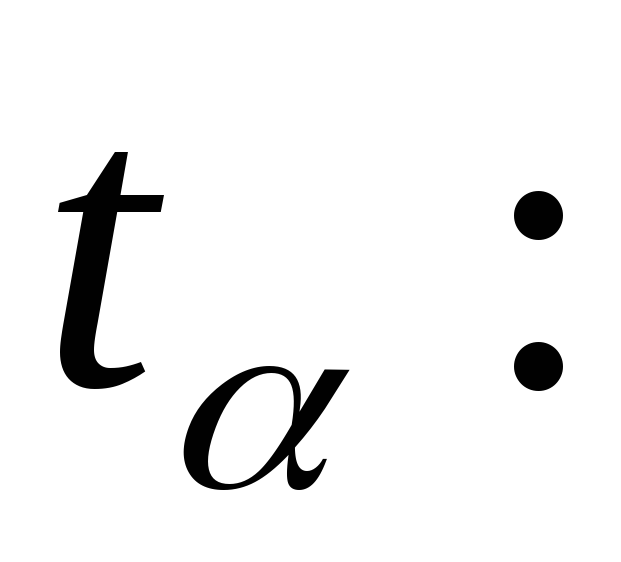
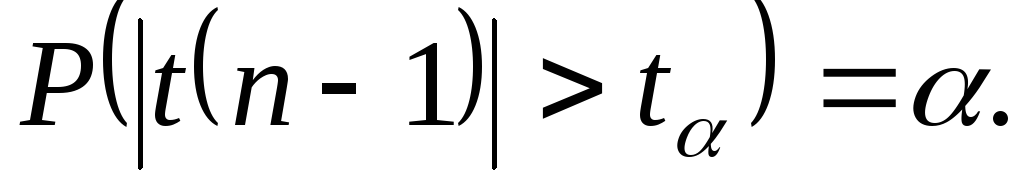
И так как распределение статистики 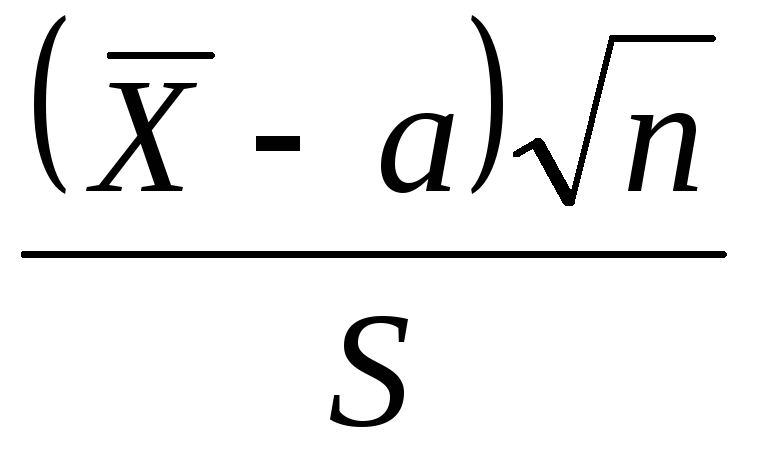 совпадает с распределением совпадает с распределением 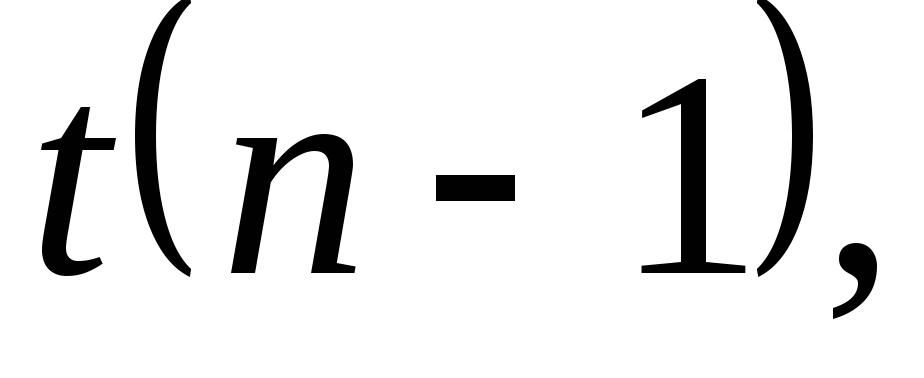 то имеем: то имеем:
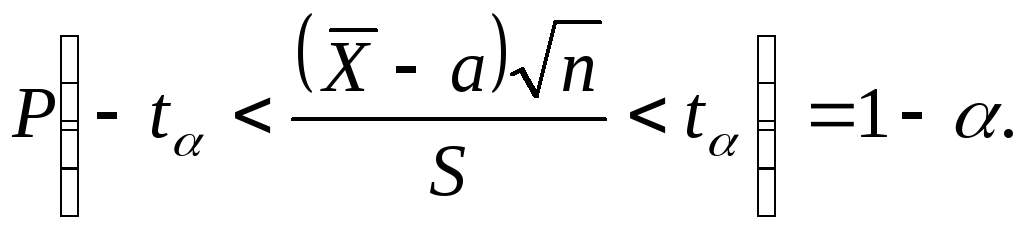
Решаем неравенство 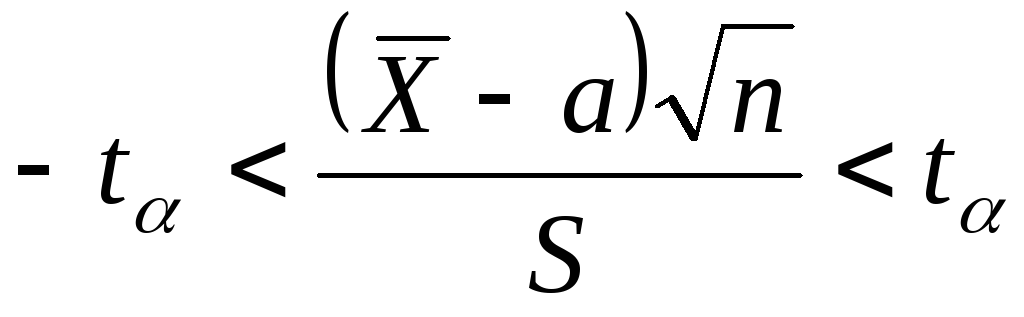 относительноа, получаем: относительноа, получаем:
При этом  ошибка оценки параметрааравна ошибка оценки параметрааравна 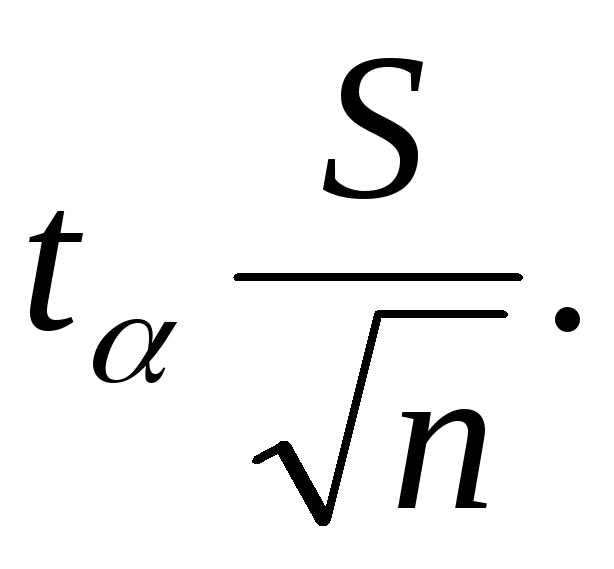 Таким образом,с вероятностью Таким образом,с вероятностью 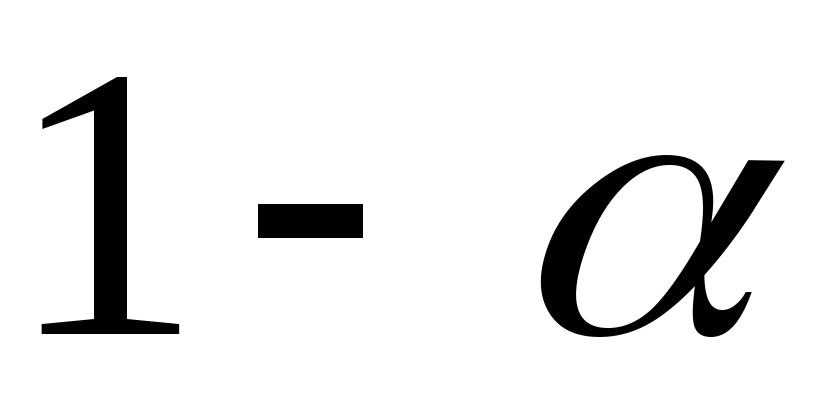 доверительный интервал доверительный интервал 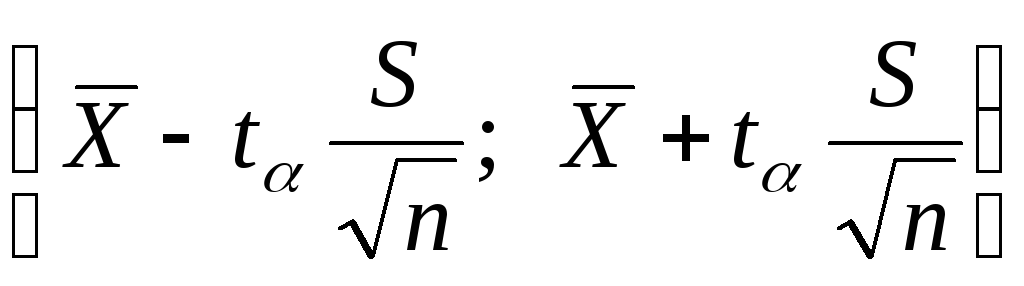 покрывает величинуа. покрывает величинуа.
5.2.3 Интервальные оценки дисперсии (среднеквадратического отклонения) при известном математическом ожидании
Рассматривается случайная выборка 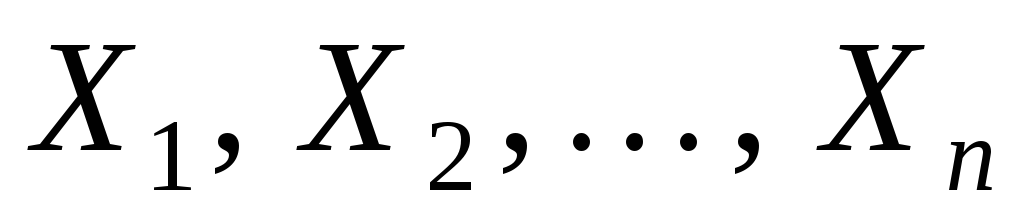 генеральной случайной величиныХ, нормально распределенной с известным математическим ожиданиемаи неизвестной дисперсией генеральной случайной величиныХ, нормально распределенной с известным математическим ожиданиемаи неизвестной дисперсией 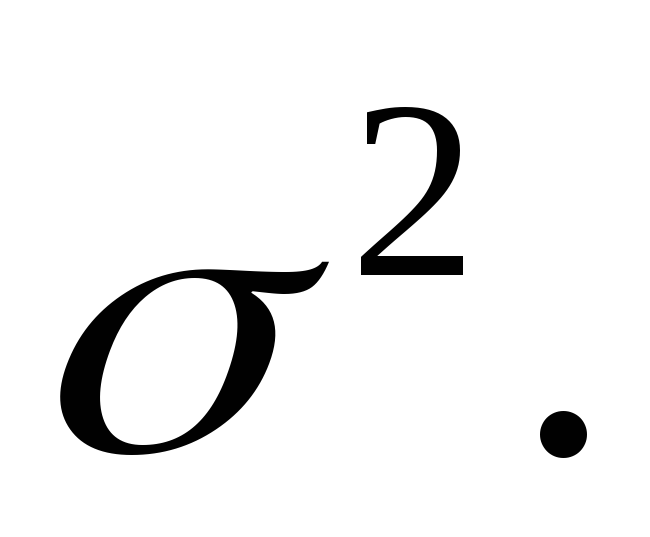 Эффективной оценкой дисперсии является Эффективной оценкой дисперсии является 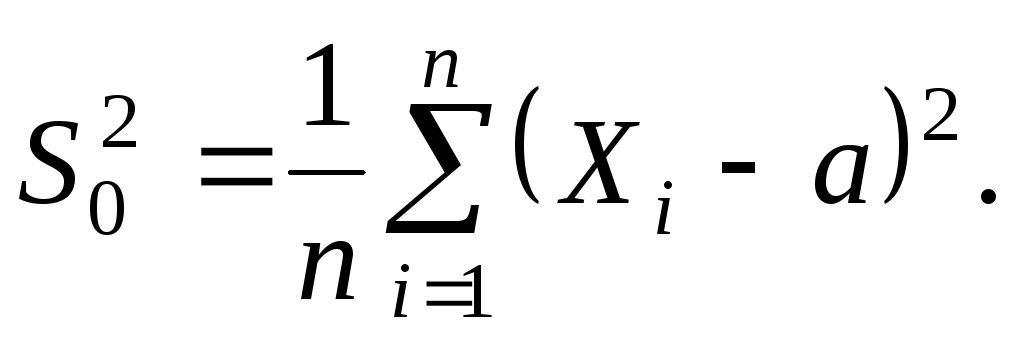 Статистика Статистика 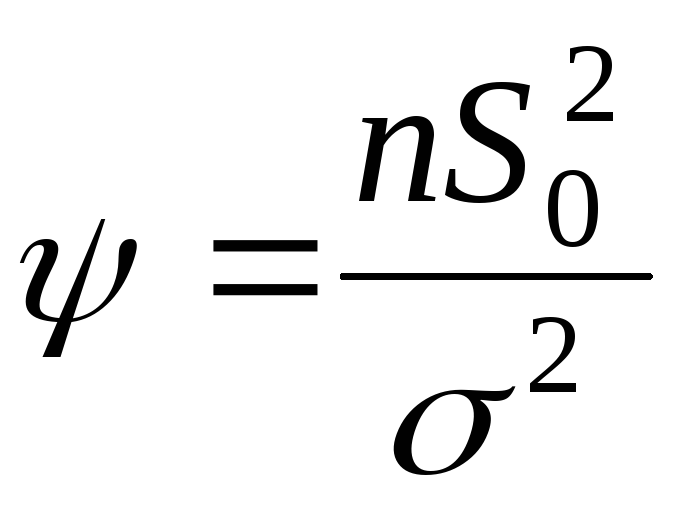 распределена по закону распределена по закону 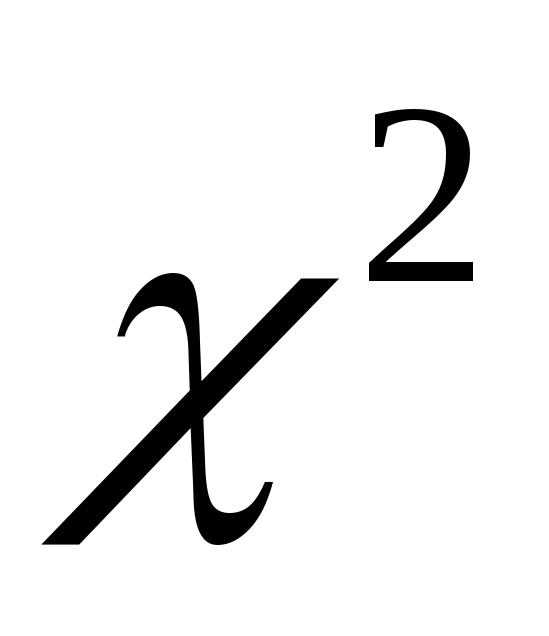 спстепенями свободы. Распределение спстепенями свободы. Распределение  от величины от величины 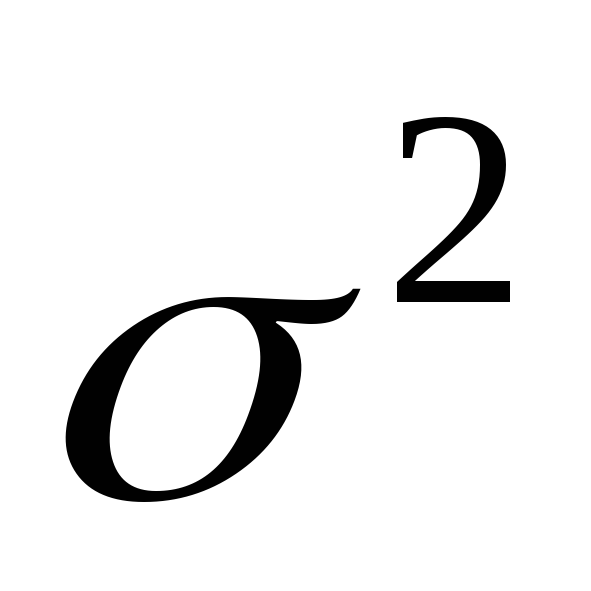 не зависит. не зависит.
Случайную величину, распределенную по закону 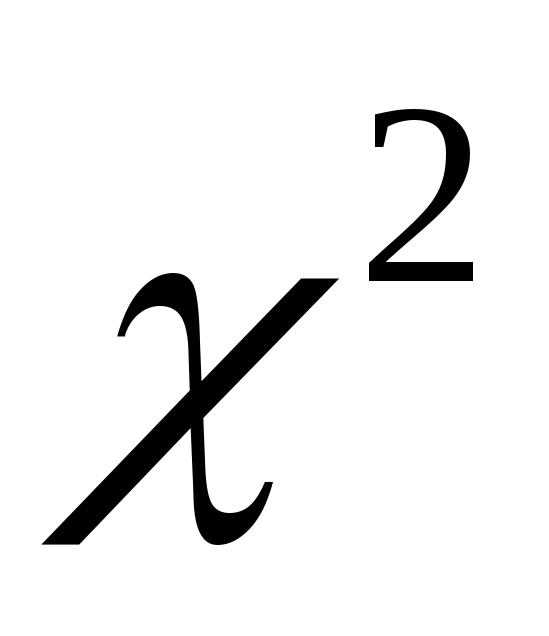 сkстепенями свободы, принято обозначать сkстепенями свободы, принято обозначать 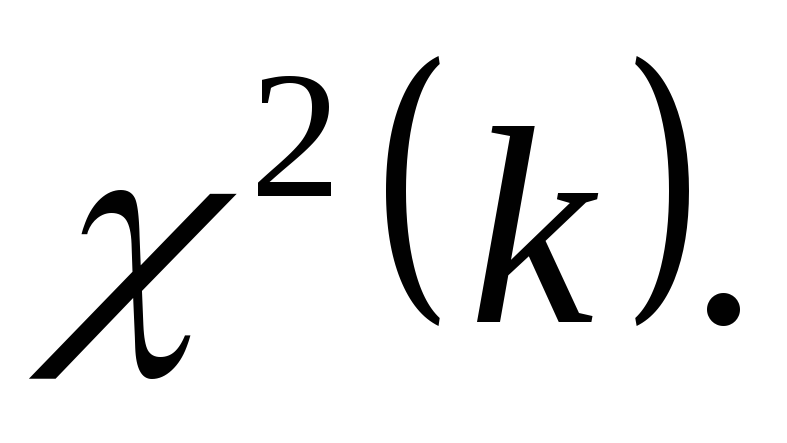 В таблице 3 указаны значения В таблице 3 указаны значения 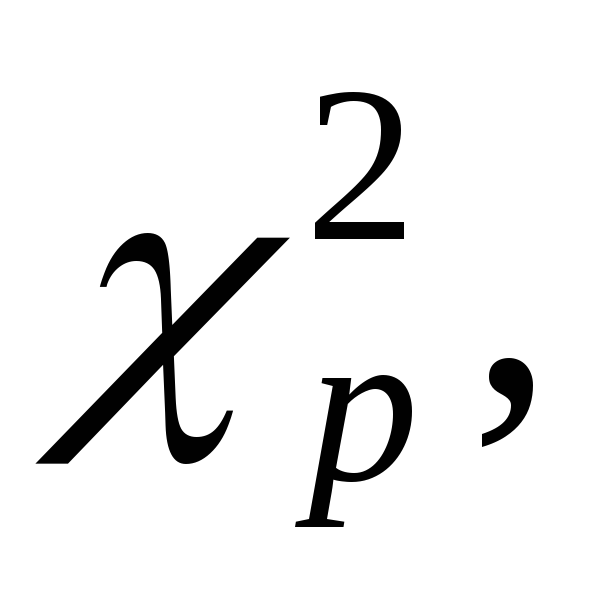 соответствующие вероятности соответствующие вероятности 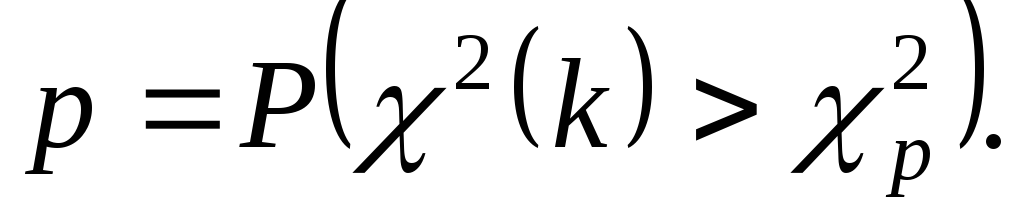 Задаваяри число степеней свободыk, определяем Задаваяри число степеней свободыk, определяем 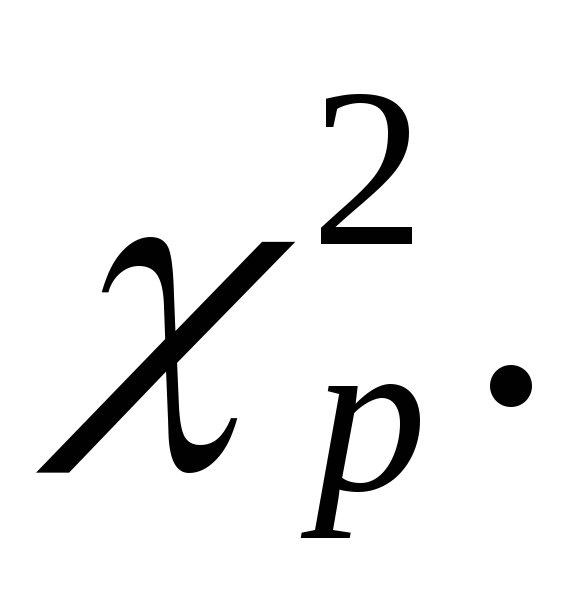 Из таблицы 3 по Из таблицы 3 по 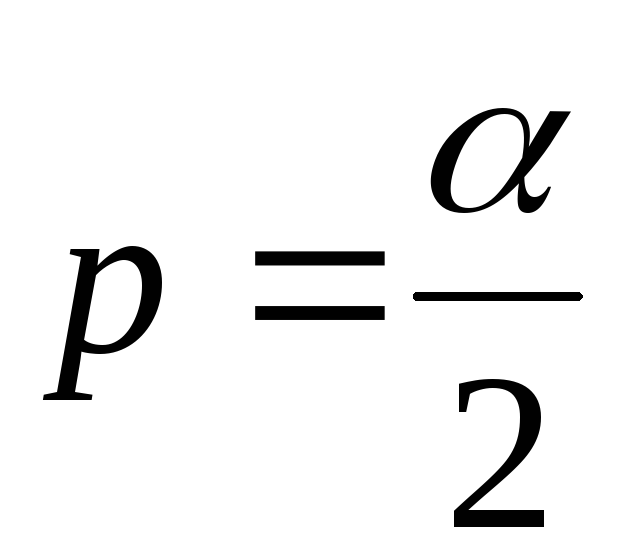 и и 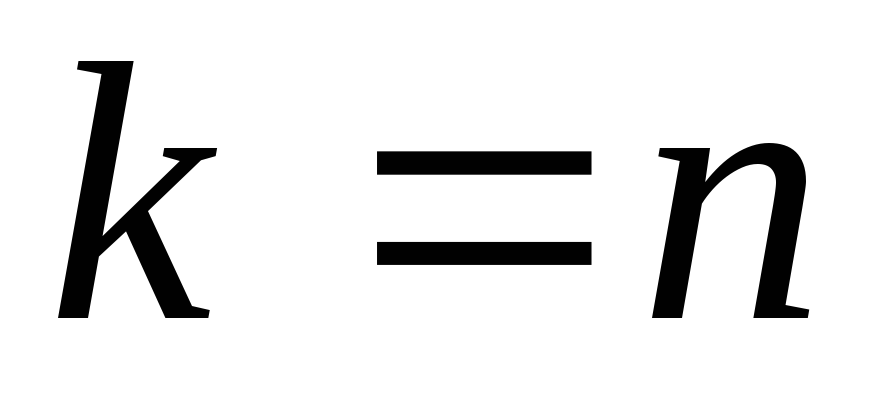 находим находим 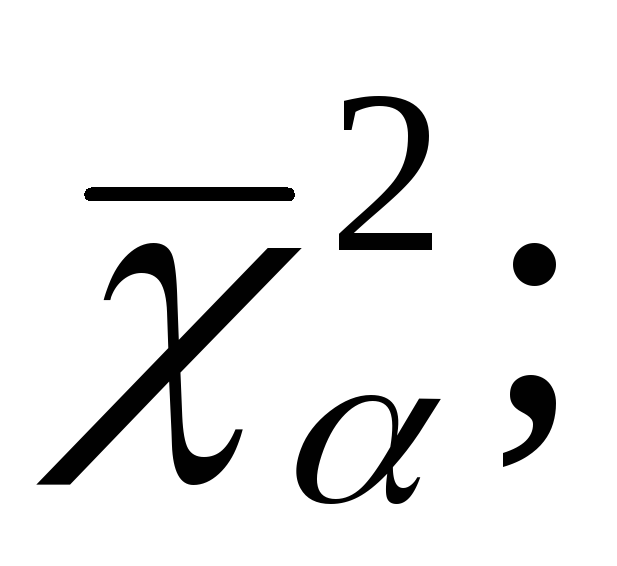 по по 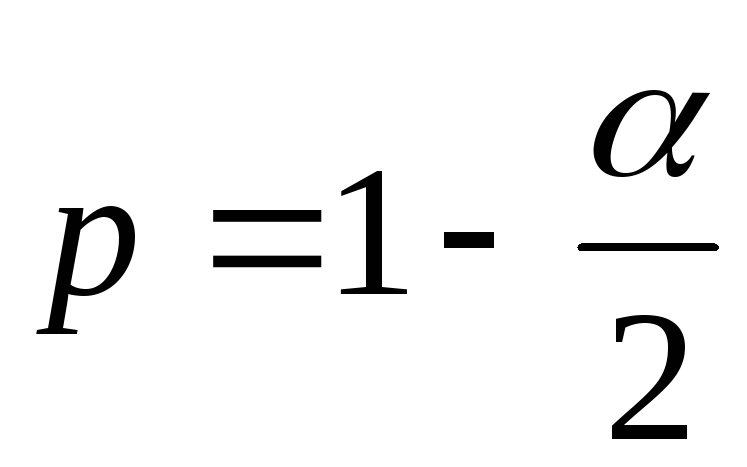 и и 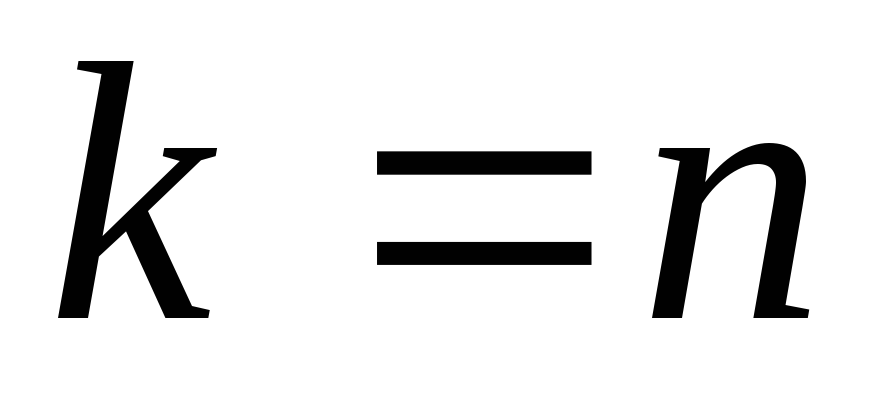 находим находим 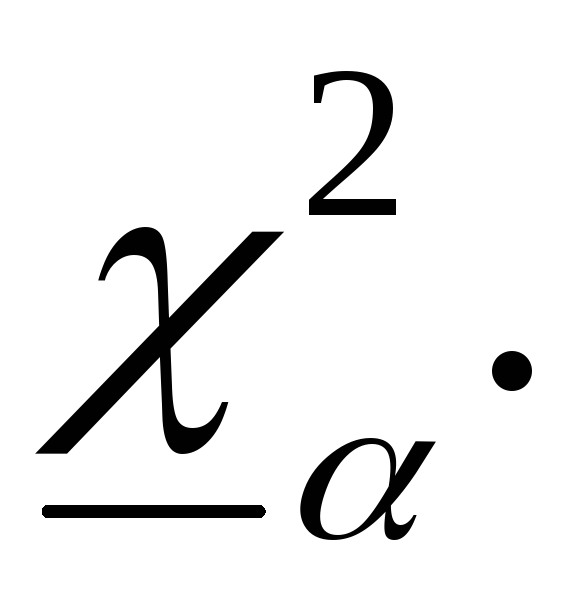 Так как статистика Так как статистика 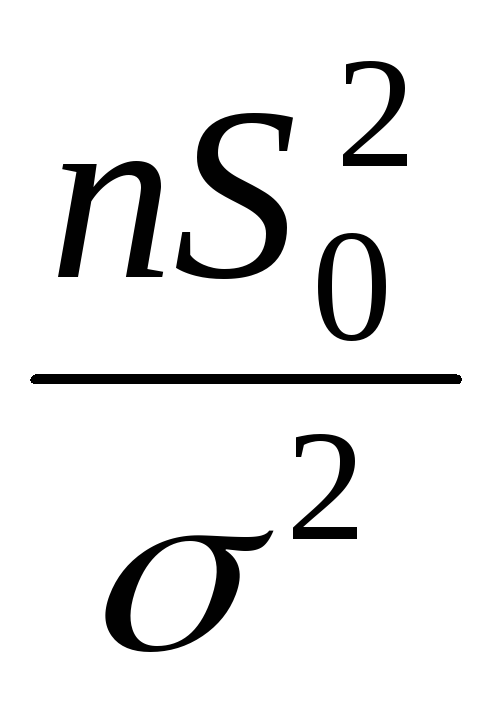 распределена по закону распределена по закону 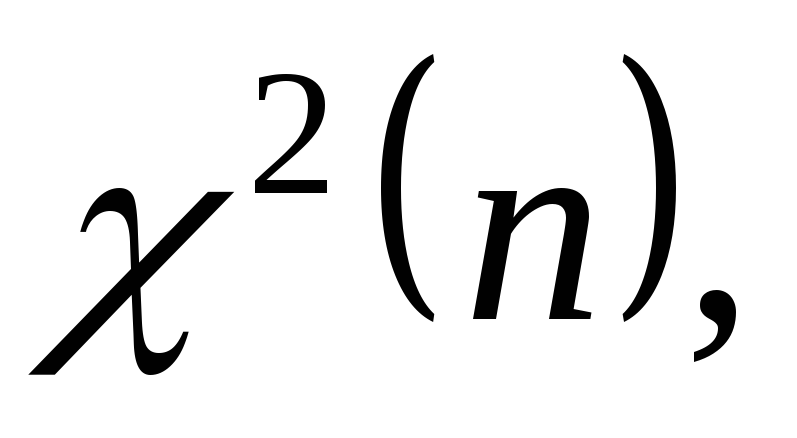 то то
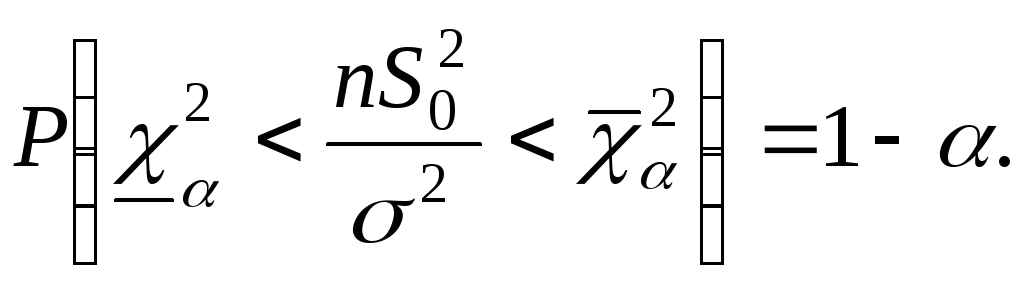
Решаем неравенство 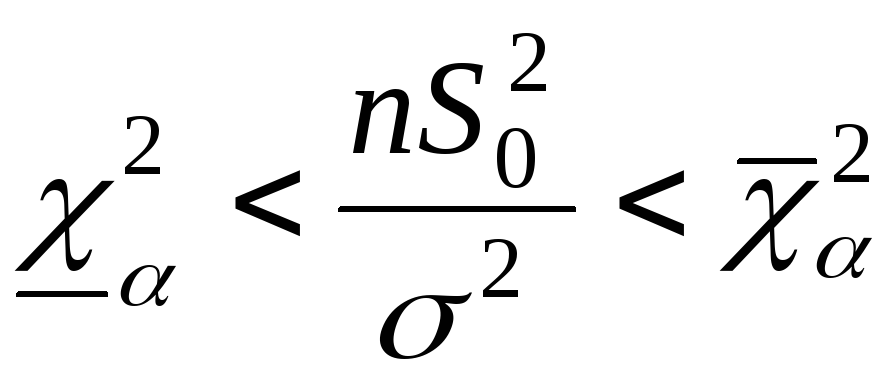 относительно относительно  получаем: получаем:
Итак, с доверительной вероятностью 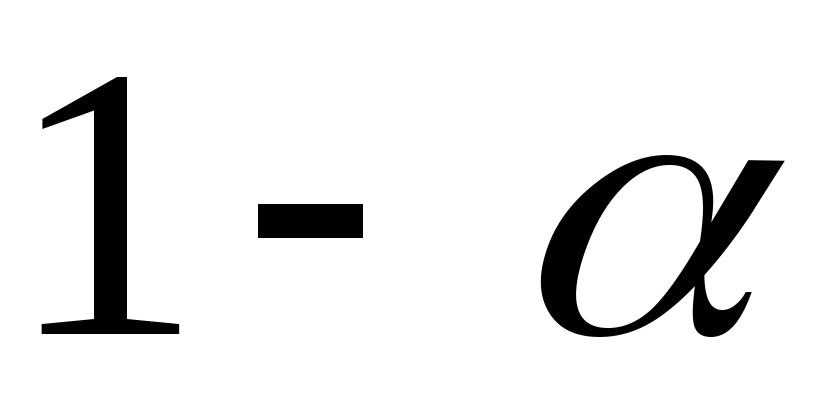 доверительный интервал доверительный интервал 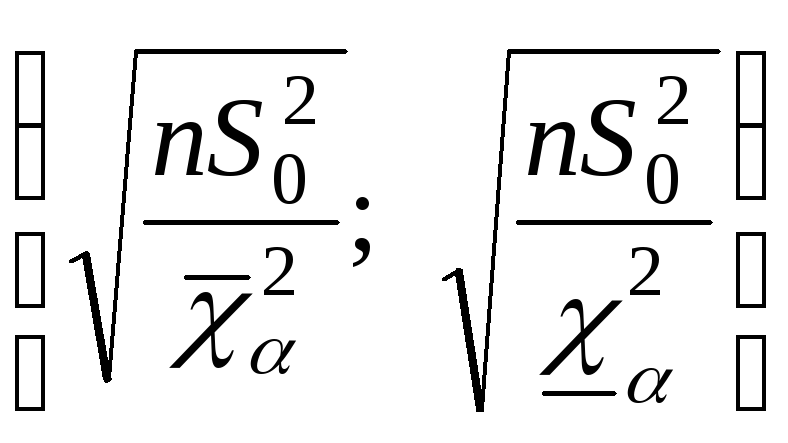 покрывает величину покрывает величину 
В данном случае доверительный интервал не симметричен относительно оценки 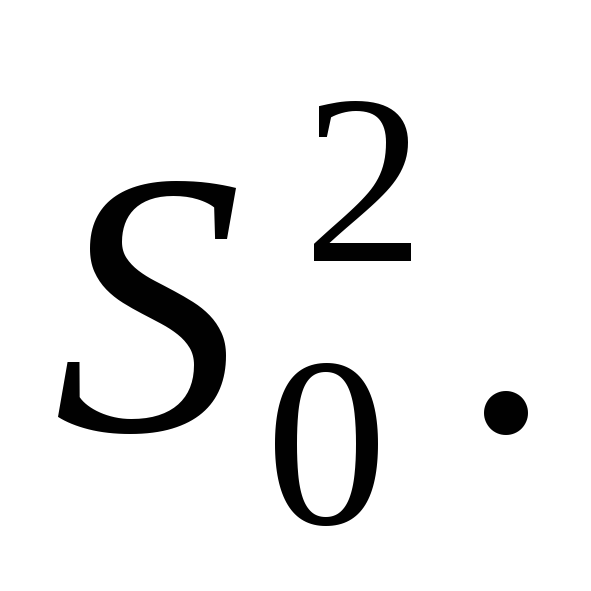
Интервальные оценки дисперсии (среднеквдратического отклонения) при неизвестном математическом ожидании
Рассматривается случайная выборка 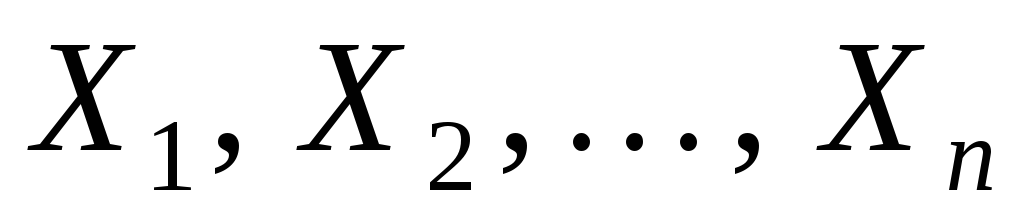 генеральной случайной величиныХ, нормально распределенной с неизвестными параметрамиаи генеральной случайной величиныХ, нормально распределенной с неизвестными параметрамиаи  Наилучшей оценкой дисперсии является Наилучшей оценкой дисперсии является 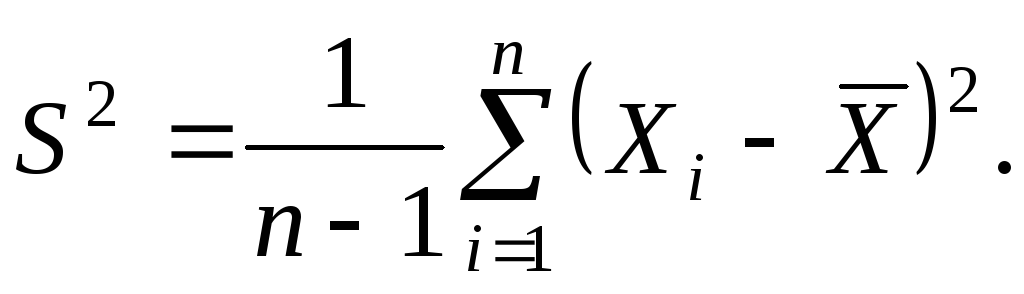 Распределение статистики Распределение статистики 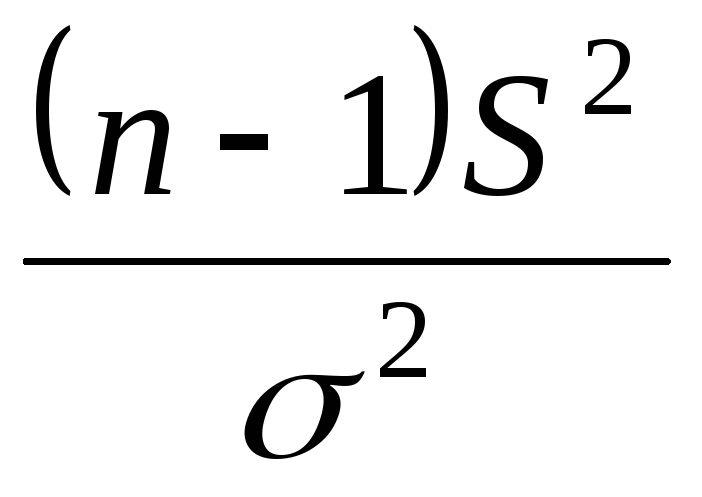 совпадает с распределением совпадает с распределением 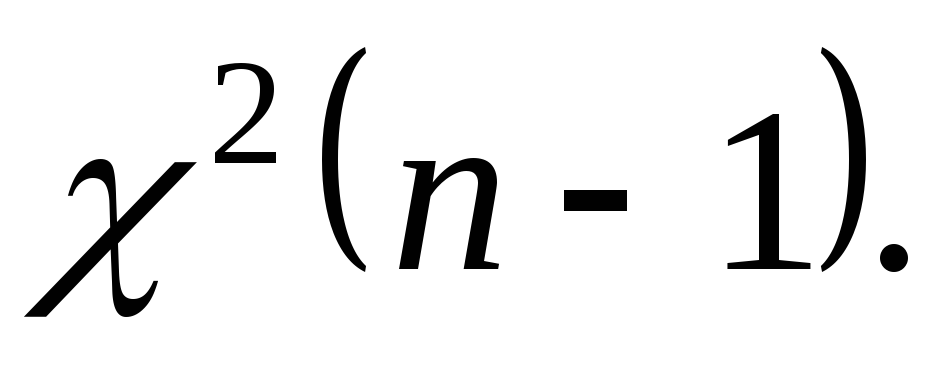 Используем таблицу 3: по Используем таблицу 3: по 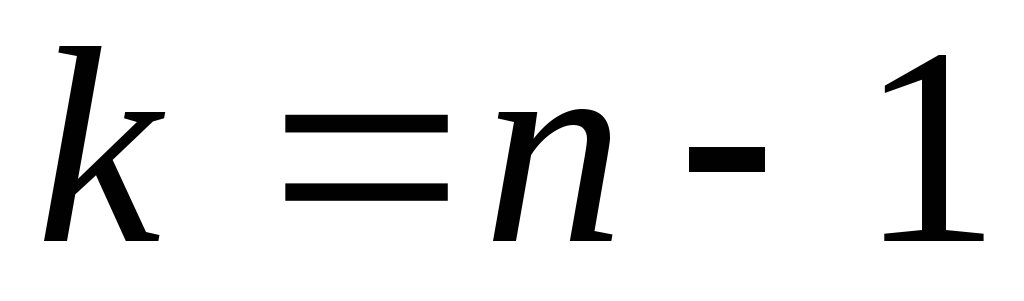 и и 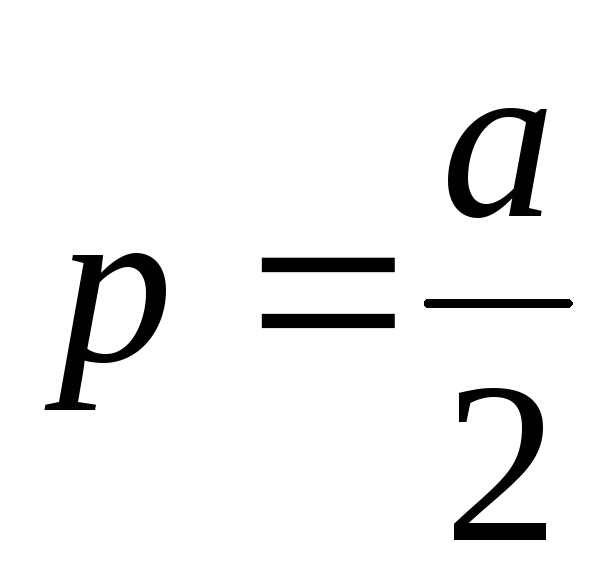 находим находим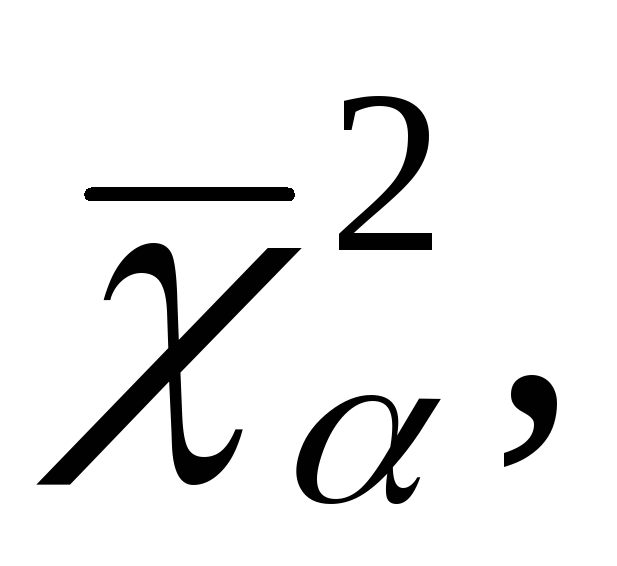 по по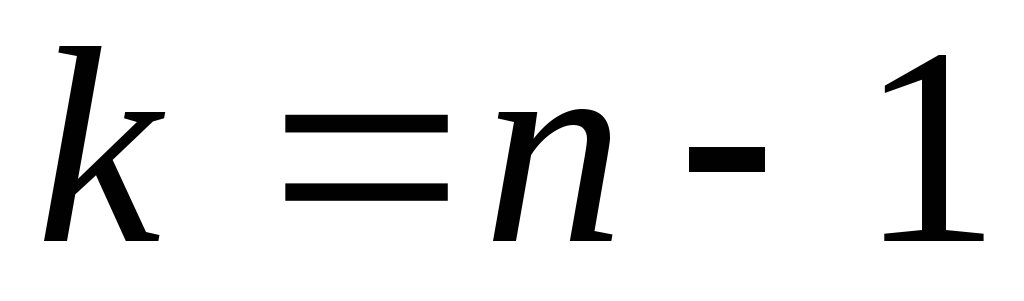 и и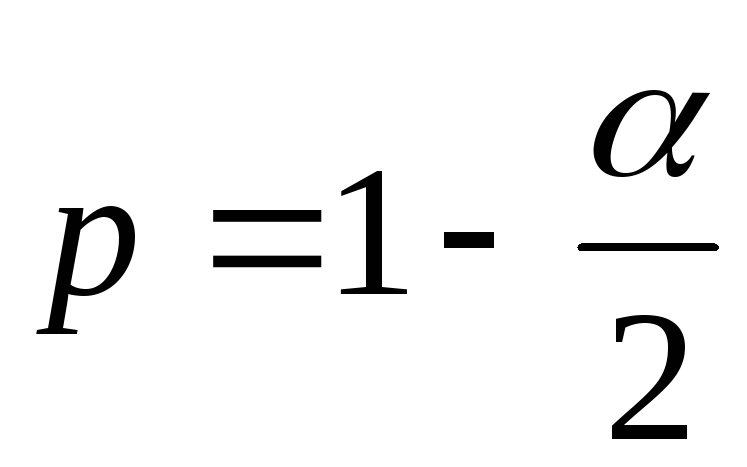 находим находим 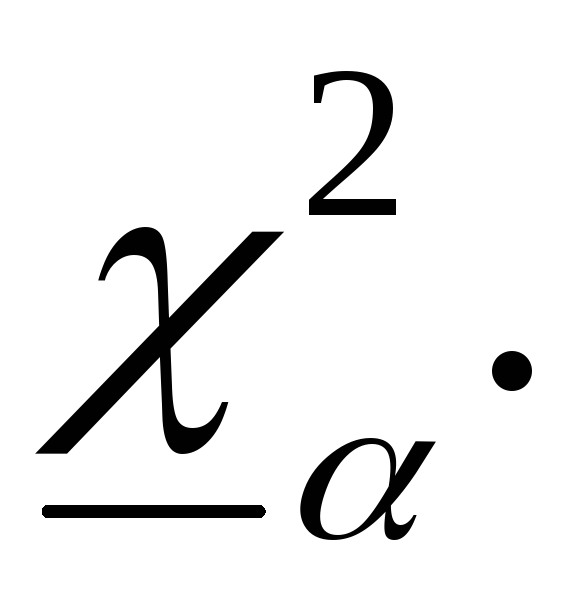 С вероятностью С вероятностью 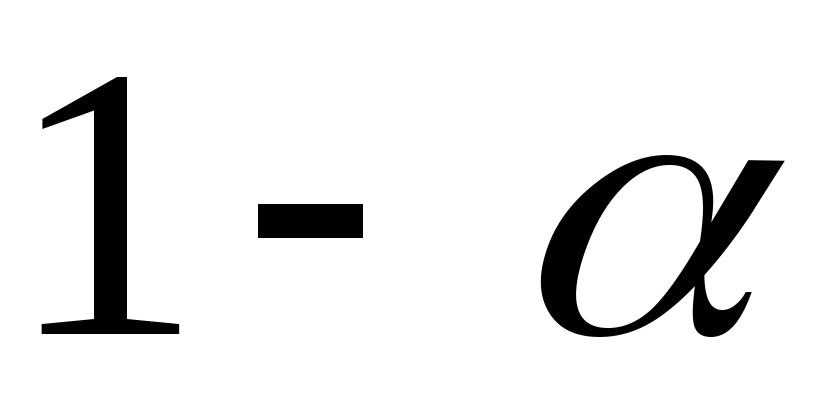 выполняется неравенство: выполняется неравенство:
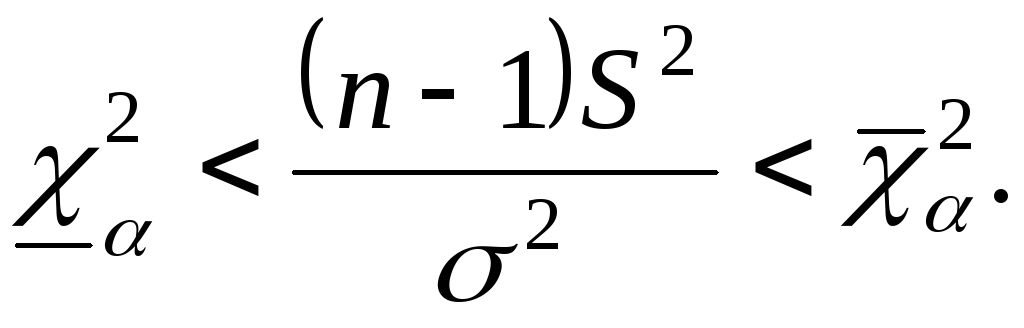
Разрешим это неравенство относительно 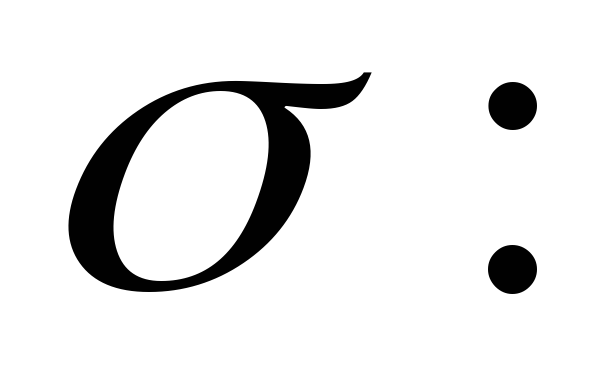
С доверительной вероятностью 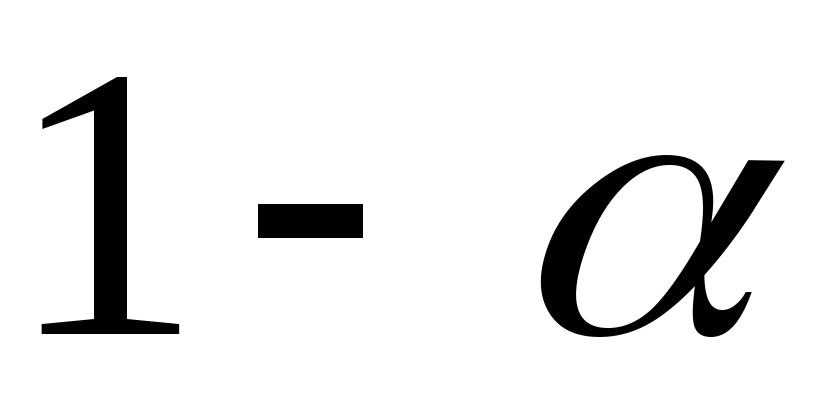 доверительный интервал доверительный интервал 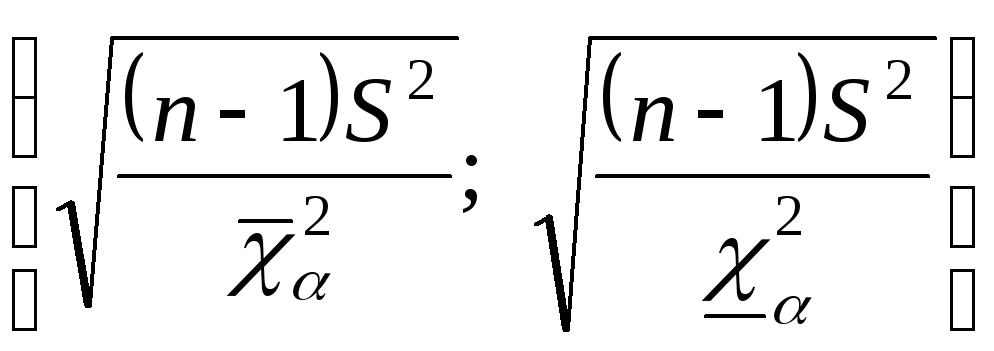 покрывает параметр покрывает параметр  |
 Скачать 1.12 Mb.
Скачать 1.12 Mb.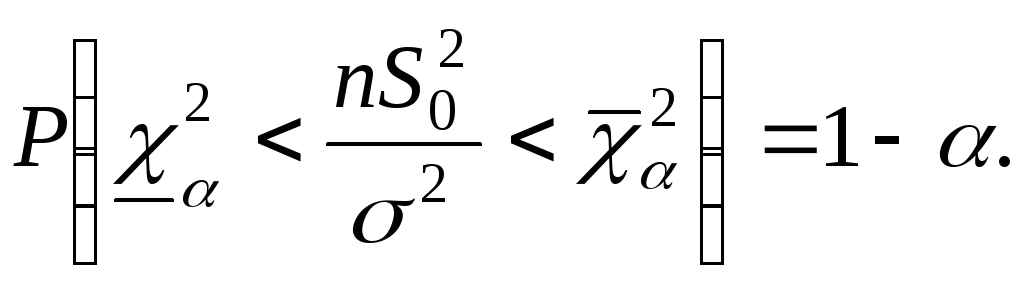
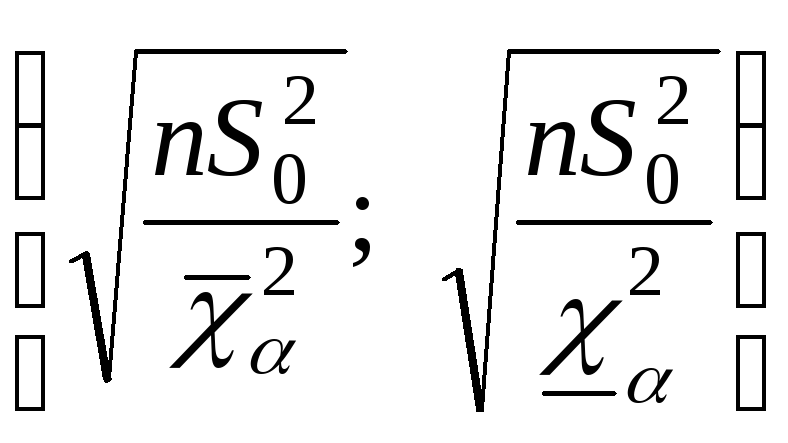 покрывает величину
покрывает величину 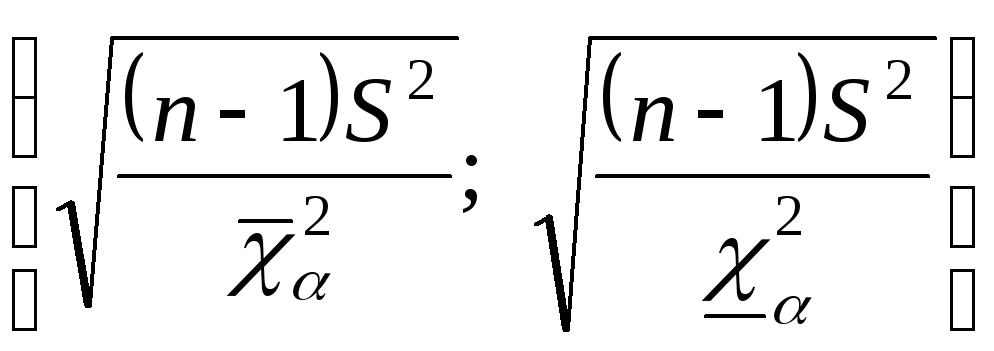 покрывает параметр
покрывает параметр