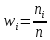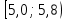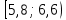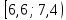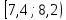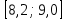Контрольная работа по статистике 13. 03. 02. код направления подготовки
 Скачать 72.14 Kb. Скачать 72.14 Kb.
|
|
Министерство науки и высшего образования РФ федеральное государственное бюджетное образовательное учреждение высшего образования «Вологодский государственный университет» Институт машиностроения, энергетики и транспорта (наименование института) Кафедра электрооборудования (наименование кафедры) Дисциплина: «Прикладная математика в энергетике» Наименование темы: «Контрольная работа по статистике»
Вологда 2022 г. 5 КОНТРОЛЬНАЯ РАБОТА Задача Суточное потребление электроэнергии на рабочем месте в цехе может быть рассмотрено как случайная величина Х, распределенная по нормальному закону. Было произведено 40 измерений этой величины (табл. 5.1). 1.1 Провести группировку данных, разбив варианты на 5 интервалов. 1.2 Для сгруппированного ряда построить гистограмму частот. 2.1 Найти выборочную среднюю, выборочную дисперсию, исправленную выборочную дисперсию, исправленное выборочное среднеквадратическое отклонение случайной величины Х. 2.2 Построить доверительный интервал для генеральной средней и генерального среднеквадратического отклонения с заданным уровнем доверительной вероятности γ = 0,95. 3.1 При уровне значимости α = 0,05 проверить утверждение энергослужб предприятия, что среднесуточное потребление электроэнергии на рабочем месте равно a (табл. 5.2). 3.2 После переналадки оборудования, произведенной с целью уменьшения потребления электроэнергии, были проведены новые измерения, и получена выборка объема 10 (табл. 5.3.). При уровне значимости α проверить, является ли статистически обоснованным утверждение производителя об уменьшении среднего потребления электроэнергии. Таблица 5.1
Таблица 5.2
Таблица 5.3
Решение Проведем группировку исходных данных, т.е. разобьем варианты на отдельные интервалы. Найдем разность между наибольшим и наименьшим значениями признака: xmax – xmin = 9,05 – 5,06 = 3,99. Тогда при разбивке на 5 интервалов длина интервала составит h = 3,99/5 = 0,798 ≈ 0,8. Для упрощения дальнейших расчетов выберем границы интервалов таким образом, чтобы середины интервалов являлись как можно более «круглыми» числами (с наименьшим числом знаков после запятой). Получим табл. 5.4. Таблица 5.4
1.2 Построим для сгруппированного ряда гистограмму частот. 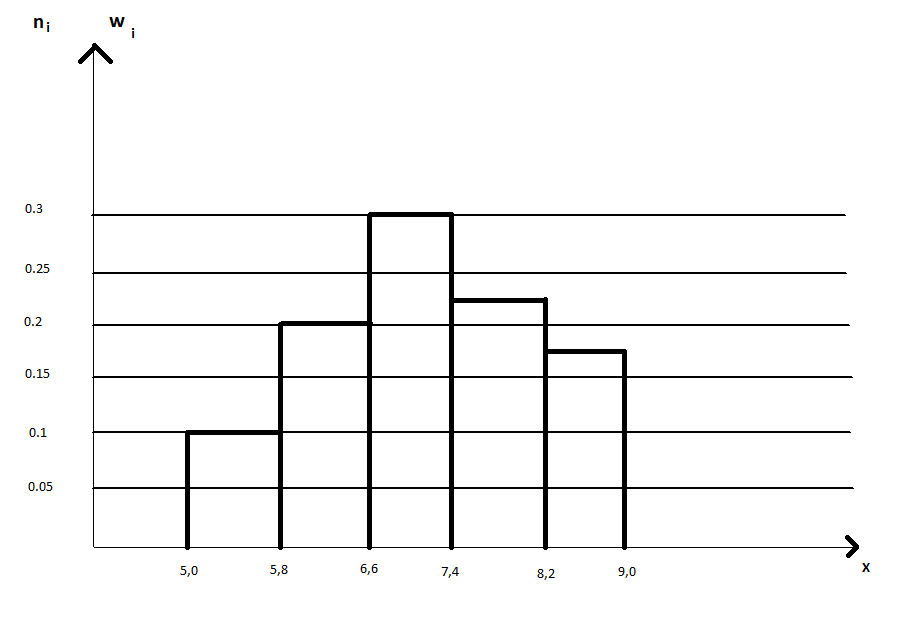 Рис. 1. 2.1 Найдем выборочную среднюю 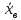 : :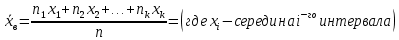 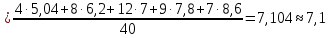 Найдем выборочную дисперсию Dв 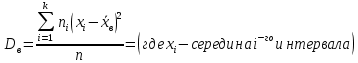 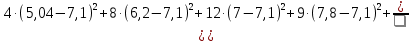 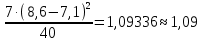 Найдем исправленную выборочную дисперсию: 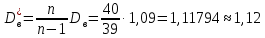 Найдем исправленное выборочное среднеквадратическое отклонение случайной величины Х 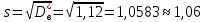 2.2 Построим доверительный интервал для генеральной средней с уровнем доверительной вероятности γ = 0,95. Так как значение генеральной дисперсии неизвестно, воспользуемся формулой 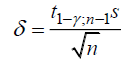 . Найдем значение t1–γ, n–1 = t0,05;39 по таблице критических точек распределения Стьюдента при уровне вероятности α = 0,05 и числе степеней свободы k = n – 1 = 39. Получаем t0,05;39 = 2,02. Далее находим точность оценки . Найдем значение t1–γ, n–1 = t0,05;39 по таблице критических точек распределения Стьюдента при уровне вероятности α = 0,05 и числе степеней свободы k = n – 1 = 39. Получаем t0,05;39 = 2,02. Далее находим точность оценки 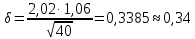 Доверительный интервал для генеральной средней имеет вид x ∈ (6,76; 7,44) Построим доверительный интервал для генерального среднеквадратического отклонения с заданным уровнем доверительной вероятности γ = 0,95. Найдем значение 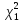 по таблице критических точек распределения χ2 при уровне вероятности (1 + γ) / 2 = 0,975 и числе степеней свободы k = n – 1 = 39. Получаем по таблице критических точек распределения χ2 при уровне вероятности (1 + γ) / 2 = 0,975 и числе степеней свободы k = n – 1 = 39. Получаем 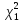 = 22,9, следовательно, χ1 = 4,8. Найдем значение = 22,9, следовательно, χ1 = 4,8. Найдем значение 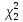 по таблице критических точек распределения χ2 при уровне вероятности (1 – γ) / 2 = 0,025 и числе степеней свободы k = n – 1 = 39. Получаем по таблице критических точек распределения χ2 при уровне вероятности (1 – γ) / 2 = 0,025 и числе степеней свободы k = n – 1 = 39. Получаем 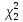 = 58,1, следовательно, χ2 = 7,6. Доверительный интервал для генерального среднеквадратического отклонения имеет вид = 58,1, следовательно, χ2 = 7,6. Доверительный интервал для генерального среднеквадратического отклонения имеет вид 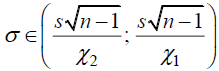 . Подставляя значения, получаем, что с вероятностью 0,95 выполнено . Подставляя значения, получаем, что с вероятностью 0,95 выполнено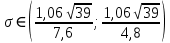 или или 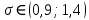 3.1 При уровне значимости α = 0,05 проверим утверждение, что среднее значение величины Х соответствует проектному значению a = 7. Так как выборка имеет большой объем (n = 40 > 30), то для проверки нулевой гипотезы Н0: 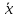 a в качестве критерия проверки можно принять случайную величину U. При этом в качестве генерального среднеквадратического отклонения σ можно принять выборочное значение s. a в качестве критерия проверки можно принять случайную величину U. При этом в качестве генерального среднеквадратического отклонения σ можно принять выборочное значение s.Вычислим наблюдаемое значение критерия 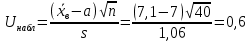 Конкурирующей является гипотеза Н1: x a , поэтому критическую точку Uкр находим по таблице функции Лапласа из условия Φ(Uкр) = (1 – α)/2 = 0,475. Получаем Uкр=1,96. Так как |Uнабл| < Uкр, то нет оснований отвергнуть нулевую гипотезу. Следовательно, утверждение, что среднее значение входного параметра Х соответствует проектному значению, является статистически обоснованным. 3.2 Для первой выборки объема n1 = 40 были получены значения 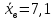 ; s1 = 1,06. Найдем выборочную среднюю и выборочное среднеквадратическое отклонение для второй выборки объема n2 = 10 (табл. 5.3). ; s1 = 1,06. Найдем выборочную среднюю и выборочное среднеквадратическое отклонение для второй выборки объема n2 = 10 (табл. 5.3).Найдем выборочную среднюю: 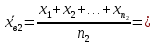 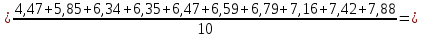 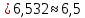 Найдем выборочную дисперсию: 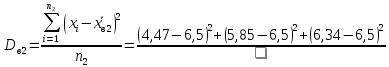 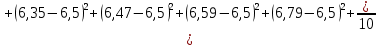 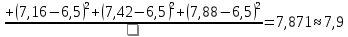 Найдем исправленную выборочную дисперсию по формуле 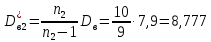 Найдем исправленное выборочное среднеквадратическое отклонение случайной величины Х 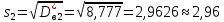 Проверяем теперь гипотезу о равенстве двух генеральных средних, т.е. гипотезу H0: 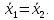 Предполагаем, что дисперсии двух выборок равны. Предполагаем, что дисперсии двух выборок равны.Поскольку мы проверяем утверждение, что среднее значение выходного параметра увеличилось, то в качестве конкурирующей выбираем гипотезу H1: 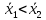 . Так как генеральные дисперсии неизвестны, а объем одной из выборок мал, используем критерий . Так как генеральные дисперсии неизвестны, а объем одной из выборок мал, используем критерий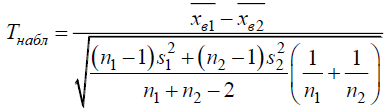 Наблюдаемое значение критерия 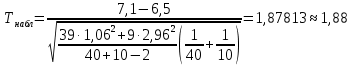 Критическую точку Tкр (2α; n1 + n2 – 2) = Tкр (0,1; 48) = 1,68 левосторонней критической области находим по таблице критических точек распределения Стьюдента при n1 + n2 – 2 степенях свободы и верности 2α. Так как Tнабл > 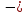 Tкр, то отвергаем нулевую гипотезу в пользу альтернативной гипотезы, т.е. утверждение об увеличении среднего значения показателя Х является Tкр, то отвергаем нулевую гипотезу в пользу альтернативной гипотезы, т.е. утверждение об увеличении среднего значения показателя Х являетсястатистически обоснованным. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||