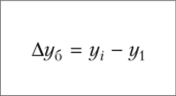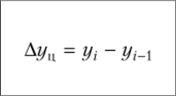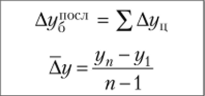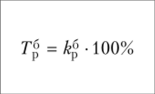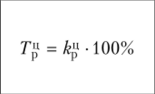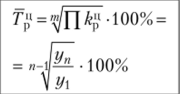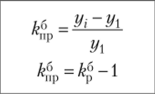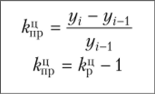Контрольная работа по Статистике Ерёмин В.М. 3П Сургут. Контрольная работа по учебной дисциплине Статистика Вариант 9 Преподаватель
 Скачать 248.72 Kb. Скачать 248.72 Kb.
|
|
Министерство образования и науки Челябинской области Государственное бюджетное образовательное учреждение профессиональная образовательная организация «Златоустовский техникум технологий и экономики» Сургутский филиал Контрольная работа по учебной дисциплине «Статистика» Вариант № 9
Сургут 2022 г. Вариант 9. 1.Понятие рядов распределения, виды рядов распределения, их значение. 2.Показатели рядов динамики, порядок их расчёта. Задача №1. Имеются следующие данные об остатках материальных ценностей на складе предприятия (руб.)
Определить на сколько рублей и на сколько процентов изменилась средняя сумма материальных ценностей на складе предприятия в 2014 году по сравнению с 2013 годом; в 2015 г. по сравнению с 2014 г.; в 2016г. по сравнению с 2015г. Задача №2. Имеются следующие данные о себестоимости и объёмах производства продукции предприятия:
Определить: а) индивидуальные и сводные индексы; б) сводный индекс физического объёма продукции; в) сводный индекс затрат на производство. Покажите взаимосвязь общих индексов. 1.Понятие рядов распределения, виды рядов распределения, их значение. Ряды распределения обычно выступают в качестве составной части сводки статистических данных, так как являются разновидностью простой группировки. Однако в ряде случаев ряды распределения приобретают самостоятельное значение. Они строятся с целью изучения состава исследуемой совокупности, ее однородности, колеблемости значений признаков и границ их изменения. На основе рядов распределения рассчитываются относительные величины структуры и средние показатели. Ряд распределения — это ряд показателей, представляющих распределение единиц совокупности по одному существенному признаку, значения которого расположены в определенной последовательности. Ряд распределения включает два элемента, это: 1) варианта (х) — значения признака; 2) вес или частота (J) — это численность отдельных групп, т.е. числа, которые показывают, сколько раз данное значение признака встречается в исследуемой совокупности. Частоты, выраженные в виде относительных величин (долях единиц, процентах), называются частостями. Замена частот частостями позволяет сопоставлять ряды распределения с разным числом наблюдений. Сумма всех частот ряда называется его численностью или объемом распределения. Ряды распределения бывают двух видов: атрибутивные и вариационные. Атрибутивные ряды распределения строятся по качественному признаку. В данном случае количество групп изучаемых единиц соответствует числу категорий значений данного признака. Например, ряд распределения населения по полу включает две группы: мужчины и женщины, а ряд распределения предприятий по формам собственности будет включать шесть групп: государственная, муниципальная, собственность общественных объединений, частная, иностранная, смешанная. Вариационные ряды распределения строятся по количественному признаку. Например, распределение населения по возрасту, рабочих — но стажу работы, заработной плате и т.д. Вариационные ряды в зависимости от характера вариации подразделяются на дискретные и интервальные. Дискретный вариационный ряд распределения — это преобразованный ранжированный ряд, в котором перечисление случаев с одинаковым значением признака заменяется его частотой. Например, известен стаж работы персонала организации: 1, 1, 1, 1, 2, 3, 3, 3, 4, 4, 5, 5, 7, 7, 7. Этот ранжированный ряд гораздо легче анализировать, если его преобразовать в ряд распределения (табл. 1). Однако приведенная форма ряда распределения применима лишь для тех случаев, когда варьирующий признак принимает небольшое количество значений. В обратном случае, когда количество значений признака бесконечно большое (десятки, сотни, тысячи), невозможно образовывать группу для каждого варианта, так как ряд распределения будет являться труднообозримым и непосредственное его рассмотрение не даст представления о распределении единиц по значению признака в совокупности. В этом случае объединение отдельных значений наблюдения в группы возможно только на базе интервала. Использование интервалов приводит к применению интервального вариационного ряда распределения. Преобразуем ранжированный ряд значений стажа работы персонала в интервальный ряд распределения (табл. 2). Таблица 1 Дискретный ряд распределения работников организации по стажу работы
Таблица 2 Интервальный ряд распределения работников организации по стажу работы
В таком виде характер вариации признака отражается гораздо отчетливее, нежели в ранжированном ряде. Рассматривая интервальный ряд распределения, сразу можно сказать, в каких группах наблюдается скопление случаев, т.е. какой вес является преобладающим. Из представленных примеров нетрудно заметить, что правила построения рядов распределения аналогичны правилам построения группировки данных. 2.Показатели рядов динамики, порядок их расчёта. Для количественной оценки динамики проводят расчет таких показателей, как абсолютный прирост, темп роста, темп прироста, темп наращивания, абсолютное значение 1% прироста, средний уровень ряда динамики. В основе расчета показателей ряда динамики лежит сравнительный анализ уровней ряда либо с постоянной, либо с переменной базой сравнения. При постоянной базе сравнения каждый уровень ряда сравнивается с одним и тем же показателем (уровнем), принятым за базу сравнения (у{). В этом случае получают базисные показатели. При переменной базе сравнения каждый уровень ряда сравнивают с предыдущим уровнем (г/м) и получают цепные показатели. Связь между ценными и базисными показателями легко представить в виде следующей схемы (рис. 1). Выделяют следующие аналитические показатели динамики (таблица 1). 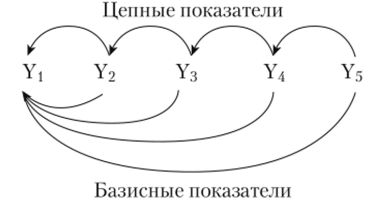 Рис. 1.Взаимосвязь цепных и базисных показателей Таблица 1 Формулы расчета и взаимосвязь показателей динамики
Условные обозначения: г, — текущий уровень ряда; у, — предыдущий уровень ряда; у{ — начальный (или базисный) уровень ряда; уп — последний уровень ряда; п — количество уровней в ряду динамики; т — количество коэффициентов роста. Кроме перечисленных в табл. 1 аналитических показателей динамики, в статистике часто рассчитывают средний уровень ряда. Средний уровень ряда динамики характеризует обобщенную величину абсолютных уровней. Методы расчета среднего уровня интервального и моментного рядов динамики различны. Для интервальных рядов динамики средний уровень за период времени определяется по формуле средней арифметической: а) при равных интервалах применяется средняя арифметическая простая: б) при неравных интервалах применяется средняя арифметическая взвешенная: 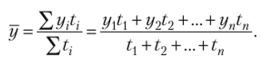 Для моментных рядов динамики средний уровень за период времени определяется по формуле средней хронологической: а) с равноотстоящими датами в ряду динамики применяется средняя хронологическая простая: 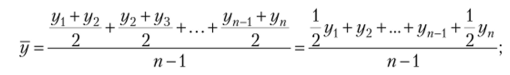 б) с равноотстоящими датами в ряду динамики применяется средняя хронологическая взвешенная: 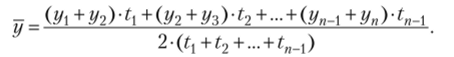 Типовая задача 1 Выпуск продукции на предприятии характеризуется следующими данными (табл. 2). 1. Определите все аналитические показатели ряда динамики. 2. Проверьте взаимосвязь цепных и базисных показателей. 3. Приведите графическое изображение динамики производственной мощности. Таблица 2 Выпуск продукции предприятием за первое полугодие, т
Решение 1. Определим аналитические показатели ряда динамики, а) абсолютный прирост: 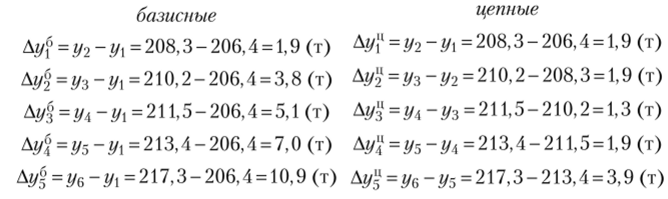 б) коэффициент роста:  в) коэффициент прироста: 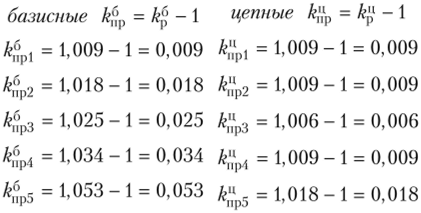 г) темп наращивания:  д) абсолютное значение 1% прироста: а = 100% 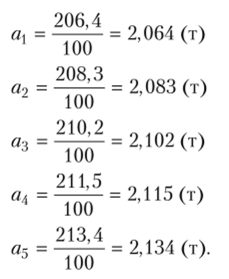 Представим полученные результаты в табличном виде (табл. 3). Анализируя полученные показатели динамики (см. табл. 3), можно сделать вывод, что по сравнению с январем объем выпуска предприятия в первом полугодии постоянно растет, но цепные показатели динамики указывают, что в апреле наблюдалось некоторое снижение объема производства продукции. Таблица 3 Аналитические показатели динамики выпуска продукции предприятием за первое полугодие
2. Проверим взаимосвязь ценных и базисных показателей: а) абсолютных приростов: Лг/"<к;| = Х*/ц. 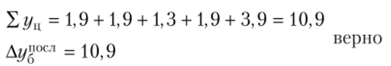 б) коэффициентов роста: k^n = П &р11- 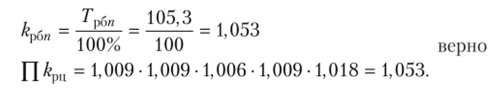 3. Графическое построение исходных данных (рис. 2). 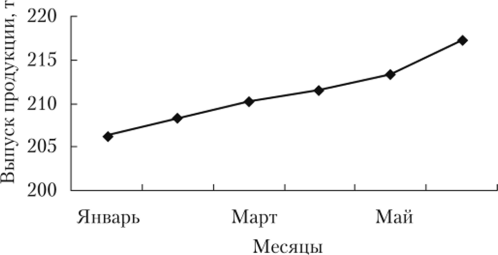 Рис. 2.Графическое изображение выпуска продукции предприятием за первое полугодие, т Задача №1. Имеются следующие данные об остатках материальных ценностей на складе предприятия (руб.)
Определить на сколько рублей и на сколько процентов изменилась средняя сумма материальных ценностей на складе предприятия в 2014 году по сравнению с 2013 годом; в 2015 г. по сравнению с 2014 г.; в 2016г. по сравнению с 2015г. Решение: Средний уровень моментного ряда динамики с равноотстоящими уровнями определяется по формуле средней хронологической моментного ряда: 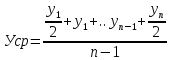 где у1,…,уn – уровни периода, за который делается расчет; n – число уровней; n–1 – длительность периода времени. Тогда: 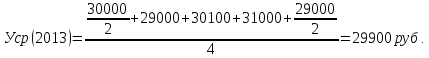 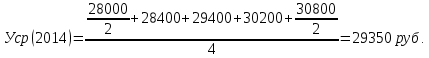 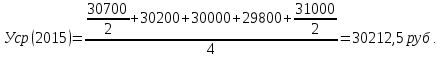 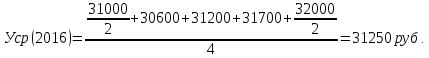 Абсолютное изменение: Δу=уi – yi-1 Тогда: в 2014 году по сравнению с 2013 годом: Δу=уi – yi-1=29350-29900= -550 руб. в 2015 году по сравнению с 2014 годом: Δу=уi – yi-1=30212,5-29350= +862,5руб. в 2016 году по сравнению с 2015 годом: Δу=уi – yi-1=31250-30212,5= +1037,5 руб. Изменение в процентах: Тпр= (уi / yi-1)*100%-100% Тогда: в 2014 году по сравнению с 2013 годом: Тпр= (29350/ 29900)*100%-100% = -1,84%. в 2015 году по сравнению с 2014 годом: Тпр= (30212,5/ 29350)*100%-100% = +2,94%. в 2016 году по сравнению с 2015 годом: Тпр= (31250/ 30212,5)*100%-100% = +3,43%. Задача №2. Имеются следующие данные о себестоимости и объёмах производства продукции предприятия:
Определить: а) индивидуальные и сводные индексы; б) сводный индекс физического объёма продукции; в) сводный индекс затрат на производство. Покажите взаимосвязь общих индексов. Решение: 1. Индивидуальные индексы: Индивидуальный индекс себестоимости: 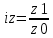 Где z1 и z0 – объем себестоимости в отчетном и базисном периоде. Индивидуальный индекс объема производства: 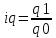 Где q1 и q0 – объем производства в отчетном и базисном периоде. Индивидуальный индекс совокупных затрат: 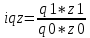 Тогда: 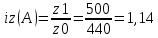 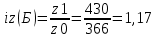 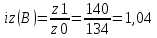 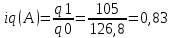 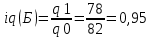 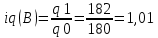 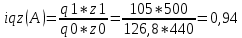 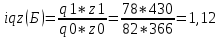 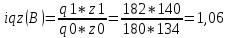 2. Сводные индексы. Сводный индекс затрат на производство: 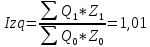 Сводный индекс физического объема: 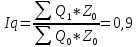 Сводный индекс себестоимости: 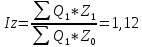 Взаимосвязь сводных индексов: 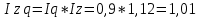 Список используемой литературы 1. Статистика Годин А.И. Учебник, М., Издательский Дом «Дашков и К», 2017 2.Статистика под редакцией к.э.н. В.Г. Ионина, - Новосибирск, изд. НГАЭ иУ, 2015 3.Статистика А.В. Сиденко, Г.Ю. Попов, В.М. Матвеева – М.: Дело и Сервис, 2016 4.Сборник задач по общей теории статистики под редакцией ред. к.э.н. Л.К. Серга, М.: Филинъ, 2015 5.Теория статистики учебник под редакцией профессора Р.А. Шмойловой. М.: Финансы и статистика, 2017 6.Практикум по теории статистики под редакцией профессора Р.А. Шмойловой – М.: Финансы и статистика, 2018 Елисеева И.И., Избашев М.М., Общая теория статистики: Учебник/ Под ред. И.И.Елисеевой–М.: Финансы и статистика,2017 г. Ефимова М.Р., Рябцев Р.М. Общая теория статистики: Учебник-М.:Финансы и статистика, 2016г. Общая теория статистики: Статистическая методология в изучении коммерческой деятельности: Учебник/Под ред. А.А Спирина, О.Э Башиной-М.: Финансы и статистика, 2016г. Практикум по статистике: Учебное пособие для вузов/Под ред.В.М. Сичмеры-М.: Финстатинформ, 2018г. Статистика : Курс лекций/Под ред.В.Г Ионина-Новосибирск :НГАЭиУ; М.: ИНФРА-М, 2017г. Теория статистики: Учебник/Под ред.Р.А. Шмойловой-М.: Финансы и статистика, 2016г. Марьянова М.Н. Сборник задач по основам статистики-М.: Финансы и статистика, 20165г. СПС «Консультант Плюс» (http://www.consultant.ru/). СПС «Гарант» (http://www.garant.ru/). | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||