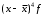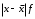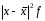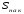Тема 6. Анализ рядов распред. 8 задач. Тема анализ рядов распределения. Методические указания Анализ рядов распределения
 Скачать 362.78 Kb. Скачать 362.78 Kb.
|
|
Тема 5. АНАЛИЗ РЯДОВ РАСПРЕДЕЛЕНИЯ. Методические указания 1. Анализ рядов распределения. Упорядоченное распределение единиц совокупности по определенному варьирующему признаку представляет собой ряд распределения. Первым этапом статистического изучения вариации количественного признака является построение вариационного ряда, который в зависимости от характера представления варьирующего признака может быть: а) интервальным; б) дискретным. Если же признак атрибутивный или альтернативный, то, соответственно, строятся атрибутивный или альтернативный ряды распределения. Для анализа вариационных рядов используется три группы показателей: структурные характеристики ряда распределения; показатели меры вариации; показатели формы распределения. Структурные характеристики ряда распределения. К ним относятся медиана ( 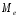 ),мода ( ),мода (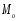 ), квартили ( ), квартили (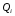 ), децили ( ), децили (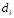 ) и перцентили ( ) и перцентили (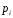 ) распределения. ) распределения.Медиана – это величина варьирующего признака, которая делит ряд распределения на две равные части, т.е. медиана соответствует варианте, стоящей в середине ряда. Медиана определяется в зависимости от вида ряда распределения: в ранжированном ряду с нечетным числом уровней медиана соответствует признаку с порядковым номером: 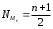 , , где n - объем совокупности. в ранжированном ряду с четным числом значений варьирующего признака ( 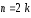 ; ;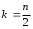 ) за медиану условно принимают значение: ) за медиану условно принимают значение: 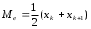 в дискретном ряду распределения медиана соответствует варианте, для которой первая накопленная частота больше половины общего числа наблюдений; в интервальном ряду распределения медианным интервалом будет интервал, для которого первая накопленная частота больше половины объема совокупности, а сама медиана определяется по формуле: 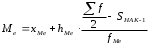 , ,где 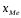 - нижняя граница медианного интервала; - нижняя граница медианного интервала;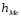 - величина медианного интервала; - величина медианного интервала;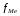 - частота медианного интервала; - частота медианного интервала; 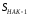 - накопленная частота до медианного интервала. - накопленная частота до медианного интервала.Графически медиана определяется по кумуляте распределения (рис. 5.2, пример 1). Мода - наиболее часто встречающийся признак в совокупности. Определяется: в дискретном ряду – по максимальной частоте; в интервальном ряду модальный интервал определяется по максимальной частоте, а сама мода - по формуле: 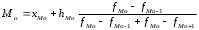 , ,где 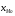 - нижняя граница модального интервала; - нижняя граница модального интервала; 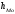 - величина модального интервала; - величина модального интервала;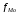 - частота модального интервала; - частота модального интервала;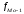 - час-тота интервала, предшествующего модальному; - час-тота интервала, предшествующего модальному;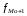 - частота интервала, следующего за модальным. - частота интервала, следующего за модальным.Графически мода определяется на основе полигона распределения (для дискретного вариационного ряда) или гистограммы распределения (для интервального вариационного ряда) (рис.5.1, пример 1). Значения признака, делящие совокупность на четыре равные части, называются квартелями и обозначаются буквой Qс подписным значком номера квартиля, - ясно, что Q2 совпадает с медианой, т.е. Q2 = = Ме. Первый (Q1) и третий (Q3) квартили определяются по следующим формулам: 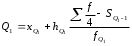 ; ; 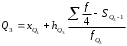 , ,гдехQ1,хQ3- нижняя граница, соответственно, первого и третьего квартильных интервалов;hQ1, hQ3- величина соответствующего первого и третьего квартильных интервалов;fQ1, fQ3- частота соотвествующих квартильных интервалов; 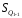 - накопленная частота до первого квартильного интервала; - накопленная частота до первого квартильного интервала;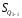 - накопленная частота до третьего квартильного интервала. - накопленная частота до третьего квартильного интервала.Децили – варианты, делящие ряд распределения на десять равных частей. Вычисляются они по той же схеме, что и медиана, и квартили: 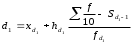 ; ;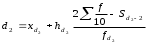 и т.д и т.дЗначения признака, делящее ряд на сто частей, называются перцентилями, и их расчет выполняется аналогично исчислению децилей и квартилей. Анализ вариационного ряда дополняется определением показателей дифференциации и концентрации. Например, коэффициент децильной дифференциации: 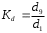 , гдеd9 – девятая дециль, или девятый дециль;d1 – первая дециль, или первый дециль. , гдеd9 – девятая дециль, или девятый дециль;d1 – первая дециль, или первый дециль.Он показывает, во сколько раз наименьший уровень признака из 10% признаков, имеющих наибольший уровень, больше наибольшего уровня признака из 10% единиц совокупности, имеющих наименьший уровень признака. Коэффициент фондов (Кф)– это соотношение между средними значениями изучаемого признака (или суммарными их значениями) в десятой и первой децильных группах, - рассчитывается по формуле: 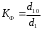 Показатели меры вариации. Количественная оценка степени ко-леблемости признака в совокупности измеряется с помощью показателей вариации. Различают абсолютные и относительные показатели вариации. Абсолютные показатели вариации: 1. Размах вариации: 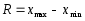 , ,где 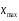 , ,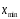 - соответственно, наибольшее и наименьшее значение варьирующего признака. - соответственно, наибольшее и наименьшее значение варьирующего признака. 2. Среднее линейное отклонение: 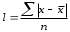 - простое; - простое; 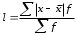 - взвешенное. - взвешенное.3. Дисперсия: 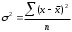 - простая; - простая; 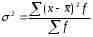 - взвешенная. - взвешенная.4. Среднее квадратическое отклонение: 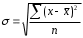 - простое; - простое; 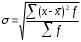 - взвешенное. - взвешенное.Среднее квадратическое отклонение и среднее линейное отклонение – это обобщающие характеристики размеров вариации признака в совокупности, они выражаются в тех же единицах измерения, что и сам признак. При сравнительно простых значениях признака используется упрощенный способ расчета дисперсии и среднего квадратического отклонения – метод разности средних: 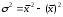 ; ; 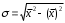 . .по несгруппированным данным: 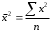 ; ; 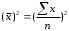 , , по сгруппированным данным: 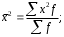 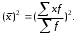 Относительные показатели вариации: Относительный размах вариации или коэффициент осцилляции (КR): 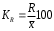 ; ;Относительное линейное отклонение или линейный коэффициент вариации (К 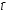 ): ): 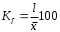 ; ;Коэффициент вариации (V): 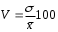 . .Средняя и дисперсия альтернативного признака. Введем условные обозначения для альтернативного признака и построим альтернативный ряд распределения. Альтернативный признак принимает значение 1, что означает наличие признака; 0 – его отсутствие; р – доля единиц, обладающих данным признаком, q – соответственно, необладающих данным признаком. Тогда среднее значение альтернативного признака будет равно: 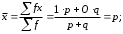 при этом p + q = 1, т.е. q =1 – p. при этом p + q = 1, т.е. q =1 – p.Дисперсия и среднее квадратическое отклонение рассчитываются по соотношению: 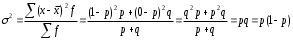 /. /. 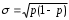 . .Показатели формы распределения. Для получения приблизительного представления о форме распределения строят графики распределения (полигон и гистограмму), рассчитываются структурные или ранговые характеристики распределения (квартили, децили), показатели дифференциации, концентрации, асимметрии, эксцесса, а также строятся кривые распределения. Для сравнительного анализа степени асимметрии нескольких распределений рассчитывается показатель асимметрии (АS): 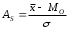 или или 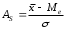 Наиболее широко (как показатель асимметрии) применяется отношение центрального момента третьего порядка (m3) к среднему квадратическому отклонению в кубе, т.е. 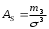 , ,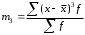 . .Если 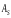 > 0,то это указывает на наличие правосторонней асимметрии, а при > 0,то это указывает на наличие правосторонней асимметрии, а при 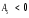 , - левосторонней. Чем больше абсолютная величина коэффициента, тем больше степень скошенности распределения. , - левосторонней. Чем больше абсолютная величина коэффициента, тем больше степень скошенности распределения.Оценка существенности AS проводится на основе средней квад-ратической ошибки коэффициента ( 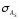 ): ):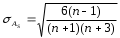 . .Если 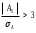 , асимметрия распределения существенна и распределение признака в генеральной совокупности несимметрично. В противном случае асимметрия несущественна, и ее наличие может быть вызвано случайными факторами. , асимметрия распределения существенна и распределение признака в генеральной совокупности несимметрично. В противном случае асимметрия несущественна, и ее наличие может быть вызвано случайными факторами.Для симметричных распределений рассчитывается показатель эксцесса (островершинности): 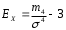 , ,где m4 – центральный момент четвертого порядка; m4 = 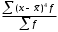 . .Эксцесс у высоковершинных распределений положительный, а у низковершинных – отрицательный. Появление значительного отрицательного эксцесса может указывать на качественную неоднородность исследуемой совокупности. Для оценки существенности коэффициента эксцесса используется его средняя квадратическая ошибка ( 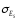 ): ):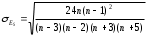 . .Если 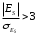 , то значение коэффициента эксцесса существенно или статистически значимо. , то значение коэффициента эксцесса существенно или статистически значимо.Решение типовых задач Пример 1. Имеются следующие данные об успеваемости студентов факультета по статистике: 4, 2, 5, 5, 3, 4, 3, 2, 5, 5, 4, 4, 3, 3, 4, 2, 1, 1, 1, 3, 4, 4, 4, 5, 5, 4, 2, 2, 3, 3. Для анализа распределения студентов по успеваемости: 1) постройте дискретный ряд распределения; 2) дайте графическое изображение ряда; 3) исчислите структурные средние ряда (двумя способами) и показатели формы распределения; 4) проверьте гипотезу о соответствии эмпирического распределения нормальному закону распределения. Решение Для построения дискретного вариационного ряда необходимо подсчитать количество появления каждой оценки, т.е. частоту появления признака. Дискретный ряд представлен в таблице 5.1. Таблица 5.1 Распределение студентов по успеваемости
Графически дискретный вариационный ряд может быть представлен в виде полигона (рис.5.1), кумуляты (рис.5.2) распределения. Полигон строится в прямоугольной системе координат.                                         f 9 6 5 7 3 полигон х 1,72 4 3 1 3,93  число студентов, чел  Мо= 4(балла)    успеваемость, балл 5 2  полигон распределения теоретическая кривая нормального распределения Рис. 5.1. Распределение студентов по успеваемости. По оси абсцисс откладываются значения дискретного признака, а по оси ординат – частоты распределения. Полигон часто замыкается, - для этого крайние вершины соединяются с точками на оси абсцисс, отстоящими на одно деление в принятом масштабе (в данном примере х = 0 и х = 6). Кумулята – это линейный график накопленных частот. Для построения кумуляты дополнительно рассчитываются накопленные частоты (SНАК), - они представлены в таблице 5.1, и в прямоугольной системе координат строится их график (рис.5.2). 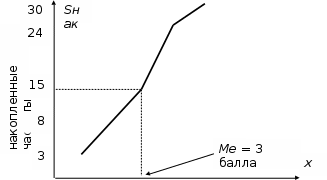       1 2 3 4 5 успеваемость,балл Рис. 5.2. Кумулята распределения студентов по успеваемости 3. Cтруктурными средними выступают мода и медиана. Модальное значение признака, т.е. Мо = 4 (балла). Графически – это вершина полигона распределения (рис.5.1). Медиана равна 3 балла, так как SНАК = 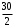 =15 для признака, равному 3. Графически медиана определяется с помощью кумуляты распределения. Для ее определения сумму ординат (сумму частот) делят пополам, т.е. =15 для признака, равному 3. Графически медиана определяется с помощью кумуляты распределения. Для ее определения сумму ординат (сумму частот) делят пополам, т.е.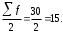 . Через полученную точку проводится прямая параллельно оси абсцисс до пересечения ее с кумулятой. Абсцисса точки пересечения является медианной величиной распределения (рис. 5.2). . Через полученную точку проводится прямая параллельно оси абсцисс до пересечения ее с кумулятой. Абсцисса точки пересечения является медианной величиной распределения (рис. 5.2).Для оценки формы распределения исчислим коэффициент асимметрии и эксцесса: 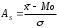 ; ;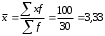 (балла); М0== 4(балла); (балла); М0== 4(балла);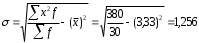 ; ;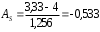 . .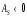 , это свидетельствует о наличии левосторонней асимметрии распределения студентов по успеваемости (рис. 5.1). , это свидетельствует о наличии левосторонней асимметрии распределения студентов по успеваемости (рис. 5.1).Для проверки статистической гипотезы о существенности асимметрии рассчитываем соотношение 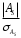 , исчислив предварительно: , исчислив предварительно: 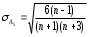 = =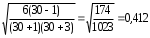 ; ; 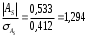 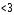 . . В нашем примере наличие асимметрии несущественно и объясняется влиянием случайных факторов. Исчислим коэффициент эксцесса: 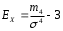 ; ; 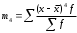 = =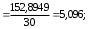 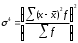 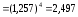 ; ; 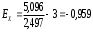 . .Так как 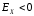 , то распределение студентов по успеваемости – низковершинное или плосковершинное по сравнению с нормальным распределением. , то распределение студентов по успеваемости – низковершинное или плосковершинное по сравнению с нормальным распределением.Пример 2. Известно распределение коммерческих банков области по размеру прибыли.
Оцените уровень вариации банков по размеру прибыли, рассчитав абсолютные и относительные показатели вариации. Сделайте выводы. Решение 1. Для определения абсолютных показателей вариации необходимо закрыть открытые интервалы и перейти от интервального ряда к дискретному (табл.5.2. гр. 3) Таблица 5.2 Вспомогательные расчеты для определения показателей вариации
Рассчитываем следующие абсолютные показатели вариации: размах вариации (R); среднее линейное отклонение ( 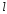 ), дисперсию ( ), дисперсию (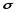 ). ).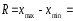 60 – 0= = 60 (млн. грн.) Размер отклонений величины максимальной прибыли от минимальной по всей совокупности банков составляет 60 млн.грн. 60 – 0= = 60 (млн. грн.) Размер отклонений величины максимальной прибыли от минимальной по всей совокупности банков составляет 60 млн.грн.Для расчета 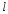 и и 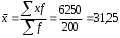 млн.грн; млн.грн; 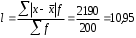 млн.грн. млн.грн.Индивидуальные размеры прибыли в среднем по всей совокупности банков отклонялись в ту и другую сторону от своего среднего значения на 10,95 млн. грн. Дисперсию определим двумя способами: по формуле среднего квадрата отклонений 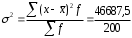 = = 233,44 = = 233,44по формуле “разности средних”: 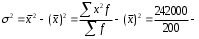 - (31,25) 2 = 1210 – 976,56 = 233,44. Среднее квадратическое отклонение: 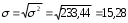 млн.грн. млн.грн.Размеры прибыли каждого из 200 банков отклонялись в ту и другую сторону от среднего значения на 15,28 млн. грн. Определим теперь относительные показатели вариации: коэффициент осцилляции: 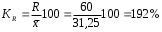 ; ;относительное линейное отклонение: 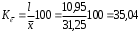 %; %;коэффициент вариации: 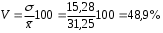 Анализируемый вариационный ряд распределения банков по размеру прибыли является статистически неоднородным, так как коэффициент вариации больше 33%. Об этом свидетельствует другие показатели вариации, например, коэффициент осциляции показывает, что разность между крайними значениями признака почти в 2 раза больше ( 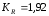 или 192 %) их среднего значения. или 192 %) их среднего значения.Среднее значение показателя прибыли по данной совокупности банков ( 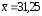 тыс.грн) не является надежной или типической ее характеристикой. тыс.грн) не является надежной или типической ее характеристикой.Пример 3. Распределение семей по среднедушевым доходам следующее (таблица 5.3). Определите: 1. а) структурные характеристики распределения семей по размеру среднедушевого дохода; б) показатели формы и дифференциации распределения. 2. Постройте график эмпирического и теоретического распределения семей по размеру среднедушевого дохода. Решение 1а. Определяем структурные характеристики ряда распределения, т.е. моду медиану, квартили, децили по рассмотренным выше формулам этих характеристик для интервальных вариационных рядов. Для выбора соответствующего интервала предварительно опре-делим накопленные частоты 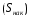 , (табл. 5.4, гр. 4). , (табл. 5.4, гр. 4).Модальный интервал – это интервал с наибольшей частотой 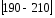 , тогда , тогда 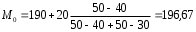 грн. грн.Большинство семей имеют среднедушевые доходы в размере 196,67 грн. Медианным является интервал 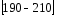 , т.к. для него первая накопленная частота больше половины объема совокупности, т.е. 120100. Тогда медиана будет равна: , т.к. для него первая накопленная частота больше половины объема совокупности, т.е. 120100. Тогда медиана будет равна: 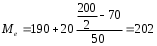 грн. грн.Половина семей имеют среднедушевые доходы, не превышаю-щие доходы 202 грн., а у другой половины семей среднедушевые доходы, соответственно, выше 202 грн. Интервал, в котором будет находиться первый квартиль( 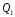 ) рас-пределения, ) рас-пределения, 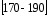 , т.к. ему соответствует первая накопленная час-тота , т.к. ему соответствует первая накопленная час-тота 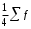 ; а интервал, в котором находится третий квартиль( ; а интервал, в котором находится третий квартиль(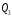 ), будет ), будет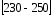 , т.к. ему соответствует , т.к. ему соответствует 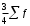 . .Тогда соответствующие квартили будут равны: 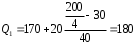 грн; грн; 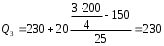 грн. грн.Среднедушевые доходы, не превышающие 180 грн., получают не менее четверти (25%) из всей совокупности семей, а в размере, не превышающем 230грн., не менее 75% всех семей. Более детальная характеристика распределения может быть получена на основе децилей распределения. Интервалы соответствующих децилей определяются аналогично по соответствующим накопленным частотам. Например, находим первую  , - это будет , - это будет 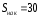 ; тогда соответствующий ей интервал ; тогда соответствующий ей интервал 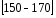 будет тем интервалом, в котором находится первый дециль (d1) – и т.д. будет тем интервалом, в котором находится первый дециль (d1) – и т.д.Рассчитаем соответствующие децили: 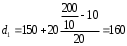 грн; грн; 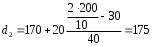 грн; грн;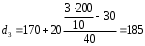 грн; грн; 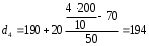 грн; грн;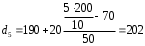 грн; грн; 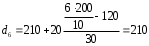 грн; грн;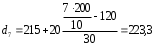 грн; грн; 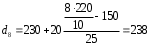 грн; грн;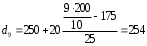 грн. Первый дециль показывает, что у 10% семей с самым низким среднедушевым доходом самый высокий размер среднедушевого дохода составляет 160 грн., а девятый дециль, - что среди 10% семей с самым высоким уровнем дохода – нижняя его граница составляет 254 грн. грн. Первый дециль показывает, что у 10% семей с самым низким среднедушевым доходом самый высокий размер среднедушевого дохода составляет 160 грн., а девятый дециль, - что среди 10% семей с самым высоким уровнем дохода – нижняя его граница составляет 254 грн.Таблица 5.3 Распределение семей по среднедушевому доходу
Пример 4. Налоговой инспекцией одного из районов города проверено 172 коммерческих киоска и в 146 из них выявлены финансовые нарушения. Определите среднее значение, дисперсию и среднее квадратическое отклонение альтернативного признака, т.е. доли киосков, у которых выявлены финансовые нарушения. Решение Определяем долю коммерческих киосков, у которых выявлены финансовые нарушения: 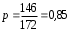 . Тогда доля киосков, у которых отсутствуют финансовые нарушения, будет: . Тогда доля киосков, у которых отсутствуют финансовые нарушения, будет: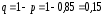 . .Среднее значение альтернативного признака: 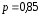 . Дисперсия альтернативного признака составит: . Дисперсия альтернативного признака составит: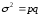 = 0,85 · 0,15 = 0,128, а среднее квадратическое отклонение: = 0,85 · 0,15 = 0,128, а среднее квадратическое отклонение: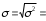 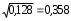 . .Задачи для самостоятельного решения Каждый должен решить ОДНУ любую задачу из восьми предложенных 5.1. По имеющимся данным о производстве изделий двумя бригадами рабочих определите для каждой бригады: размах вариации, среднее линейное отклонение, дисперсию, коэффициент вариации.
5.2. На основе данных об урожайности ржи и размерах посевных площадей определите дисперсию и среднее квадратическое отклонение (двумя способами) и коэффициент вариации; моду и медиану.
5.3. Из 150 выпускников средней школы 20 человек получили золотые и серебряные медали. Определите: дисперсию, среднее квадратическое отклонение и коэффициент вариации доли медалистов. 5.4. Имеются следующие данные о размере семей в районе (по числу человек в семье): 3, 4, 5, 7, 2, 1, 4, 6, 6, 5, 5, 7, 7, 1, 1, 1, 2, 2, 2, 2, 3, 3, 4, 4, 5, 6, 6, 1, 3, 3, 5, 5, 6, 2, 2, 3, 3, 4, 4, 2. Составьте дискретный вариационный ряд. Определите структурные средние распределения. Дайте графическое изображение ряда. 5.5. По данным об успеваемости по статистике студентов двух групп определите, в какой группе более ровная успеваемость студентов.
5.6. Распределение студентов одного из факультетов по возрасту характеризуется данными:
Определите: 1) средний возраст студентов факультета; 2) показатели вариации (размах вариации, среднее линейное отклонение, дисперсию, среднее квадратическое отклонение, коэффициент вариации); 3) коэффициент асимметрии. Крестьянские хозяйства района подразделяются по размерам земельных наделов следующим образом:
Исчислите: 1) абсолютные и относительные показатели вариации; 2) структурные характеристики распределения хозяйств по размерам земельных наделов. 5.8. В трех партиях продукции, представленных на контроль качества, было обнаружено: а) первая партия – 1000 изделий, из них 800 годных; б) вторая партия – 800 изделий, из них 720 годных; в) третья партия – 900 изделий, из них 850 годных Определите в целом по трем партиям дисперсию, среднее квадратическое отклонение и коэффициент вариации годной продукции. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||