Контрольная работа «План теодолитной съёмки». демо версия. Контрольная работа по учебному курсу Геодезия 1 (наименование учебного курса) Вариант 9 Студент Иванов И. И
 Скачать 218.64 Kb.
|
|
М  ИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИфедеральное государственное бюджетное образовательное учреждение высшего образования «Тольяттинский государственный университет» Архитектурно-строительный институт (наименование института полностью) Центр архитектурных, конструктивных решений и организации строительства (наименование кафедры/департамента/центра полностью) 08.03.01 Строительство (код и наименование направления подготовки, специальности) Промышленное и гражданское строительство (направленность (профиль) / специализация) Контрольная работа по учебному курсу «Геодезия 1» (наименование учебного курса) Вариант 9
Тольятти 2023 Контрольная работа «План теодолитной съёмки»Вычисление угловой невязки теодолитного хода Вычислим угловую невязку замкнутого хода в соответствии с формулой: fβ= Σβизм – Σβтеор, Σβизм =78˚04.5'+120˚35.5'+84˚50.5'+76˚28' = 358˚58.5'; Σβтеор=180˚(n – 2) = 360˚, fβ= 358˚58.5' – 360˚ = –0˚01.5'. Вычисляем предельно допустимую невязку внутренних углов: fβ доп = ± 2 · 30''  = ±2'Таким образом, полученная угловая невязка не превышает предельно допустимой погрешности (|-01.5'| < 2’) и распределяется равномерно по измеренным горизонтальным углам. Величины поправок подписаны над значениями минут соответствующих измеренных углов. Результаты введения поправок записываем в графу исправленных горизонтальных углов с точностью до десятых долей угловой минуты. Сумма исправленных внутренних углов равна 360˚, следовательно, поправки введены верно. Вычисление дирекционных углов сторон хода: αi+1=αi+180°- βпр где βпр. – правые внутренние исправленные углы. 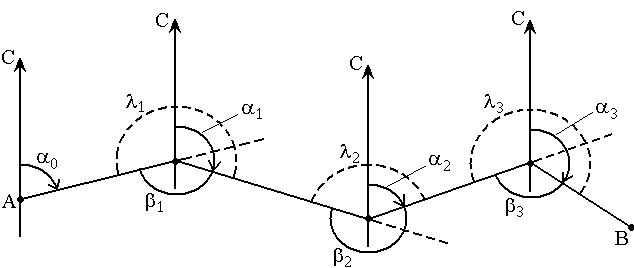 Рисунок. 1 Схема вычисления дирекционных углов α2-3 = 27°19’ +180° - 78°04.9’ = 129°14.1'; α3-4 = 129°14.1' +180° - 120°35.9’ = 188°38.2' и т.д. Контроль вычисления дирекционных углов соблюден – в конце вычислений получен начальный дирекционный угол α1-2. Вычисленные значения дирекционных углов всех сторон занесены в одноименную графу. Вычисление румбов сторон. Перевод дирекционных углов в румбы выполняется по таблице 1. Таблица 1 Зависимость дирекционных углов и румбов
α1-2 = 27°19’→0° < α1-2 < 90°, r1-2= 27°19’ (СВ); α2-3= 129°14.1'→90° < α2-3 < 180°, r2-3=180°–129°14.1'=50°45.9' (ЮВ) и т.д. Вычисление приращений координат (∆Х, ∆У) Приращения координат теодолитного хода вычисляем в соответствии с формулами прямой геодезической задачи: ΔХ = d·cosr, ΔУ = d·sinr. где d – горизонтальное проложение стороны хода; r – румб. Знаки приращений принимаются в зависимости от четверти румба согласно таблицы 1. ΔХ1-2 = 146.32·cos27°19’ = +112.99 м (  );ΔУ1-2 = 146.32·sin27°19’ = +92.97 м ( );ΔХ2-3 = 71.91·cos50°45.9' = -56.17 м ( 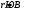 );ΔУ2-3 = 71.91·sin50°45.9' = +44.89 м ( 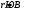) и т.д.Результаты вычислений занесены в графы Вычисленные приращения координат Вычисление невязок координат (fx, fy) По полученным значениям приращений координат вычисляем линейные невязки по осям x и у: f х = ΣΔХвыч – ΣΔхтеор; f у = ΣΔУвыч – ΣΔутеор. Так как теритическая сумма приращений по обеим осям равна нулю, то значения невязок равны сумме вычисленных приращений. Значение сумм записывают внизу граф вычисленных приращений. В нашем примере линейные невязки равны: f х = 0.10 м и f у = -0.05 м. Невязки в приращениях координат обусловлены действием погрешностей измерения углов и сторон хода. Совместное влияние невязок приращений по осям координат характеризуется линейной невязкой в периметре. Эту невязку называют абсолютной невязкой fабс.: fабс = 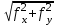 fабс =  =0.11м.Допустимую линейную невязку (ее называют относительной невязкой) вычисляют по формуле: fотн = 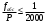 .Так как в нашем случае 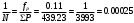 , то можно считать, что линейные измерения, как и угловые, были выполнены с достаточной точностью.Полученные значения линейных невязок распределяем между приращениями пропорционально длинам сторон с учетом знаков приращений и невязок, в соответствии с формулами: | |||||||||||||||||||||||||||||||||||||||||