Конспект лекций по инженерной геодезии. Лекции по инженерной геодезии для заочной форм обучения направлений 270100 Строительство, 270200 Транспортное строительство
 Скачать 3.15 Mb.
|
|
Министерство образования и науки РФ Государственное образовательное учреждение Высшего профессионального образования Тульский государственный университет Кафедра геоинженерии и кадастра ЛЕКЦИИ ПО ИНЖЕНЕРНОЙ ГЕОДЕЗИИ для заочной форм обучения направлений: 270100 – «Строительство», 270200 – «Транспортное строительство». Специальностей: 270102 – «Промышленное и гражданское строительство»; 270106 – «Производство строительных материалов, изделий и конструкций»; 270109 – «Теплогазоснабжение и вентиляция»; 270112 – «Водоснабжение и водоотведение»; 270105 – «Городское строительство и хозяйство». ТУЛА 2011 Лекция 1 Предмет и задачи геодезии, методы геодезических исследований Инженерная геодезия в строительстве Геодезия (греч. gedaisa, от ge – Земля и daio – делю, разделяю), наука об определении положения объектов на земной поверхности, о размерах, форме и гравитационном поле Земли и других планет. Это отрасль прикладной математики, тесно связанная с геометрией, математическим анализом, классической теорией потенциала, математической статистикой и вычислительной математикой. В то же время это наука об измерениях, разрабатывающая способы определения расстояний, углов и силы тяжести с помощью различных приборов. На протяжении веков задачи геодезии усложнялись и теперь геодезию определяют как науку, изучающую фигуру и гравитационное поле Земли и их эволюцию во времени. Геодезия разрабатывает способы определения положения точек в различных системах координат. Она занимается точными измерениями на местности для создания карт и планов и решения многообразных инженерных задач. Основная задача геодезии – создание системы координат и построение опорных геодезических сетей, позволяющих определить положение точек на земной поверхности. В этом существенную роль играют измерения характеристик гравитационного поля Земли, связывающие геодезию с геофизикой, использующей гравиметрические данные для изучения строения земных недр и геодинамики. Усложнение и развитие геодезии привело к разделению ее на несколько научных дисциплин. Высшая геодезия изучает фигуру Земли, ее размеры и гравитацонное поле, обеспечивает распространение принятых систем координат в пределах государства, континента или всей поверхности Земли, занимается исследованием древних и современных движений земной коры, а также изучает фигуру, размеры и гравитационное поле других планет Солнечной системы. Топография изучает методы топографической съемки местности с целью изображения ее на планах и картах. Картография изучает методы и процессы создания и использования карт, планов, атласов и другой картографической продукции. Фотограмметрия (фототопография и аэрофототопография) изучает методы создания карт и планов по фото- и аэрофотоснимкам. Маркшейдерия (подземная геодезия) изучает методы проведения геодезических работ в подземных горных выработках. Инженерная геодезия изучает методы и средства проведения геодезических работ при изысканиях, проектировании, строительстве и эксплуатации различных инженерных сооружений. Четко обозначенных границ между перечисленными дисциплинами нет. Так, топография включает в себя элементы высшей геодезии и картографии, инженерная геодезия использует разделы практически всех остальных геодезических дисциплин и т.д. В последние годы строительство так называемых уникальных инженерных сооружений потребовало от геодезии резкого повышения точности измерений. Так, при монтаже оборудования мощных ускорителей приходится учитывать десятые и даже сотые доли миллиметра. По результатам геодезических измерений изучают деформации и осадки действующего промышленного оборудования, обнаруживают движение земной коры в сейсмоактивных зонах, наблюдают за уровнями воды в реках, морях и океанах и уровнем грунтовых вод. Краткая история развития геодезии и современные технологии Самостоятельное изучение. Литература: Лекции по инженерной геодезии (с фрагментами методического комплекса). Учебное пособие/ В.П. Абрамов; под редакцией О.С. Разумова. – Тула, 2005. С 8–9. Современное представление о фигуре Земли Земли принято считать замкнутую поверхность, образованную средним уровнем океанов и морей, мысленно продолженную под материками. Такая фигура, по предложению немецкого ученого Листинга (XIX в), была названа геоидом. Поверхность геоида в каждой своей точке перпендикулярна к отвесной линии (вектору силы тяжести), то есть она всюду горизонтальна. Эта поверхность называется уровенной, и ей соответствует некоторое постоянное значение потенциала силы тяжести. Фигурой геоида вследствие неравномерного распределения масс в теле Земли имеет сложную неправильную форму и ее трудно описать замкнутыми математическими выражениями. Горизонтальных поверхностей, перпендикулярных направлению силы тяжести, можно провести на разных уровнях множество. А так как средний уровень океана нигде не зафиксирован, то геоидом также называют уровенную поверхность поля силы тяжести, проходящую через точку начала отсчета высот. В России такой точкой служит нуль Кронштадтского футштока. По внешнему виду геоид близок к фигуре эллипсоида вращения (сфероиду) и для решения геодезических задач и создания системы геодезических координат подбирают такие параметры эллипсоида, и так располагаю его в теле Земли, чтобы его поверхность была наиболее близка к поверхности геоида. Такой эллипсоид называют общеземным. А эллипсоид вращения определенных размеров, некоторым образом ориентированный в теле Земли так, чтобы отступление его от поверхности геоида были минимальными в пределах данной страны (или группы стран), называют референц-эллипсоидом (рекомендованным эллипсоидом). Для территории России (СССР) с 1946 г. используется референц-эллипсоид Ф. Н. Красовского (рис. 1.), параметры которого определяются большой полуосью а = 6378245 м., малой полуосью b = 6356253 м. и полярным сжатием α = (а – b)/а = 1/298,3. Параметры нашего референц-эллипсоида близки к параметрам международного общеземного эллипсоида, для которого а = 6378136 м и α =1/298,26. 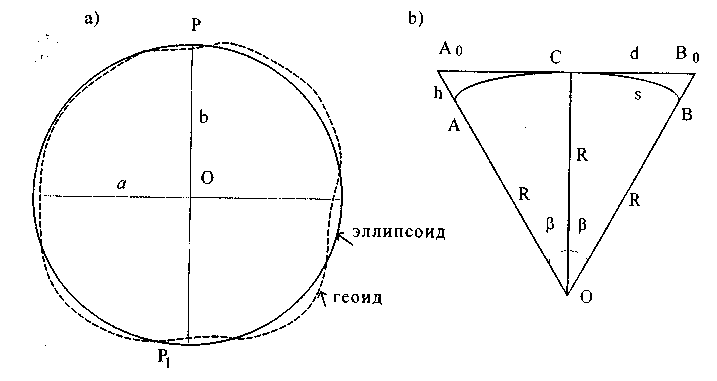 Рис. 1. Фигура Земли (а) и влияние кривизны на измеренные расстояния и превышения (б) Уменьшеннoe и подобное изображение небольших участков местности на плоскости называют планом местности. Масштаб плана во всех точках одинаков. При изображении больших участков местности на плоскости нельзя обойтись без искажении длин линий и углов, так как шар без разрывов не развёртывается на плоскость. Поэтому уменьшенное, обобщенное и построенное по определенным математическим законам (законам картографических проекций) изображение значительных участков земной поверхности на плоскости называется картой. Масштаб карты в разных точках различен; он сохраняется только по некоторым главным направлениям (обычно вдоль отдельных меридианов и параллелей) и этот масштаб называется главным. На карту наносят сетку геодезических координат – линий меридианов и параллелей. Меридианом называют воображаемую линию на Земле, образованную секущей плоскостью, проходящей через ось вращения Земли. Начальным меридианом принято считать меридиан, проходящий через Гринвичскую обсерваторию в Англии. Параллель - воображаемая линия, образованная на поверхности Земли секущей плоскостью, перпендикулярной оси вращения Земли. Параллель, проходящая через центр Земли, называется экватором. По своему назначению карты бывают трёх видов - общегеографические, топографические и тематические. Общегеографические карты обычно составляются в мелких масштабах. Общегеографические карты масштаба 1:1000000 и крупнее называют топографическими. В содержание этих карт входит рельеф, гидрография, населенные пункты, пути сообщения, объекты промышленности, сельского хозяйства и культуры. На карты наносят также границы административного деления. Топографические карты служат основой для архитектурно-планировочных работ, а тематические используются для планирования рационального размещения застройки, систем транспорта, озеленения и других работ. Тематические карты отличаются специальной направленностью своего содержания. Карты природных условий бывают геологические, почвенные, гидрогеологические, климатические с показом ветрового режима, влажности, загазованности воздуха и загрязнения почвы. Системы координат применяемые в геодезии Для определения положения точек в масштабе всей Земли в геодезии используют три системы координат – астрономическую, геодезическую и геоцентрическую пространственную прямоугольную систему. Астрономические координаты - это угловые величины и определяющие положение точек земной поверхности относительно земного экватора и начального меридиана. 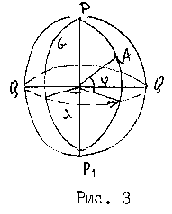 Рис. 2 Астрономическая широта- φ - это угол, составляемый направлением отвесной линии в данной точке с плоскостью земного экватора. Широты отсчитываются к северу и югу от экватора и соответственно называются северными и южными. Астрономическая долгота λ - это двугранный угол между плоскостью начального меридиана и плоскостью меридиана данной точки. Долготы отсчитываются на восток и на запад от начального меридиана и называются восточными и западными. Астрономические координаты могут, определятся из астрономических наблюдений. Координаты геодезические определяют положение точек земное поверхности на референц-эллипсоиде. Геодезическая широта В - угол, составленный направлением нормали к референц-эллипсоиду в данной точке с плоскостью геодезического экватора. Геодезическая долгота L - двугранный угол между плоскостью геодезического меридиана данной точки и плоскостью начального меридиана. Геодезические координаты вычисляются по результатам наземных геодезических измерений, спроектированных на поверхность референц-эллипсоида. При составлении планов и карт местности обычно используется левая система плоских прямоугольных координат (рис. 3). 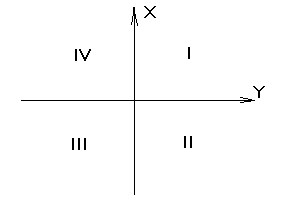 Рис.3 В этой системе вертикальная линия, ориентируемая на север, является осью абсцисс, а горизонтальная направлением на восток - осью ординат. Нумерация четвертой здесь идёт по ходу часовой стрелки; знаки функций те же, что я в левой системе плоских прямоугольных координат. Если ось абсцисс совмещается с более выгодным направлением, то такая система координат называется условной. Системы высот. Для определения высот точек Земли относительно некоторой отсчетной уровенной поверхности используется несколько систем высот. Высотой (отметкой, альтитудой) точки называют расстояние, измеренное по отвесной линии от отсчетной уровенной поверхности до данной точки. Абсолютная (ортометрическая) высота H отсчитывается от поверхности геоида, относительная (условная) H – от произвольной уровенной поверхности, геодезическая – от поверхности референц-эллипсоида (рис.4). В России за начало отсчета высот принят средний уровень Балтийского моря в районе Кронштадского футштока, и наша система высот называется Балтийской (нормальной). В ней отсчетной поверхностью служит квазигеоид – фигура, близкая к поверхности геоида. Балтийская система в пределах одного метра отличается от Адриатической системы (Австрия) и Северной (Германия). Сам уровень Балтийского моря выше уровня Черного моря на 0,7 м и, что самое любопытное, близкие друг к другу уровни Тихого и Атлантического океанов в районе Панамского канала отличаются по высоте на 0,6 м. Все это следует иметь в виду при использовании картографических материалов разных стран. 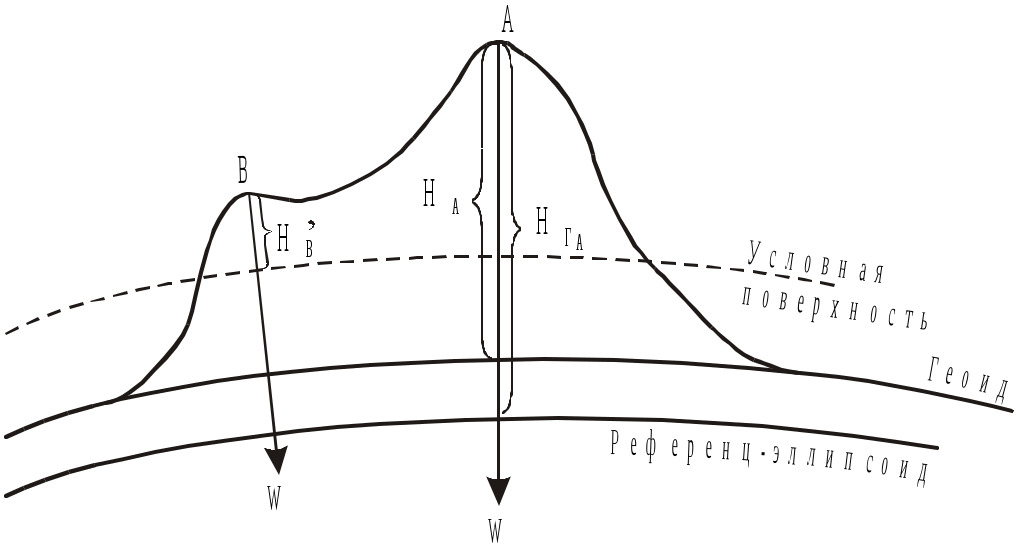 Рис.4. Системы высот Кроме того, следует знать, что горизонтальные поверхности, перпендикулярные вектору силы тяжести, не параллельны между собой (они сжимаются у полюса) и поэтому высоты точек, лежащих на некоторой уровенной поверхности, уменьшаются по мере приближения к полюсу. Это уменьшение выражается формулой  ,где  разность широт точек, выраженная в радианной мере.Например, воды озера Байкал, расположенные на средней широте ср=53,5, с размахом широт 4,3 и средней высотой H=450 м на севере и юге отличаются по высоте на 0,2 м. Превышением называется разность высот двух точек. На небольшой территории (в несколько десятков квадратных километров) величина h не зависит от принятой системы высот, получается, что  . Понятие о равноугольной проекции Гаусса-Крюгера и общегосударственной системе плоских прямоугольных координат Самостоятельное изучение. Литература: Лекции по инженерной геодезии (с фрагментами методического комплекса). Учебное пособие/ В.П. Абрамов; под редакцией О.С. Разумова. – Тула, 2005. С 8–9. Лекция 2. Ориентирование линий. Прямая и обратная геодезические задачи Ориентировать линию местности – значит определять ее направление относительно некоторого другого направления, принятого за исходное. В геодезии в качестве исходного принимаются направления: 1) истинного меридиана; 2) магнитного меридиана; 3) оси абсцисс или линии, ей параллельной. В этой связи различают три вида ориентирных углов для одной и той же линии. А 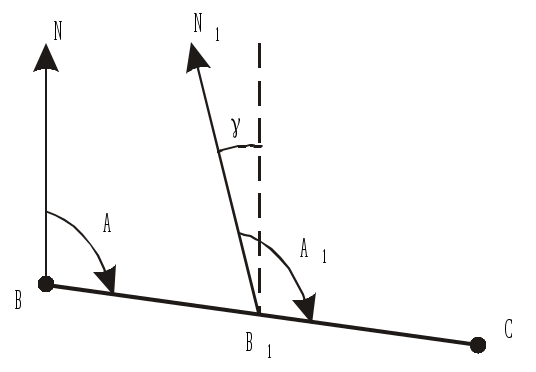 строномический (истинный) азимут – горизонтальный угол А, отсчитанный в начальной точке линии по ходу часовой стрелки от северного направления истинного меридиана этой точки до заданного направления линии (рис.1.10). Угол А может принимать значения от 0 до 360. А Рис.1.10. Истинный азимут зимут линии в разных ее точках меняется на угол между направлением меридианов в этих точках. Этот угол называют сближением меридианов и, как следует из рис.1.10, А1=А+. Истинный азимут может быть определен на местности из астрономических наблюдений или при помощи гироскопического теодолита. Для каждой линии принято различать прямые и обратные направления. Они отличаются друг от друга на 180 и угол сближения меридианов, то есть  . (12)Сам угол равен  , (13)где – разность долгот точек; – средняя широта. Магнитный азимут – горизонтальный угол Am, отсчитанный в начальной точке линии от северного направления магнитного меридиана (магнитной стрелки) по направлению движения часовой стрелки до направления заданной линии.Am может быть измерен на местности с помощью буссоли (компаса). Д 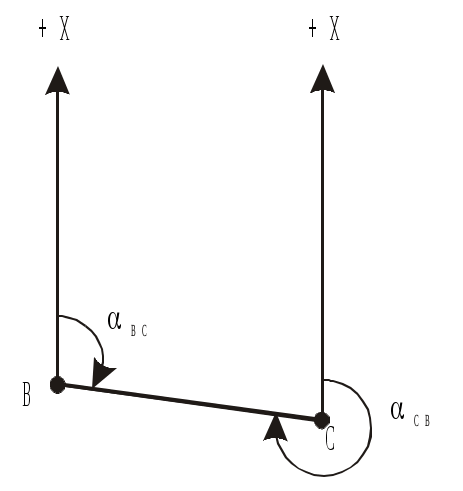 ирекционный угол отсчитывается от положительного направления оси абсцисс или линии, ей параллельной, по ходу часовой стрелки до заданного направления (рис.1.11). Прямой и обратный дирекционные углы отличаются друг от друга на 180, то есть . (14)О Рис.1.11. Прямой и обратный дирекционные углы риентирные углы связаны друг с другом определенными соотношениями. Так, отклонение северного конца магнитной стрелки от направления истинного меридиана называется склонением магнитной стрелки. Эта величина зависит от состояния магнитного поля Земли, которое непостоянно во времени. В районах магнитных аномалий значение может изменяться в значительных пределах и ориентирование по магнитному азимуту там ненадежно. Условно принято считать восточное склонение положительным, а западное отрицательным. На рис.1.12 показано восточное склонение +, и в общем случае связь между истинным и магнитным азимутом выражается формулой  , (15)(в формулу (15) входит со своим знаком). Угол , на который отклоняется в данной точке линия, параллельная оси абсцисс, от направления истинного меридиана, называется Гауссовым сближением меридианов. Как было сказано выше, в проекции Гаусса–Крюгера за ось абсцисс принимается осевой меридиан зоны, поэтому для точки с известными географическими координатами и Гауссово сближение меридианов может быть вычислено по формуле  , (16)где N – долгота осевого меридиана зоны (10). Т Рис.1.12. Связь между ориентирными углами 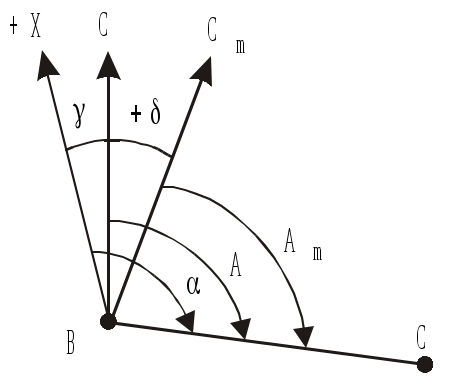 аким образом, для точек, лежащих к востоку от осевого меридиана, сближение меридиана положительное, а западное сближение отрицательное. На осевом меридиане и экваторе =0. Связь между истинным азимутом А и дирекционным углом выражается соотношением  (17)(формула имеет алгебраический смысл). Н 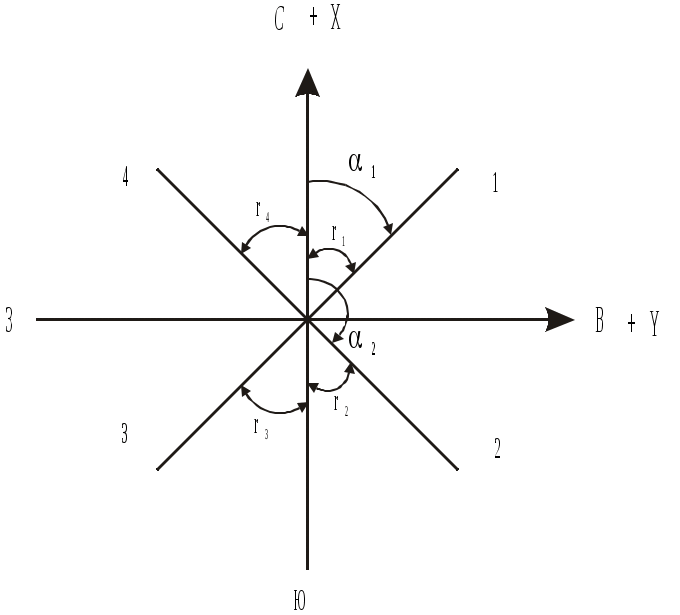 а топографических картах под южной рамкой обычно указывается среднее значение склонения магнитной стрелки и Гауссова сближения меридианов.Д Рис.1.13. Румбы ля ориентирования линий используют еще один ориентирный угол – румб (рис.1.13). Это острый горизонтальный угол rмежду ближайшим концом меридиана (или оси абсцисс) и направлением данной линии. Перед численным значением румба указывают его направление относительно сторон света. Связь между азимутами (дирекционными углами) и румбами показана в табл.1.1. Таблица 1.1 Связь между румбами и дирекционными углами
Прямая геодезическая задача состоит в вычислении координат точки 2 при известных координатах точки 1, расстоянию S12 и дирекционному углу линии 1-2 (рис.1.14). Из треугольника 1С2 следует:  ,  , где х12 и х12 – приращения координат. Поэтому 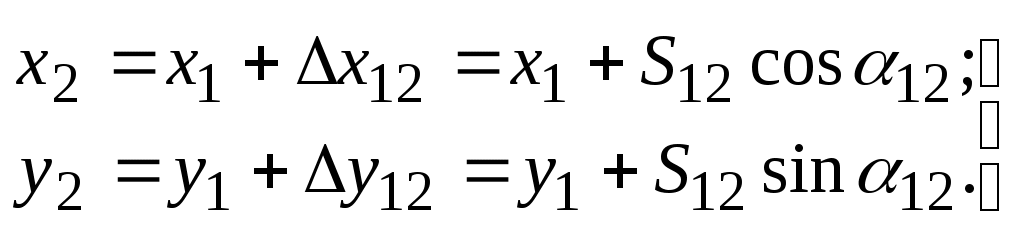 (18)З 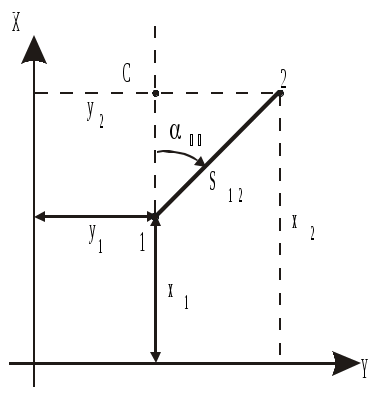 наки у приращений координат определяются знаками тригонометрических функций cos и sin.Обратная геодезическая задача заключается в определении длины линии Sи ее дирекционного угла по координатам концов этой линии, то есть в задаче дано x1, y1, x2, y2. Требуется вычислить 12 и S12. Из треугольника 1С2 (см. рис.1.14) следует, что  Рис.1.14. Прямая геодезическая задача , (19)  . (20)При решении этой задачи на калькуляторе по команде arctg на табло высвечивается значение румба данной линии в градусах и долях градуса. В соответствии со знаками приращений координат (знаки cos и sin) нужно по табл.1.2 определить номер четверти, в которой проходит линия, и от румба перейти к дирекционному углу (см. табл.1.1), выразив его в градусах, минутах и секундах дуги. Таблица 1.2
Изображение рельефа на планах и картах Рельефом называют совокупность неровностей местности естественного происхождения. На топографических картах рельеф обозначают с помощью горизонталей. Горизонталь – это непрерывная кривая линия, соединяющая точки местности, лежащие на одной высоте. Каждую горизонталь можно представить как след сечения рельефа местности уровенной поверхностью. Обычно такие сечения выполняют через определенный интервал по высоте h, который называется высотой сечения рельефа. Высоты горизонталей H отсчитывают от исходной (нулевой) уровенной поверхности, и они везде кратны h. Расстояние между горизонталями в плане называют заложением a, оно на плане уменьшается по мере увеличения крутизны склона. Р 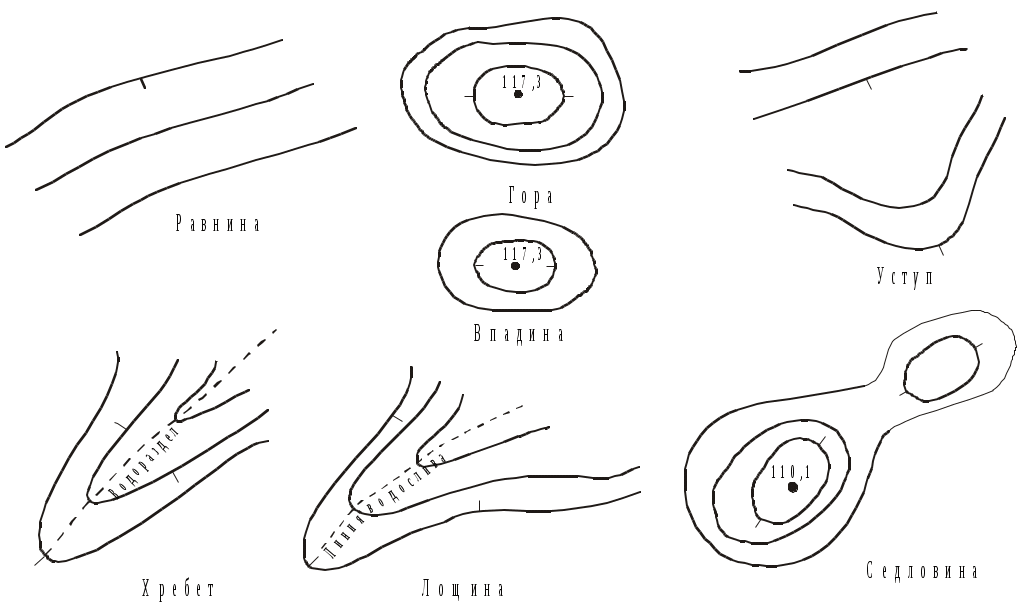 азличают следующие формы рельефа: равнина, гора (холм), впадина (котловина), хребет, лощина, седловина, уступ (терраса) (рис.1.15). О Рис.1.15. Основные формы рельефа Рис.1.16. Условные знаки рельефа 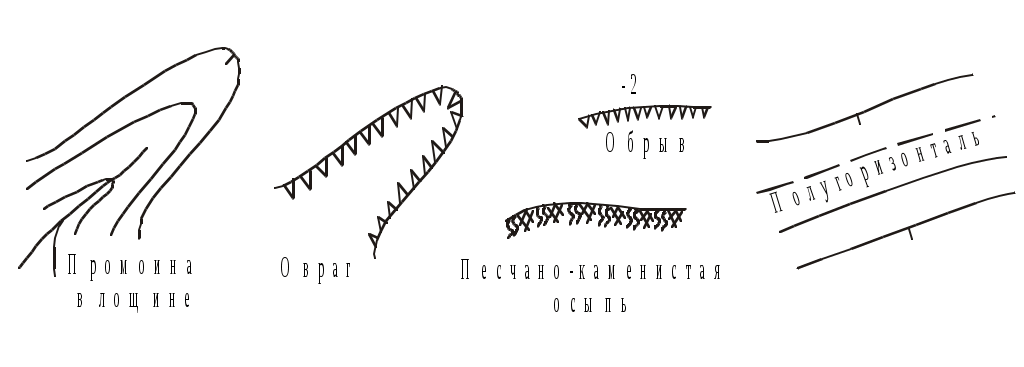 севая линия, соединяющая самые высокие точки хребта, называется линией водораздела. А осевая линия лощины, по которой стекает вода, называется тальвегом (линией водослива). На горизонталях ставят бергштрихи по направлению падения склона. Свойства горизонталей: 1. Они соединяют точки местности, лежащие на одной высоте. 2. Они не пересекаются и не раздваиваются. 3. Их высоты всегда кратны высоте сечения рельефа h. 4. При заданной высоте сечения hрасстояния между горизонталями уменьшаются по мере увеличения крутизны склона. 5. Линии водораздела и водослива горизонтали пересекают под прямым углом. Недостатки горизонталей: 1. Они не обладают наглядностью при изображении рельефа. 2. С их помощью нельзя изобразить любую форму рельефа (идеальную равнину, крутые и нависающие склоны, обрывы и др.). 3. При заданной высоте сечения рельефа его мелкие формы (меньше высоты h) не фиксируются на планах. С учетом этих особенностей при изображении оврагов, промоин или обрывов используют специальные условные знаки (рис.1.16), а для картирования слабо выраженного рельефа проводят дополнительные прерывистые горизонтали через половину или четверть высоты сечения (полугоризонтали или четвертьгоризонтали).  Рис.1.17. Определение высот горизонталей Для определения высоты Н горизонтали по отметке ближайшей к ней точки нужно знать высоту h сечения рельефа. Предположим, что на рис.1.17 h=5 м. На этом рисунке вершина горы расположена на высоте 117,3 м. Отметка ближайшей к ней горизонтали будет равна H=115 м, так как это число кратно высоте сечения и является ближайшим числом, меньшим отметки вершины 117,3 м. В котловине ближайшая к точке дна горизонталь имеет отметку 120 м это число кратно пяти метрам и больше отметки дна. На ровном склоне верхняя горизонталь имеет отметку 125 м, нижняя – 120 м. Если же одна из горизонталей снабжена отметкой (само число пишется так, чтобы верх цифры был обращен к вершине), то отметки соседних горизонталей можно определить, сообразуясь с высотой сечения рельефа и направлением бергштрихов. На рис.1.18 при h=2 м H1=122 м, H2=124 м, H3=126 м. Н Рис.1.18. Определение высоты точки  аконец, чтобы определить отметки точек, лежащих между горизонталями, поступают следующим образом. Сначала находят высоты горизонталей, между которыми расположена точка (А на рис.1.18). Затем через эту точку проводят линию cbнаибольшей крутизны как кратчайшее расстояние между горизонталями. Предполагая, что на протяжении этой лини отметка изменяется на высоту сечения рельефа h равномерно, оценивают на глаз превышение h данной точки над горизонталью Н1 и прибавляют его к отметке этой горизонтали. На рис.1.18 h=0,8 м и НА=122+0,8=122,8 м. Для более точного определения отметки нужно измерить на карте отрезки Ас и bc, тогда  .Крутизну склонов, изображенных на карте, выражают либо углом наклона линии склона к горизонту , либо уклоном i – тангенсом угла наклона этой линии:  , (21)где НАи НВ высоты конечных точек линии склона, dАВ горизонтальное расстояние между точками. Уклоны обычно выражают в сотых долях (процентах, %) от линии склона или тысячных долях (промиллях, ‰). Например, если tg=0,025, то это составляет для уклона i=2,5% =25‰. Для нахождения крутизны склона между соседними разноименными горизонталями измеряют заложение a, то есть расстояние по линии склона между этими горизонталями и, зная h, находят уклон  . (22)Для облегчения решения этой задачи под южной рамкой топографической карты построен график заложений, отражающий изменение заложения a от крутизны склона (при постоянном значении высоты сечения h). Так как согласно (22)  , то для каждого заданного угла наклона было вычислено соответствующее заложение a и построен график в масштабе карты (рис.1.19). Для определения крутизны склона на заданном участке берут в раствор измерителя расстояние между соседними разноименными горизонталями и переносят его на график. На рис.1.19 =2,8. 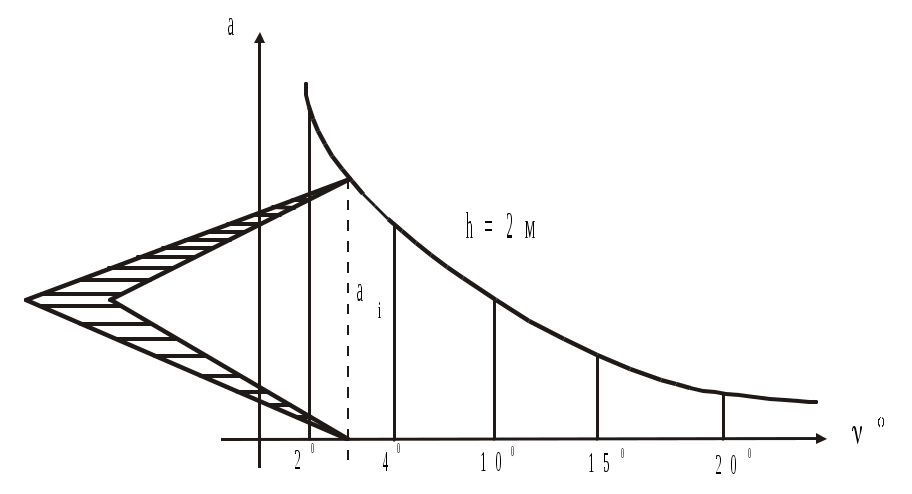 Рис. 1.19. График заложений Номенклатура топографических карт России Все топографические карты многолистные. Каждый лист карты представляет собой трапецию, ограниченную меридианами и параллелями. Номенклатурой называется система обозначений листов многолистных карт. В основу такой системы обозначений положен лист карты масштаба 1:1000000, имеющий протяженность в угловой мере по широте 4 и по долготе 6. Чтобы получить такой лист, земной шар делится на четырехградусные широтные пояса, которые идут от экватора к северу и обозначаются заглавными буквами латинского алфавита, и на шестиградусные колонны по долготе, счет которых ведется от меридиана 180 на восток. Номер колонны отличается от номера координатной зоны на 30 единиц (рис.1.20). Номенклатура листа карты масштаба 1:1000000 состоит из заглавной буквы латинского алфавита, обозначающей широтный пояс, и номера колонны. Например, Москва располагается на листе карты N-37 (рис.1.20). Для определения номенклатуры такой карты для заданного района необходимо по мелкомасштабной географической карте найти приближенные координаты 0, 0 центра этого района. Затем, поделив широту центра 0 на 4, а долготу 0 на 6, получим числа, целые части которых показывают номера “a” пояса и (“b”+30) колонны, граничащих с юга и запада с искомой трапецией. Например, для Москвы 0=55,3, 0=36,8. Поэтому 0:4=13,8 (a=13) и 0:6=6,8 (b=6). Номер искомого широтного пояса, где расположена наша точка, будет на единицу больше, то есть a+1=14. Это соответствует четырнадцатой букве N латинского алфавита. А номер искомой меридианальной колонны будет соответственно равен b+1+30=37. Таким образом, номенклатура миллионного листа карты для Москвы составит N-37. Лист карты ограничен с юга и севера параллелями 52 и 56, а с запада и востока – меридианами 36 и 42. Карты масштаба 1:500000 образуются делением миллионного листа на четыре части протяженностью 2 по широте и 3 по долготе. Каждая такая трапеция обозначается заглавными буквами русского алфавита А, Б, В и Г и содержит номенклатуру миллионного листа, в котором они расположены. Например, Москва расположена на листе N-37-А. Карты масштаба 1:100000 образуются делением миллионного листа на 144 части (по 12 частей по широте и долготе). Полученные таким образом трапеции несут номера от 1 до 144 вместе с номенклатурой миллионного листа. Например, центр Москвы расположен на листе N-37-26 (см. рис.1.21). Размер трапеций карт масштаба 1:100000 20 по широте и 30 по долготе. Н Рис.1.21. Номенклатура топографических карт России 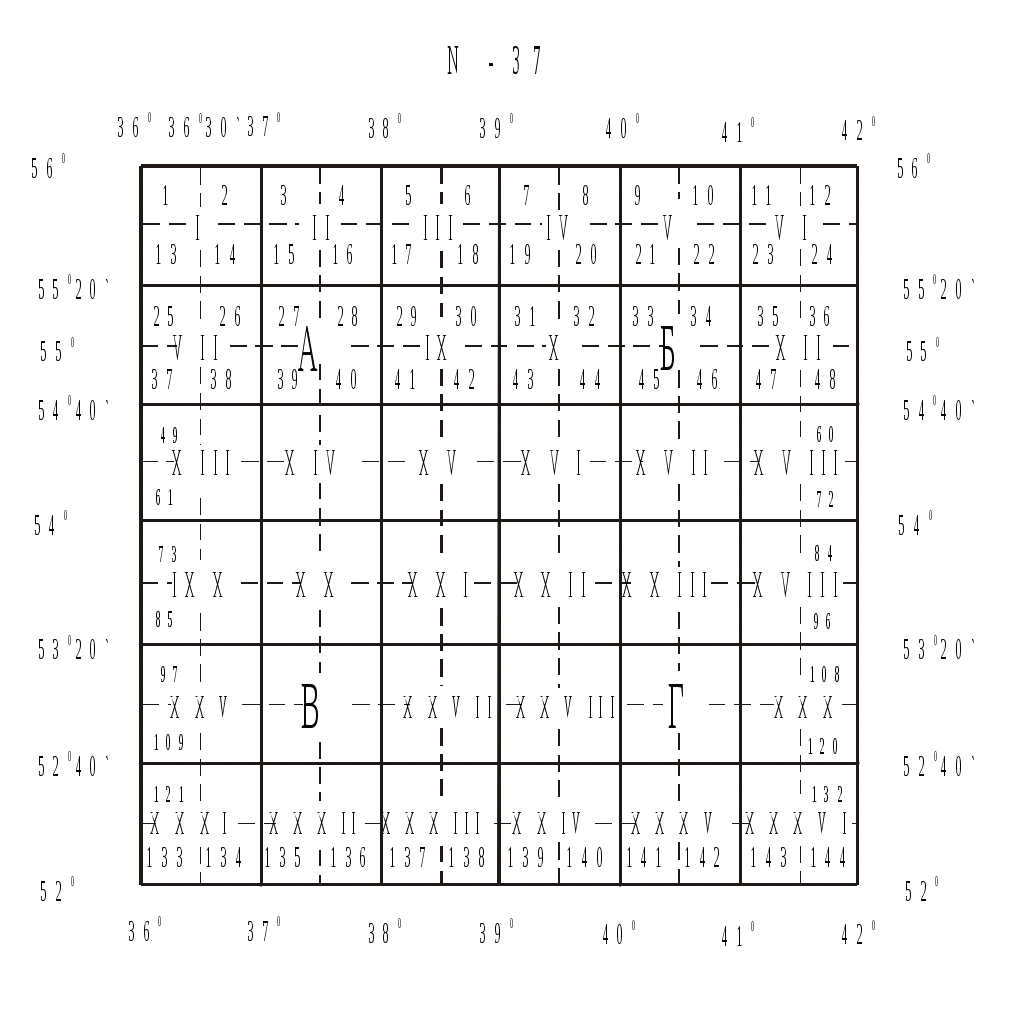 оменклатура карт более крупных масштабов несет в себе номенклатуру стотысячных листов, которые последовательно делятся на более мелкие части. Так, карта масштаба 1:50000 образуется делением стотысячного листа на четыре части, каждая из которых обозначается заглавными буквами русского алфавита. Протяженность таких трапеций по широте составляет 10, а по долготе 15 (рис.1.22). Н 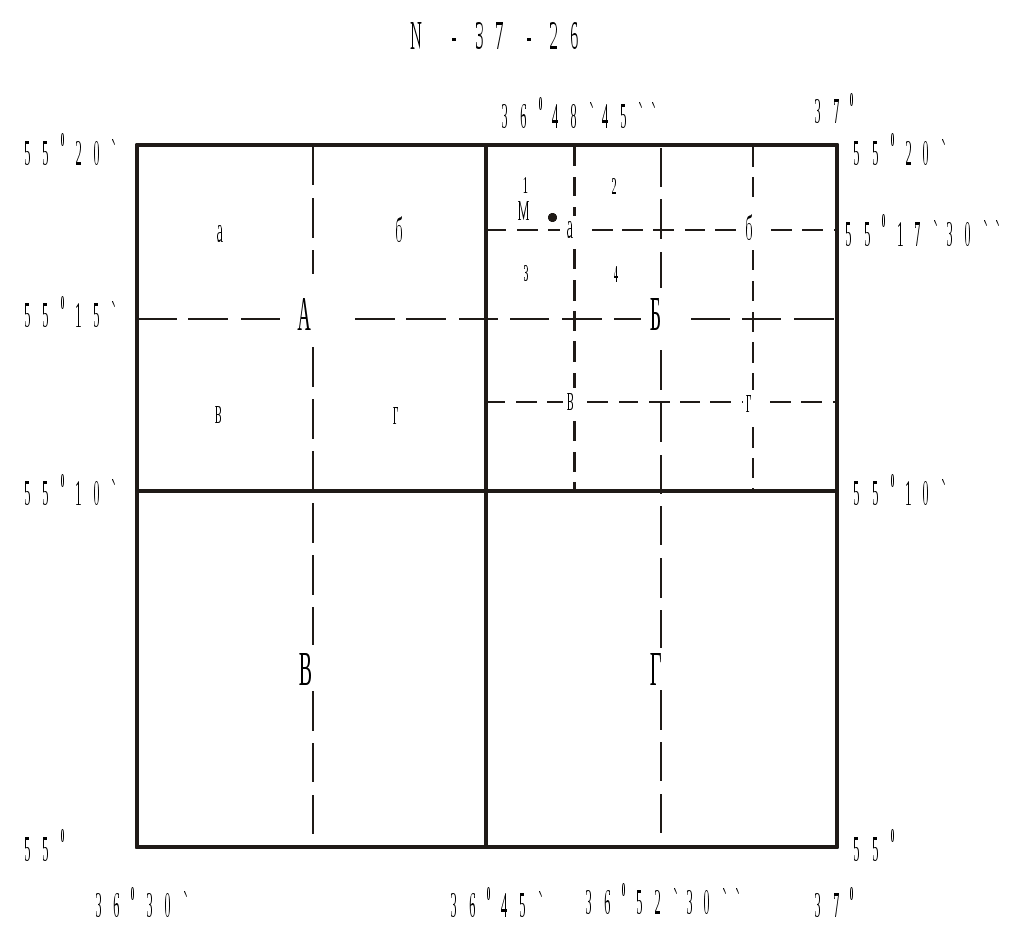 оменклатура такого листа состоит из номенклатуры стотысячного листа и индекса трапеции А, Б, В, Г. Для центра Москвы номенклатура составит N-37-26-Б. Ч Рис.1.22. Разграфка карт масштаба 1:50000 – 1:10000 тобы получить карту масштаба 1:25000, нужно пятидесятитысячную карту поделить на четыре части и обозначить их строчными буквами русского алфавита вместе с номенклатурой пятидесятитысячного листа, то есть N-37-26-Б-а. Наконец, для масштаба 1:10000 карта масштаба 1:25000 делится на 4 части (1, 2, 3, 4) и обозначается в виде N-37-26-Б-а-1 (для центра Москвы). В табл.1.3 показана номенклатура карт стандартных масштабов. Номенклатура планов более крупных масштабов чаще всего носит условный характер и разрабатывается в отдельных регионах самостоятельно, хотя общегосударственный стандарт предусматривает, что лист карты масштаба 1:100000 служит основой для разграфки листов планов масштабов 1:5000 и 1:2000. Так ,одному листу карты масштаба 1:100000 соответствует 256 (1616) листов карты масштаба 1:5000, которые обозначаются арабскими цифрами 1-256, записываемыми в скобках. Для последнего листа масштаба 1:5000, находящегося в пределах площади N-37-26, номенклатура будет N-37-26-(256). Протяженность этого листа по широте составит 115, а по долготе 152,5. Таблица 1.3 Номенклатура топографических карт
Для получения листа плана 1:2000 лист масштаба 1:5000 делят на девять частей (33) и обозначают строчными буквами русского алфавита а, б, в, …, и, также заключаемыми в скобки. Тогда последний лист масштаба 1:2000 рассматриваемого района будет иметь номенклатуру N-37-26-(256-и). Он будет иметь протяженность по широте 25 и по долготе 37,5. На небольших территориях (до 20 км2) для топографических планов масштаба 1:5000 1:500 допускается прямоугольная разграфка с размером листов 4040 см (22 км) для масштаба 1:5000 и 5050 см для масштабов 1:2000, 1:1000, 1:500. В этом случае за основу разграфки принимается лист масштаба 1:5000 с соответствующим номером. Он делится на четыре листа масштаба 1:2000, каждый из которых обозначается прописными буквами русского алфавита (А, Б, В, Г), например,(5-Г). В свою очередь, листу плана масштаба 1:2000 соответствуют четыре листа масштаба 1:1000, обозначаемые римскими цифрами (I, II, III, IV), например, (5-Г-III) и 16 листов (44) масштаба 1:500, обозначаемые арабскими цифрами (5-Г-15) и т.д. Общие характеристики топографических карт При работе с топографическими картами вначале необходимо познакомиться с ее техническими характеристиками, к которым относятся: - номенклатура карты; - масштаб (численный и именованный), точность масштаба; - географические границы листа карты; - номер координатной зоны; - интервал сетки прямоугольных координат; - высота сечения рельефа; - средние значения магнитного склонения и сближения меридианов. Номенклатура карты обычно подписывается над северной рамкой карты с указанием наиболее крупного населенного пункта. Номенклатура соседних листов подписывается посередине внешней рамки карты. Численный масштаб подписывается под южной рамкой карты. Он представляет собой дробь 1/M, в числителе которой единица, а знаменатель М указывает на степень уменьшения линий на карте по сравнению с горизонтальными проекциями тех же линий на местности, то есть  , (23)где Sк – расстояние по карте; Sм расстояние на местности. Используя соотношение (23), можно решить ряд задач, связанных с масштабами. Вместе с численным масштабом карты дается его расшифровка в виде именованного масштаба, который указывает, сколько метров на местности содержится в 1 см карты. Например, если масштаб карты 1:5000, то есть 1 см карты соответствует 5000 см на местности, то именованный масштаб указывает, что в 1 см 50 м. Точностью масштаба карты называют наименьший отрезок на местности, который можно изобразить и различить на карте соответствующего масштаба. Поскольку наименьший отрезок, различимый простым глазом, равен 0,01 см=0,1 мм, то согласно формуле (23), соответствующее ему расстояние на местности равно St=0,01смМ – это и будет точностью масштаба карты. Например, при масштабе 1:5000 точность масштаба St=0,01см5000=50см. Если же поставить обратную задачу и заказать такую карту, на которой бы четко различались наименьшие детали, равные St, то масштаб такой карты должен быть  . (24)Например, если задать St=1м, то карта должна быть составлена в масштабе  .Рис.1.23. Определение по карте координат, дирекционных углов и азимутов 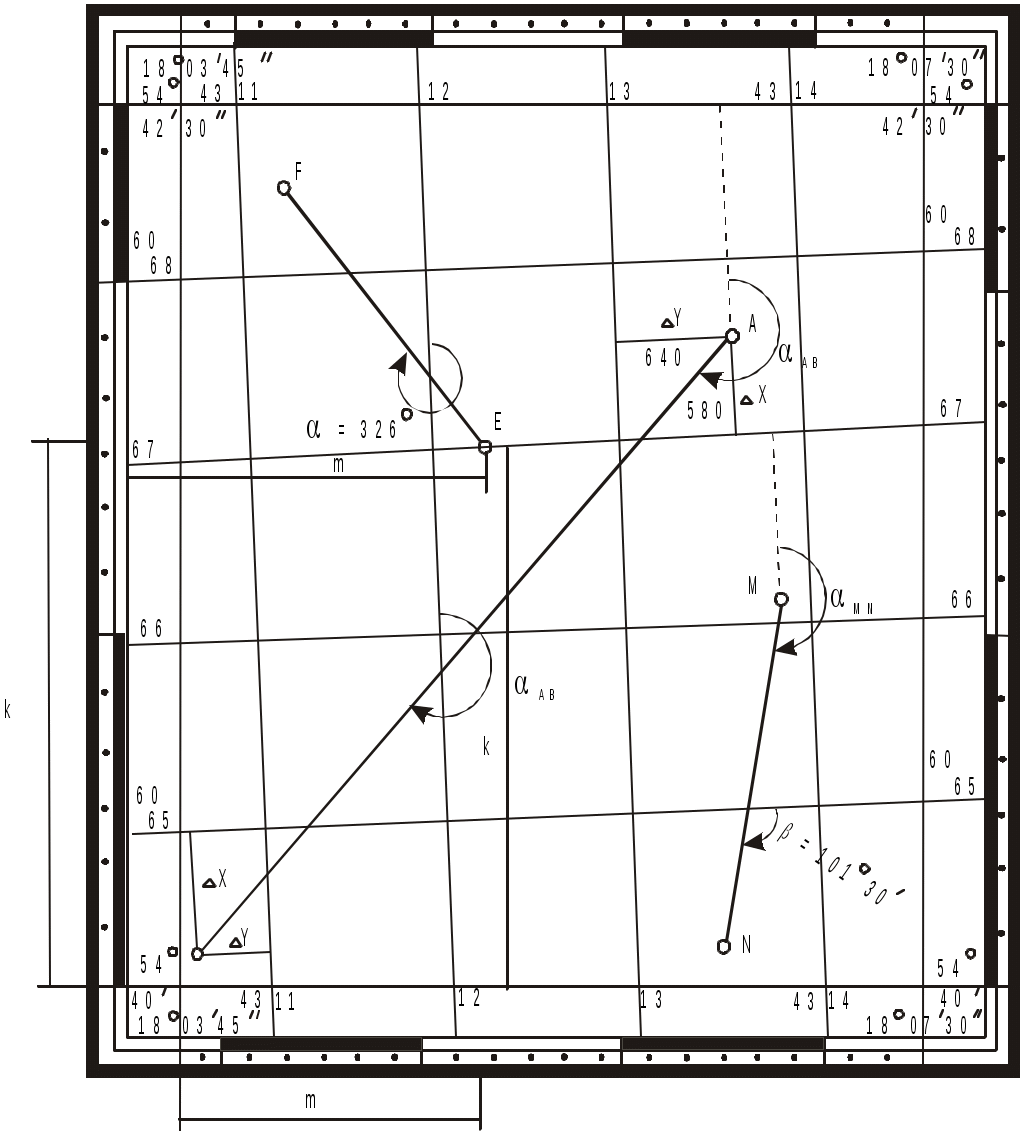 На некоторых картах дополнительно дается изображение линейного масштаба, который представляет собой прямую линию, разделенную на равные отрезки (равные 1 см или 2 см), которые называют основанием масштаба, и против каждого деления основания подписывается соответствующее ему расстояние на местности. Крайнее левое основание делится на 10 частей. С помощью такого построения можно уверенно измерять или откладывать на карте отрезки с точностью до десятых долей основания. Географическими границами листа карты запада и востока служат линии меридианов, а с севера и юга – линии параллелей. Эти линии образуют внутреннюю рамку, которая ограничивает изображение местности на карте (рис.1.23). Географические границы листа определяются широтами и долготами этих меридианов и параллелей, подписанных в углах рамки карты. Параллельно внутренней рамке проведена минутная рамка, разделенная на минуты дуги черными (четными) и белыми (нечетными) интервалами. В свою очередь, минуты разделены точками на десятисекундные интервалы. Минутная рамка используется для определения географических координат точек, нанесенных на карту. Номер координатной зоны, в которой находится данная карта, можно определить по долготе западного меридиана. Если эту долготу разделить на 6˚, то целое число этой дроби указывает на число прошедших зон, а карта будет относиться к следующей зоне. Например, если λ3=64˚ 30΄, то  , и это значит, что до данной карты прошло 10 зон, а наша карта расположена в 11-й зоне. Кроме того, номер зоны равен уменьшенному на 30 номеру меридианальной колонны из номенклатуры. Так, если карта имеет номенклатуру R-38-56, то номер зоны равен 38-30=8. Наконец, номер зоны подписывается перед значением ординат вертикальных линий, подписанных на прямоугольной координатной сетке карты.Интервал сетки прямоугольных координат на картах масштаба 1:10000 1:100000 бывает равным 1 км или 2 км. Целое число километров абсцисс и ординат подписывается за внутренней рамкой карты у горизонтальных и вертикальных линий этой сетки. Высота сечения рельефа подписывается под южной рамкой карты; там же может быть показан график заложений для определения крутизны скатов по расстояниям между горизонталями. Величины магнитного склонения и сближения меридианов указаны у южной рамки карты. Там же дается схематичный чертеж взаимного расположения основных ориентирных линий – истинного и магнитного меридианов и оси абсцисс (см. рис.1.12). Измерение площадей фигур Существуют три способа измерения площадей на картах: графический, аналитический и механический. П Рис.1.29. Определение площади по координатам вершин  ри графическом способеизмеряемый контур разбивается на ряд геометрических фигур, с помощью поперечного масштаба измеряются их элементы и вычисляются площади, которые затем суммируются. Второй вариант графического способа предусматривает использование палетки – сетки квадратов, нанесенной на лист прозрачной бумаги. Зная площадь каждого квадрата в масштабе карты, подсчитывают число полных квадратов, покрывающих заданный контур, а из неполных на глаз составляют полные. Затем все числа складывают. Аналитический способпредназначен для определения площадей многоугольников по координатам их вершин. На рис.1.29 искомую площадь многоугольника P1234 можно представить как функцию площадей прямоугольных трапеций: P1234=P1’122’+P2’233’-P4’433’-P1’144’. Основания каждой трапеции здесь равны абсциссам X точек, а высота – разностям ординат Y. Поэтому 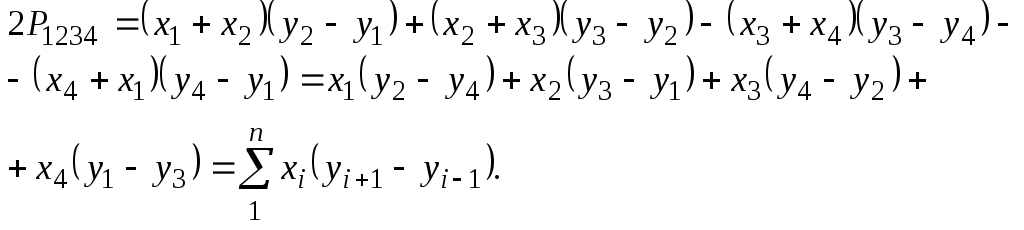 (27)М Рис.1.30. Схема планиметра 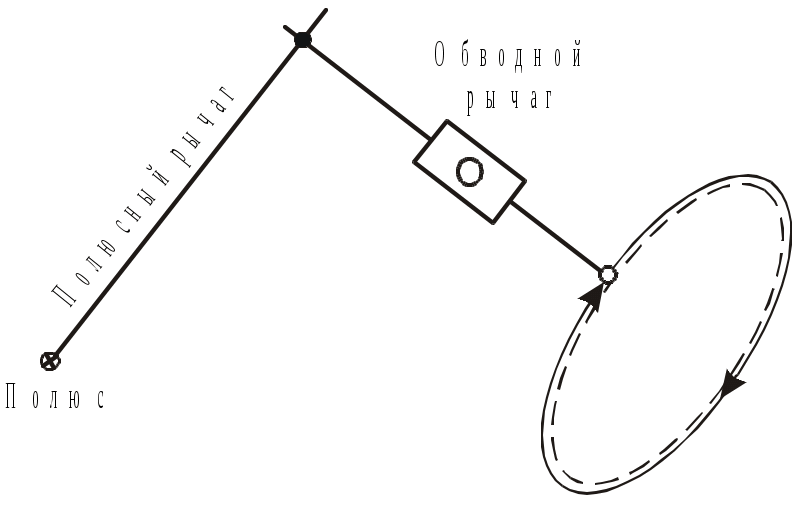 еханический способпредполагает использование специального прибора для измерения площадей – планиметра. Современный полярный планиметр состоит из двух рычагов – полюсного и обводного (рис.1.30, 1.31), которые соединяются шарнирно. На обводном рычаге расположен счетный механизм, а на конце рычага – обводной шпиль или прозрачная марка с точкой, которой обводится контур. Для измерения площади небольших фигур полюс устанавливают вне фигуры с таким расчетом, чтобы при обводе контура углы α между полюсным и обводным рычагами находились в пределах 30˚≤α≤150˚. Для измерения площади до начала обвода марка (обводной шпиль) устанавливается на контур фигуры и снимается начальный отсчет n1. Этот отсчет состоит из числа полных оборотов диска (снимается по циферблату), числа целых делений барабана, прошедших до нуля верньера (две цифры), и долей деления, снимаемых по совпадающему штриху нониуса (верньера). Так, отсчет на рис.1.31 n=6458. После обвода фигуры и возвращения в начальную точку снимается второй отсчет n2. Площадь фигуры в делениях планиметра P=(n2-n1) делений. Если известна цена одного деления планиметра μ (в квадратных метрах или гектарах), то искомая площадь составит  . (28)Для определения цены деления планиметра необходимо измерить этим прибором площадь какой-либо фигуры с известными размерами и площадью P0 (например, один или несколько квадратов координатной сетки). Тогда 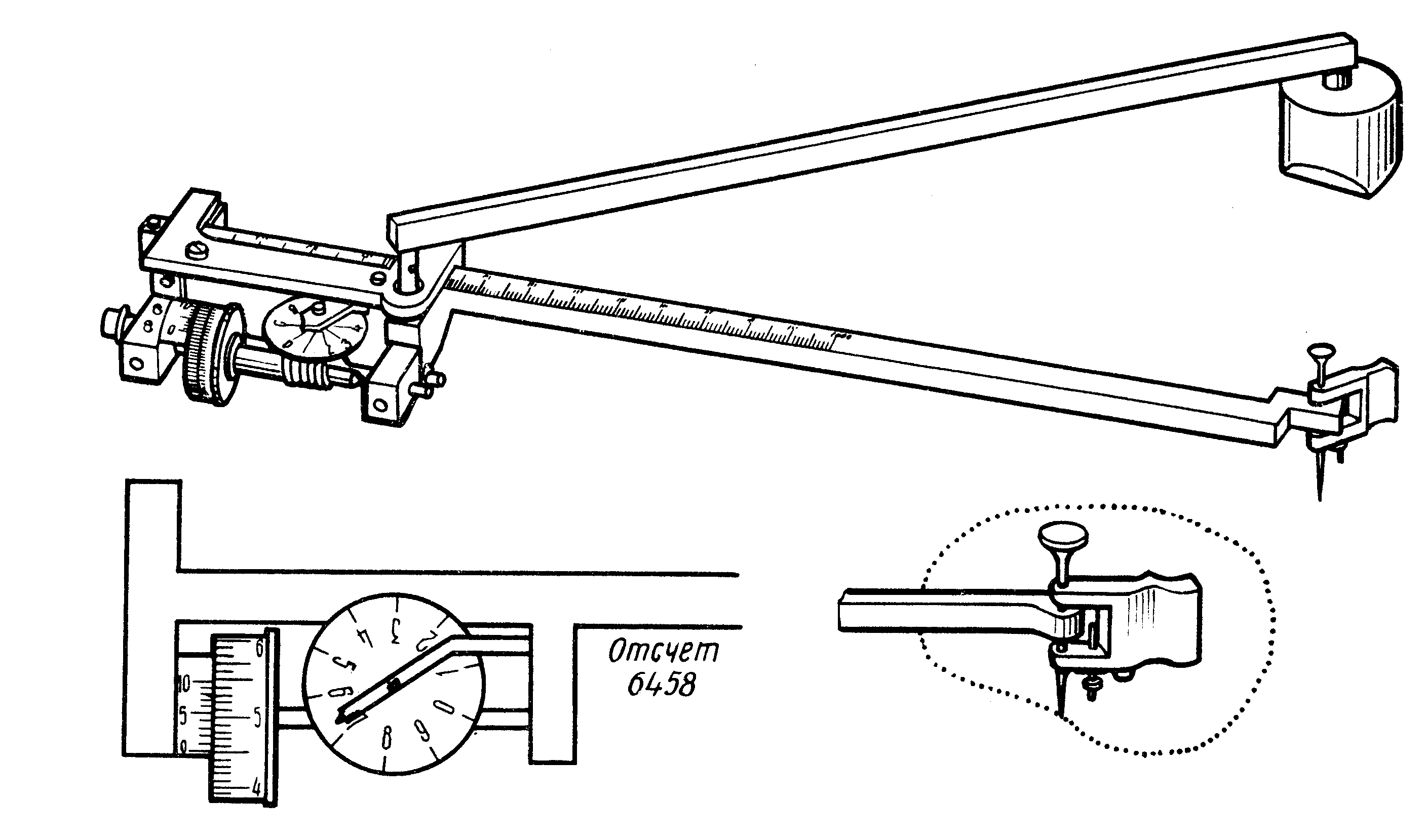 . (29) Рис.1.31. Планиметр В целях контроля и повышения точности площадь фигуры измеряют несколько раз. Если измеряемый участок велик, то полюс планиметра ставят внутри фигуры. Тогда  . (30)Для определения постоянного числа Qнеобходимо и достаточно измерить площадь одного и того же участка с полюсом вне фигуры и внутри фигуры. Если при этом получена разность отчетов  и  , то площадь P равна  , откуда  , (31)где N1 – разность отсчетов при измерениях с полюсом вне фигуры, N2 – разность отсчетов при измерениях с полюсом внутри фигуры. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||