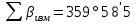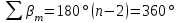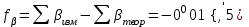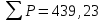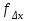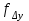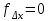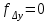Контрольная работа 1. Контрольная работа по учебному курсу Геодезия 1 Вариант 10 (при наличии) Студент
 Скачать 1.08 Mb. Скачать 1.08 Mb.
|
|
М  ИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ ИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИфедеральное государственное бюджетное образовательное учреждение высшего образования «Тольяттинский государственный университет» Архитектурно-строительный институт Центр архитектурных, конструктивных решений и организации строительства КОНТРОЛЬНАЯ РАБОТА по учебному курсу «Геодезия 1» Вариант _10_ (при наличии)
Тольятти 2023 1. Контрольная работа Вопрос 1. Как по топографической карте запроектировать трассу с заданным уклоном – 0,015%? Ответ дополнить схемой. Ответ: У нас имеется топографическая карта масштаба 1:2000 с высотой сечения рельефа 1м и график заложений по уклонам на ней отсутствует, на ней необходимо запроектировать трассу от точки А к точке В. Для решения поставленной задачи определим кратчайшее расстояние на местности между точками на горизонталях, пользуясь формулой: 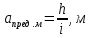 где h – разность высотных отметок точки и меньшей горизонтали или высота сечения рельефа (1м), м; i – уклон. 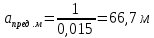 Переведем полученное значение длины на местности в длину линии на плане по формуле: 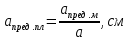 где: 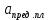 – величина предельного заложения в масштабе плана, см; – величина предельного заложения в масштабе плана, см;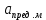 - величина предельного заложения на местности, м; - величина предельного заложения на местности, м;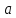 - число метров на местности, соответствующее числу сантиметров на плане, м. - число метров на местности, соответствующее числу сантиметров на плане, м.Масштаб 1:12000 означает, что 1 см на плане соответствует 2000 см на местности, или 20м ( 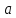 =20). =20).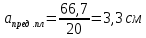 Далее циркулем откладываем расстояние 3,3 см, острием циркуля становимся на точку А и отмечаем на соседней горизонтали штрихами места пересечения (назовем эти точки условно 1 и 1´). Т.к. направление на точку 1´ ведет в противоположную сторону, то дальнейшее проектирование будем производить от точки 1. Далее по такому же принципу движемся в сторону точки В. 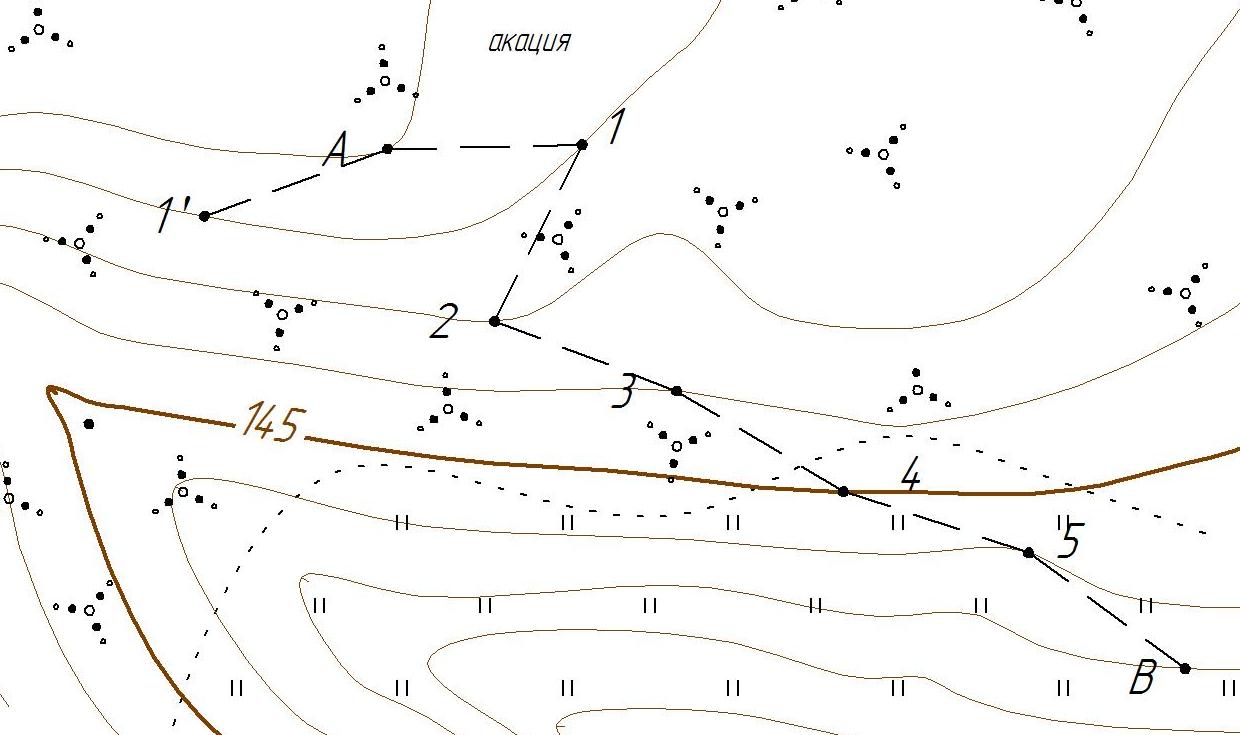 Рис. 1 – Проектирование трассы заданного уклона Вопрос 2. Грубые ошибки (погрешности) геодезических измерений, как их избежать? Ответ: При геодезических измерениях неизбежны ошибки. Эти ошибки бывают грубые, систематические и случайные. К грубым ошибкам относятся просчеты в измерениях по причине невнимательности наблюдателя или неисправности прибора, и они полностью должны быть исключены. Это достигается путем повторного измерения. Грубые погрешности и можно назвать ошибками наблюдателя, поскольку они являются результатом действия человека (допустил промах, не заметил неисправность прибора и т.п.). Результаты грубых измерений обнаруживаются при повторных измерениях, отбраковываются и заменяются новыми. Вопрос 3. Как наносятся по координатам на план вершины теодолитных ходов, и как контролируется правильность их нанесения? Ответ: Точки по их координатам наносят на план при помощи циркуля – измерителя, вычерченного заранее на плотном ватмане графика поперечного масштаба. Предположим, требуется нанести точку с координатами Х2 = +461,13 м, Y2 = 746,88 м. Сначала выясняют, в каком из квадратов сетки должна лежать эта точка: по направлению оси Х точка должна находиться между линиями сетки с абсциссами +400 и +500, по направлению оси Y – между линиями сетки с ординатами +700 и +800 (рис. 2). От линии с абсциссой +400 по вертикальным сторонам этого квадрата откладывают вверх в масштабе расстояние 61,13 м (см. рис. 63) и проводят линию, параллельную оси Y. Вдоль этой линии от вертикальной линии сетки с ординатой +700 откладывают вправо расстояние 46,88 и в масштабе плана. Все построения выполняются с точностью 0,1 мм. Полученную точку накалывают острием ножки циркуля, обводят окружностью диаметром 1,5 мм. Внутри этой окружности никакие линии проводить нельзя. Рядом с кружком подписывают номер точки. 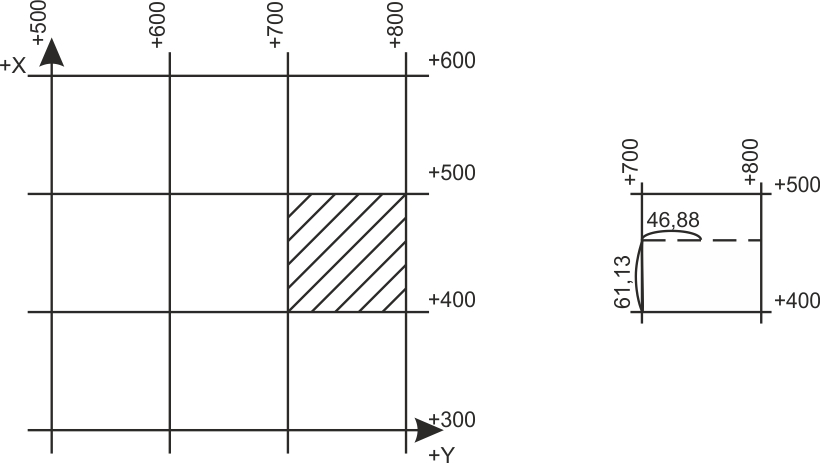 Рис. 2 – Нанесение на план точек теодолитного хода Нанесение точек по координатам контролируется по известному горизонтальному расстоянию между вершинами хода, записанному в ведомости координат. Это расстояние, взятое по поперечному масштабу при помощи циркуля, сравнивается с расстоянием между теми же точками на чертеже. Расхождение допускается не более 0,2 мм. При большем расхождении проверяется правильность нанесения точек по координатам, а при отсутствии погрешностей – правильность построения координатной сетки. После построения вершин теодолитных ходов и контроля работы, их последовательно соединяют тонкими линиями, причем линию доводят до кружка, очерченного вокруг нанесенной по координатам точки. Построенное таким образом плановое обоснование служит опорой для нанесения контуров местности. 2. Контрольная работа «План теодолитной съемки» Исходные данные: - дирекционный угол начальной линии 1-2 α1-2=115°46’; - координаты точки 1 X1=500,00м, Y1=200,00м; - абрис съемки (рисунок 3); - журнал измеренных углов и длин сторон хода (таблица 1). 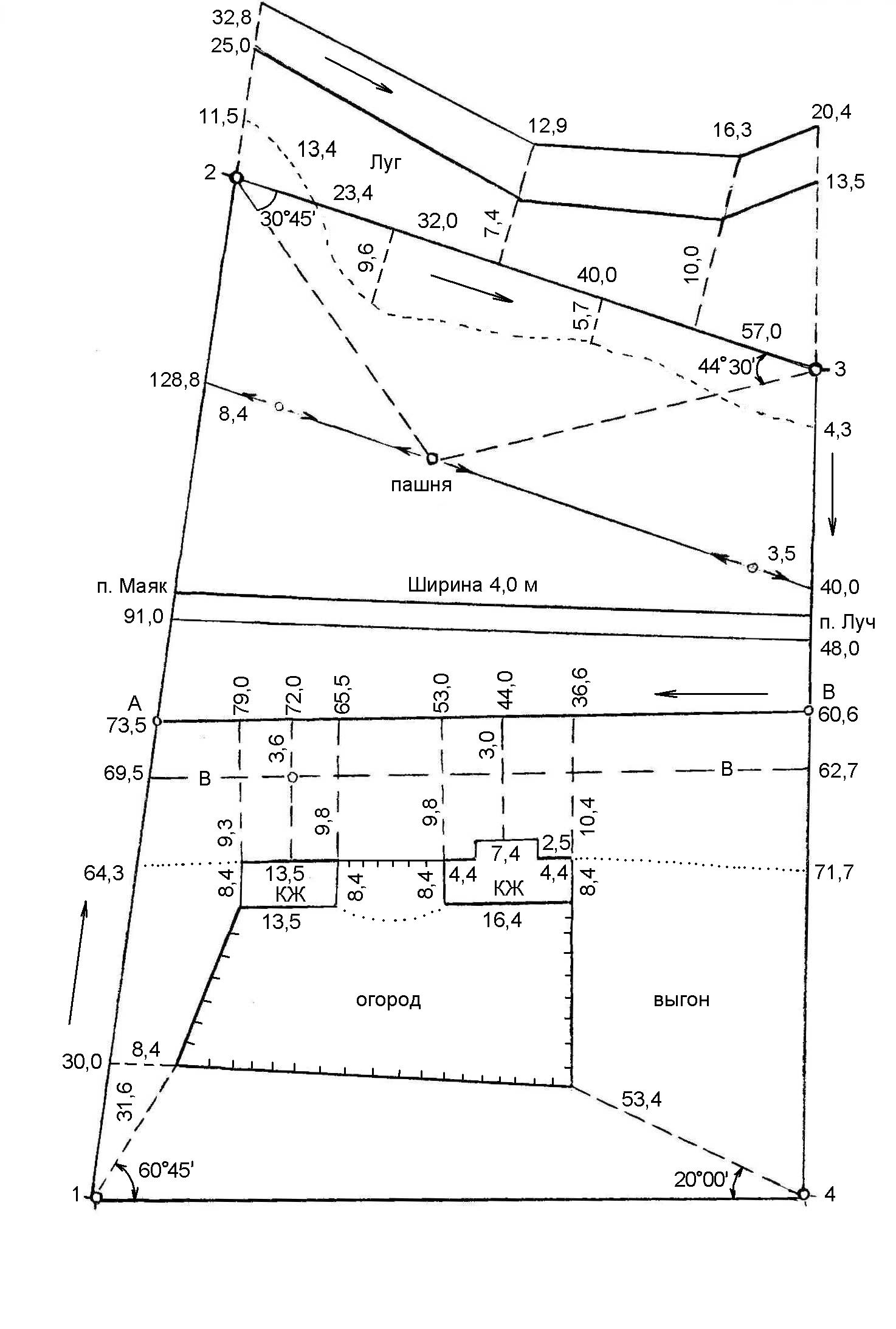 Рисунок 3 – Абрис теодолитной съемки Таблица 1 Журнал измерения горизонтальных углов и сторон теодолитного хода
Увязка углов хода Вычисляем угловую невязку основного замкнутого хода по формуле: 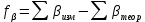 где 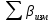 - сумма измеренных углов; - сумма измеренных углов;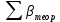 - теоретическая сумма внутренних углов замкнутого теодолитного хода, определяемая по формуле: - теоретическая сумма внутренних углов замкнутого теодолитного хода, определяемая по формуле: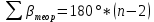 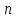 - число углов теодолитного хода. - число углов теодолитного хода. Находим: 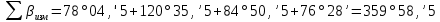 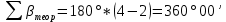 Таким образом 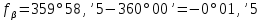 Найденную угловую невязку сравниваем с допустимой невязкой 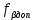 , вычисляемую по формуле: , вычисляемую по формуле: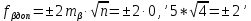 где 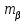 – средняя квадратическая погрешность измерения горизонтального угла одним приемом; – средняя квадратическая погрешность измерения горизонтального угла одним приемом; n – количество измеренных углов. Поскольку угловая невязка допустима, т.е. 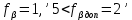 , мы ее распределяем в виде поправки δ с обратным знаком во все измеренные углы. , мы ее распределяем в виде поправки δ с обратным знаком во все измеренные углы.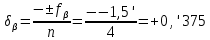 Поскольку полученная невязка не делится на 4 поправки, округленные до 0,1’ без остатка, то мы для удобства вычислений введем поправки в углы, имеющие дробные значения минут, округляя их до целых минут. Вычисляем исправленные углы как угол измеренный плюс поправка по формуле: 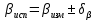 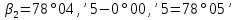 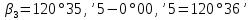 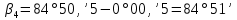 Выполняем проверку увязки углов с помощью равенства: 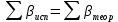 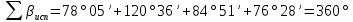 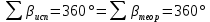 По дирекционному углу исходной стороны и увязанным углам 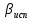 вычисляем дирекционные углы сторон теодолитного хода по формуле: вычисляем дирекционные углы сторон теодолитного хода по формуле: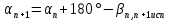 где: 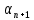 - дирекционный угол последующей стороны; - дирекционный угол последующей стороны;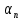 - дирекционный угол предыдущей стороны; - дирекционный угол предыдущей стороны;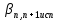 - увязанный, вправо по ходу лежащий угол между предыдущей и последующей сторонами. - увязанный, вправо по ходу лежащий угол между предыдущей и последующей сторонами.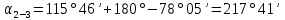 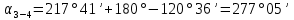 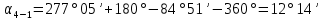 Производим контроль вычислений дирекционных углов. В замкнутом ходе контролем вычислений является получение дирекционного угла начальной стороны 1-2 через дирекционный угол стороны 4-1 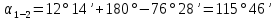 Дирекционные углы сторон переводим в румбы, для более четкого представления о знаках приращений координат, так как по названию румба легко установить знаки приращений координат. Формулы перехода от дирекционных углов в румбы приведены в таблице 2. Таблица 2 Зависимость между дирекционными углами и румбами.
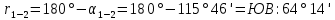 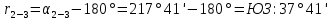 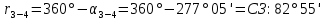 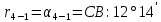 2. Увязка приращений координат ∆ Х и ∆Y 1. Вычисляем приращения координат ∆ Х и ∆Y по вычисленным значениям горизонтальных проложений и румбам: 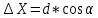 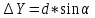 Знаки приращений определяем по названию румба и номеру четверти. 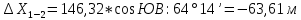 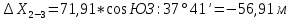 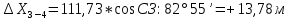 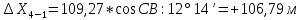 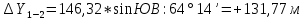 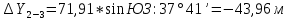 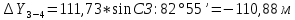 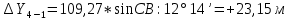 Определяем невязки  и и в приращениях координат по осям X и Y, пользуясь формулами: в приращениях координат по осям X и Y, пользуясь формулами: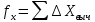 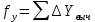 где: 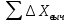 , , 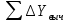 - суммы вычисленных приращений координат. - суммы вычисленных приращений координат.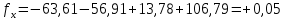 м м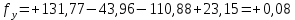 м мНаходим абсолютную линейную невязку в периметре теодолитного хода по формуле: 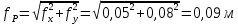 Определяем допустимость невязки 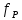 . Для этого вычисляем относительную невязку в периметре как частное от деления невязки в периметре . Для этого вычисляем относительную невязку в периметре как частное от деления невязки в периметре 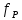 на периметр Р теодолитного хода и сравниваем ее с допустимой относительной невязкой, составляющей на периметр Р теодолитного хода и сравниваем ее с допустимой относительной невязкой, составляющей 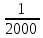 доли периметра. Относительную невязку в периметре представляют в виде дроби, в числителе которой единица. доли периметра. Относительную невязку в периметре представляют в виде дроби, в числителе которой единица.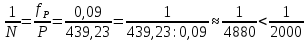 Поскольку относительная невязка допустима, то увязываем вычисленные приращения, вводя в них поправки. Поправки имеют знак, обратный знакам невязок 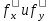 , и распределяются пропорционально длинам сторон по формулам: , и распределяются пропорционально длинам сторон по формулам: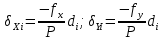 где: 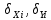 - поправки в приращения координат соответственно по оси Х и Y, найденные для i-й стороны; - поправки в приращения координат соответственно по оси Х и Y, найденные для i-й стороны;Р - периметр полигона; 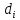 - длина i-й стороны. - длина i-й стороны.Сумма поправок должна равняться невязке с обратным знаком. 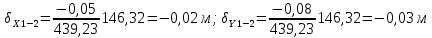 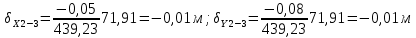 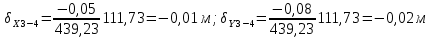 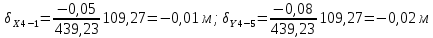 Складывая алгебраически величины вычисленных приращений с их поправками, находим исправленные приращения: 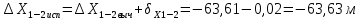 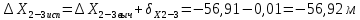 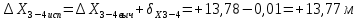 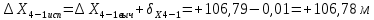 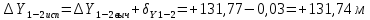 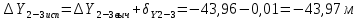 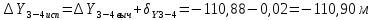 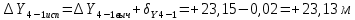 Вычисляем координаты вершин основного замкнутого хода по формулам: 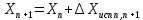 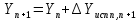 где: 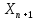 , , 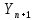 - соответственно абсцисса и ордината последующей вершины теодолитного хода; - соответственно абсцисса и ордината последующей вершины теодолитного хода;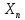 , , 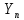 - соответственно абсцисса и ордината предыдущей вершины теодолитного хода; - соответственно абсцисса и ордината предыдущей вершины теодолитного хода;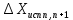 , , 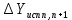 - исправленные приращения координат между предыдущей и последующей вершинами. - исправленные приращения координат между предыдущей и последующей вершинами.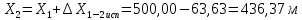 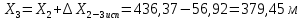 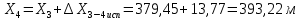 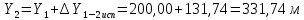 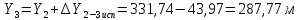 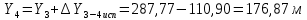 Для контроля вычисляем через координаты точки 5 координаты исходной точки: 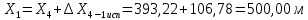 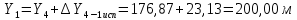 Ведомость вычисления координат замкнутого теодолитного хода
1. Допустимая невязка в углах 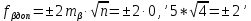 2. Абсолютная невязка в периметре  3. Относительная невязка в периметре 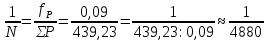 4. Допустимая невязка в периметре 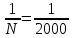 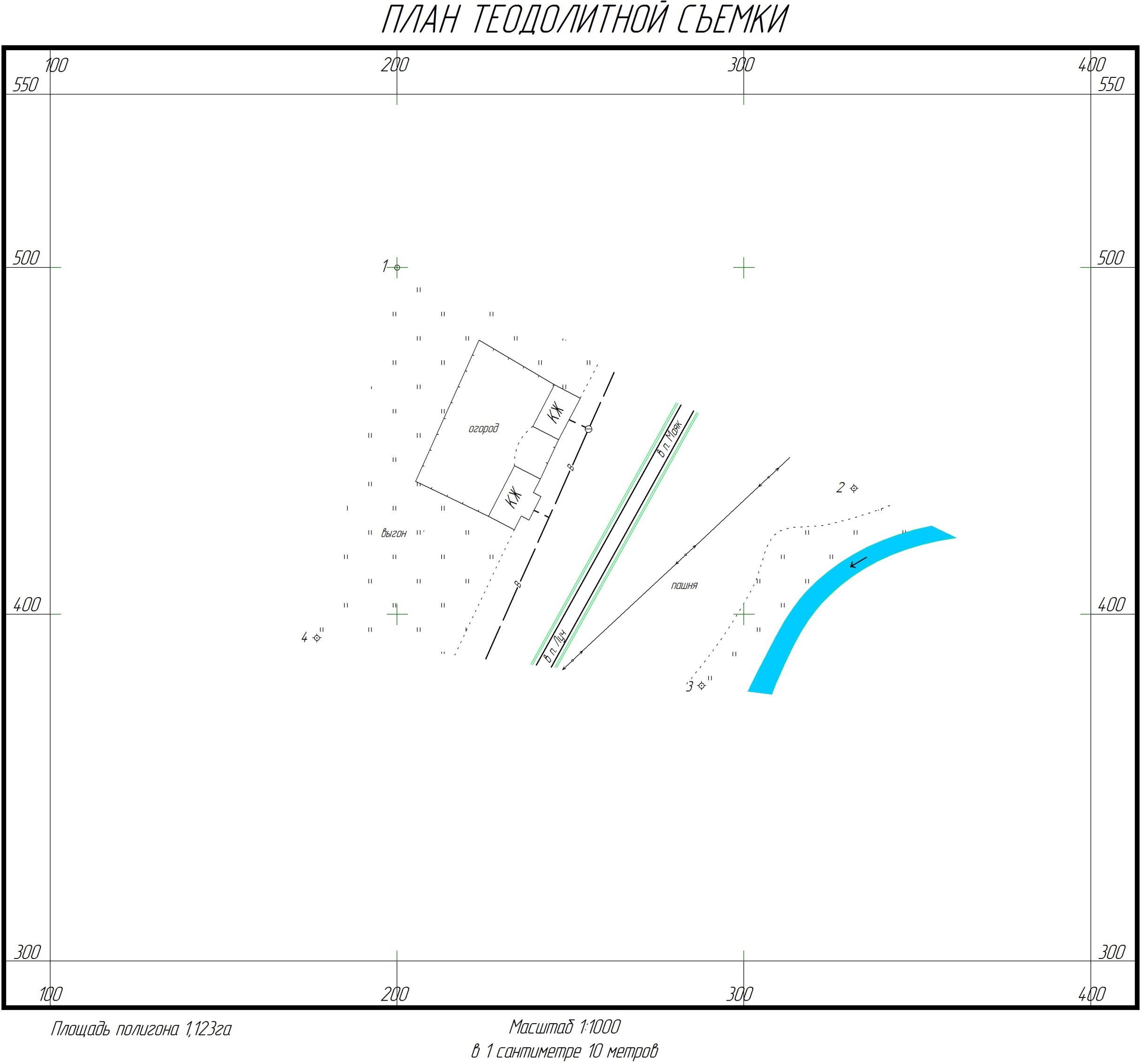 3. Определение площади полигона аналитическим способом Площадь полигона можно вычислить по координатам его вершин. Исходными данными являются координаты станций теодолитного хода (полигона). Двойная площадь полигона (многоугольника) равна сумме произведений абсциссы каждой точки на разность ординат последующей и предыдущей точек: 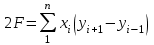 Двойная площадь полигона (многоугольника) равна сумме произведений ординаты каждой точки на разность абсцисс предыдущей и последующей точек теодолитного хода: 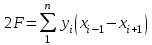 Вычисление площади участка по координатам СХЕМА ПОЛИГОНА 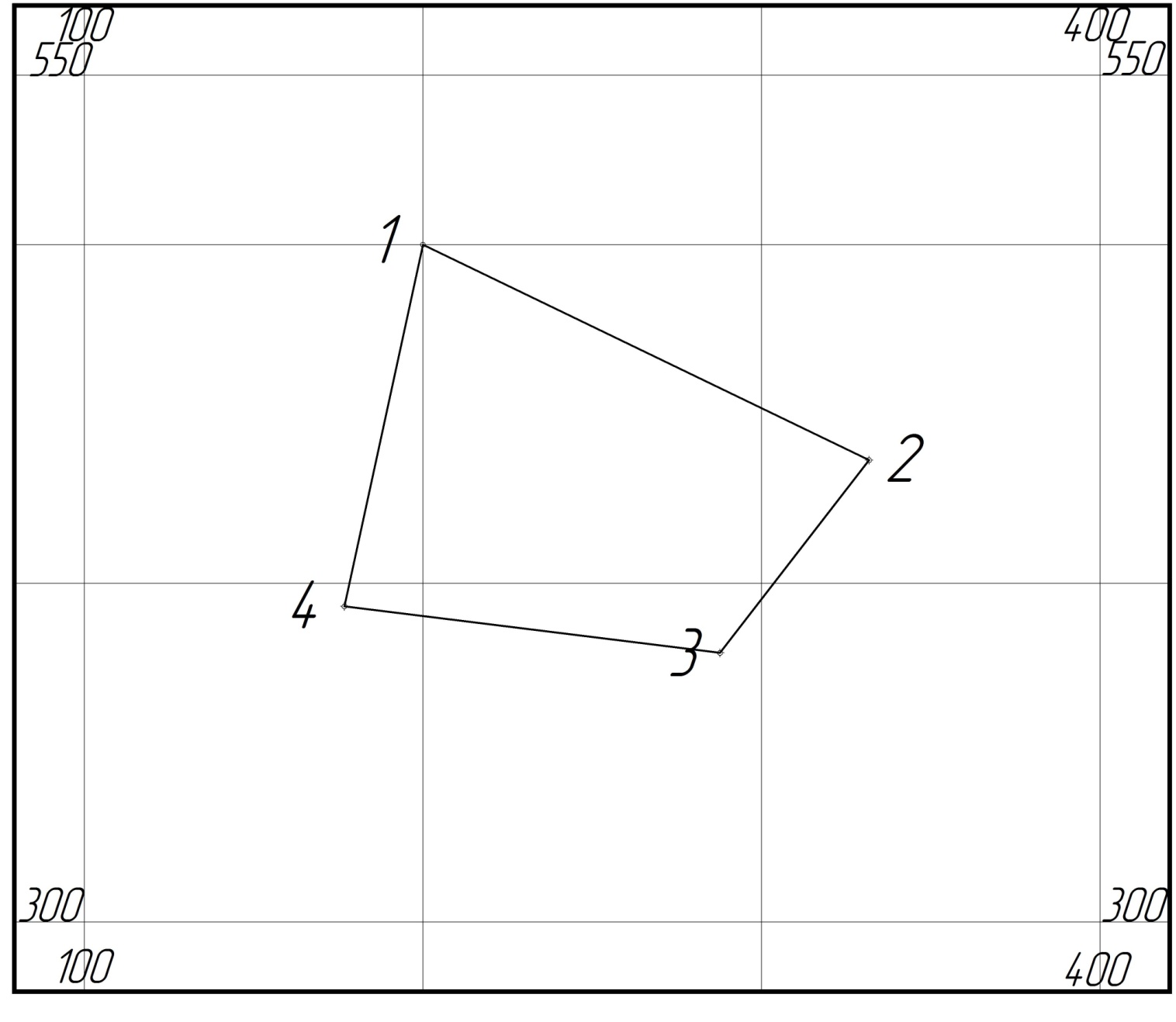 Вычисление площади полигона
Список использованной литературы Инженерная геодезия / Г. В. Багратуни, В. Н. Ганьшин, Б. Б. Данилевич и др. – М.: Недра, 1984. – 344 с. Клюшин, Е.Б. Инженерная геодезия / Е.Б. Клюшин [и др.]. – М.: Academia, 2004. - 479 с. Мальцева Т.Г., Грицкив Л.Н. Учебно-методическое пособие по курсу «Инженерная геодезия» для студентов строительных специальностей и профилей всех форм обучения «Составление плана местности по результатам теодолитной съёмки». – Тольятти: ТГУ, 2010. – 38с. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||