Теодолитный ход. теодолитный ход. Задание вычисление координат точек теодолитного хода
 Скачать 92.33 Kb. Скачать 92.33 Kb.
|
|
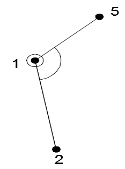
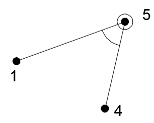
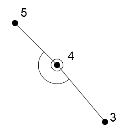
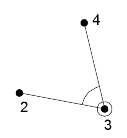
ЗАДАНИЕ «ВЫЧИСЛЕНИЕ КООРДИНАТ ТОЧЕК ТЕОДОЛИТНОГО ХОДА» Задача: познакомиться с теодолитным ходом – способом определения плановых координат; научиться вычислять плановые координаты точек замкнутого теодолитного хода. Схема теодолитного хода 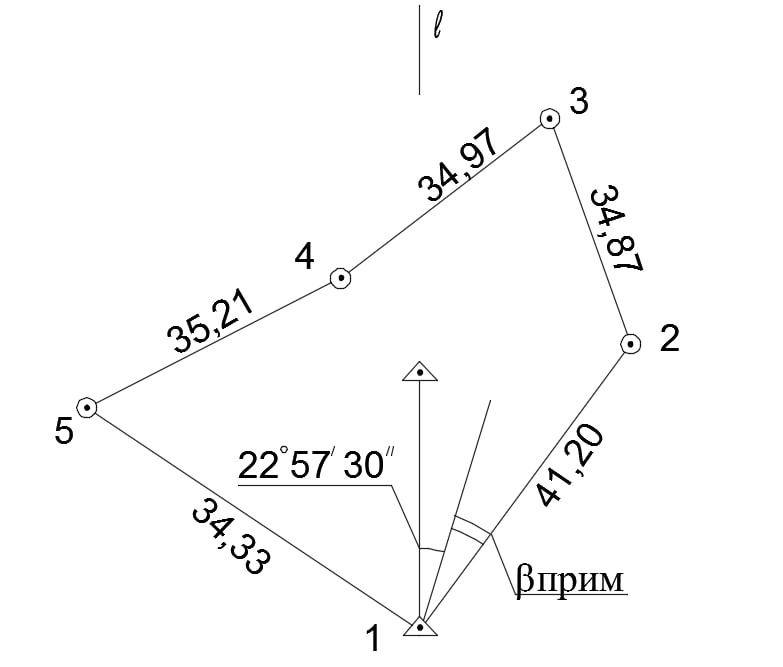
 Обработка журнала теодолитного хода Таблица 1 3)Теоретическая сумма углов любого многоугольника может быть вычислена по формуле: Σβтеор = 180* (n – 2), где n – число углов. 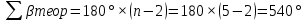 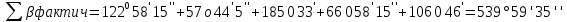 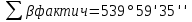 4)Разность фактической суммы углов и теоретической называется угловой невязкой. Фактическая угловая невязка должна быть меньше или равна допустимому значению. Величина допустимой угловой невязки определяется по формуле: fβдоп = ± 2с √n, где с – инструментальная погрешность прибора (в данном случае с = 30′′), n – число точек хода. Угловая невязка: 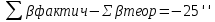 Допустимое значение угловой невязки: 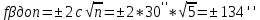 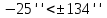 Фактическая угловая невязка меньше допустимого значения, она распределяется с обратным знаком поровну на все углы полигона. 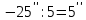 (добавляем к каждому внутреннему углу) (добавляем к каждому внутреннему углу)Сумма исправленных внутренних углов соответствует теоретической. Ведомость вычисления координат замкнутого теодолитного хода
Таблица 2 5)Вычисляем дирекционные углы направлений теодолитного хода. Дирекционный угол первого направления, соединяющего точки 1 (твердую) и 2, можно вычислить, зная дирекционный угол твердого направления и примычный угол, по формуле: α 1-2 = α тв. + β прим. Значение примычного угла: 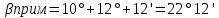 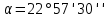 6) 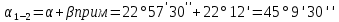 7)Последующие дирекционные углы (правые по ходу, при прокладывании хода по часовой стрелке) вычисляются по формуле: α n = α n-1 + 180 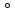 – β n – β nПри прокладывании хода против часовой стрелки (левые по ходу углы) формула видоизменяется: α n = α n-1 – 180 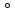 + β n + β n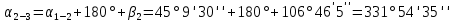 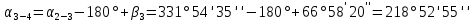 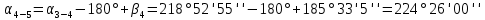 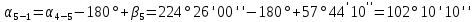 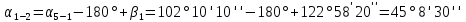 Контролем правильности вычислений является повторное получение дирекционного угла начальной стороны. 8)Вычислим периметр хода 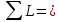 41,2+34,33+35,12+34,97+34,87=180,49 41,2+34,33+35,12+34,97+34,87=180,499)Следующий шаг – вычисление приращений координат точек теодолитного хода по формулам прямой геодезической задачи: ∆X = L * cos α, ∆Y = L * sin α, где L – горизонтальные проложения. Значения приращений округляем до сантиметров (0,01 м). ∆X1-5= 34,33*cos 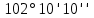 =-7,21 =-7,21∆X5-4= 35,12*cos 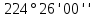 = -24,94 = -24,94∆X4-3= 34,97*cos 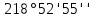 = -26,93 = -26,93∆X3-2= 34,87*cos 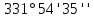 = 30,69 = 30,69∆X2-1= 41,2*cos 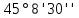 = 29,25 = 29,25∆Y1-5=34,33*sin 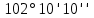 =33,64 =33,64∆Y5-4=35,12*sin 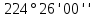 =-24,58 =-24,58∆Y4-3=34,97*sin218о 52' 55''= -22,03 ∆Y3-2=34,87*sin331о 54' 35''= -16,38 ∆Y2-1=41,2*sin45о 8' 30''= 58,86 10)Далее вычисляем невязки в приращениях координат по формулам fx = Σ∆x и fy = Σ∆y и абсолютную линейную невязку fабс= √fx2 + fy2. 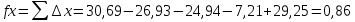 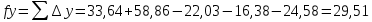 11) 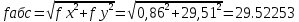 Оценка точности измерений проводится по относительной невязке полигона: f отн. = 1 / (ΣL :fабс.), где ΣL – периметр полигона. Допустимая относительная невязка определяется средством измерения длины. Так, для землемерной ленты она составит 1 / 2000. 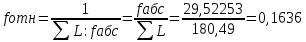 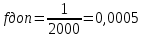  12) Так как относительная невязка не превышает допустимое значение, приступаем к уравниванию приращений координат, которое производится пропорционально длине стороны.  0,196 0,196 0,164 0,164 0,167 0,167 0,167 0,167 0,166 0,166 6,736 6,736 5,613 5,613 5,742 5,742 5,718 5,718 5,701 5,701Сумма поправок равна по модулю значениям невязок в приращениях fx и fy. 13)Вычисляем исправленные значения приращений и высчитываем плановые координаты точек теодолитного хода по формулам: Xn = Xn-1 + ∆x n-1 – n Yn = Yn-1 + ∆y n-1 – n X1=1000 Y1=2000 X5=X1+ΔX1-5=1000-7,21=992,79 X4=X5+ΔX5-4=990,99-24,94=966,05 X3=X4+ΔX4-3=967,25-26,93=940,32 X2=X3+ΔX3-2=941,23+30,69=971,92 X1=X2+ΔX2-1=972,61+29,25=1001,86 Y5=Y1+ΔY1-5=2000+33,64=2033,64 Y4=Y5+ΔY5-4=2033,17-24,58=2008,59 Y3=Y4+ΔY4-3=2007,29-22,03=1985,26 Y2=Y3+ΔY3-2=1983,93-16,38=1967,55 Y1=Y2+ΔY2-1=1969,2+58,86= | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||