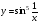Практ_8. Отчет к упражнению 1
 Скачать 95.74 Kb. Скачать 95.74 Kb.
|
Отчет к упражнению 1Для функции  создать M-File, вычисляющий приращение функции в точке создать M-File, вычисляющий приращение функции в точке  при приращениях аргумента при приращениях аргумента 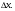 С помощью вызова M-File вычислить приращения функции в точках С помощью вызова M-File вычислить приращения функции в точках    при приращениях от 0 до 1 с шагом 0.1. при приращениях от 0 до 1 с шагом 0.1.Создаем скрипт функции delta.m: function df=delta(x0,dx) df=(x0+dx)^2-x0^2; end; Выполняем скрипт: clear all;close all;clc; dx=0:0.1:1; delta(0,dx) ans = Columns 1 through 9 0 0.0100 0.0400 0.0900 0.1600 0.2500 0.3600 0.4900 0.6400 Columns 10 through 11 0.8100 1.0000 delta(2,dx) ans = Columns 1 through 9 0 0.4100 0.8400 1.2900 1.7600 2.2500 2.7600 3.2900 3.8400 Columns 10 through 11 4.4100 5.0000 delta(-9,dx) ans = Columns 1 through 9 0 -1.7900 -3.5600 -5.3100 -7.0400 -8.7500 -10.4400 -12.1100 -13.7600 Columns 10 through 11 -15.3900 -17.0000 Отчет к упражнению 2Создать функцию, вычисляющую приращения функции 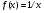 в точке 1 при различных приращениях аргумента. Вычислить приращения функции при приращениях аргумента от -0.5 до 0.5 с шагом 0.05. в точке 1 при различных приращениях аргумента. Вычислить приращения функции при приращениях аргумента от -0.5 до 0.5 с шагом 0.05. Создаем скрипт функции delta2.m: function df=delta2(dx) df=1./(1+dx)-1; end Выполняем скрипт: dx=-0.5:0.05:0.5; delta2(dx) ans = Columns 1 through 9 1.0000 0.8182 0.6667 0.5385 0.4286 0.3333 0.2500 0.1765 0.1111 Columns 10 through 18 0.0526 0 -0.0476 -0.0909 -0.1304 -0.1667 -0.2000 -0.2308 -0.2593 Columns 19 through 21 -0.2857 -0.3103 -0.3333 Отчет к упражнению 3Создать функцию, зависящую от точки  и приращения и приращения  вычисляющую предел отношения приращения функции к приращению аргумента для функции вычисляющую предел отношения приращения функции к приращению аргумента для функции 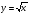 . Вычислить отношение приращения функции к приращению аргумента для каждой из точек 1; 0,5; 2 при приращениях аргумента 0,1; 0,01; 0,001. . Вычислить отношение приращения функции к приращению аргумента для каждой из точек 1; 0,5; 2 при приращениях аргумента 0,1; 0,01; 0,001.Создаем скрипт функции delta3.m: function l=delta3(x0,dx) l=(sqrt(x0+dx)-sqrt(x0))./dx; Выполняем скрипт: delta3(1,0.1) ans = 0.4881 delta3(1,0.01) ans = 0.4988 delta3(1,0.001) ans = 0.4999 delta3(0.5,0.1) ans = 0.6749 delta3(0.5,0.01) ans = 0.7036 delta3(0.5,0.001) ans = 0.7068 delta3(2,0.1) ans = 0.3492 delta3(2,0.01) ans = 0.3531 delta3(2,0.001) ans = 0.3535 Отчет к упражнению 4Создать функцию, зависящую от функции, точки и приращения, вычисляющую отношение приращения функции к приращению аргумента. Вычислить значения этой функции в точках 1, 2, 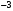 при приращениях аргумента 0,001, при приращениях аргумента 0,001,  для функций для функций  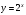 . .Создаем скрипт функции delta4.m: function l=delta4(fname,x0,dx) l=(feval(fname,x0+dx)-feval(fname,x0))/dx; Создаем скрипт функции myfun1.m: function f=myfun1(x) f=x^(1/3); Создаем скрипт функции myfun2.m: function f=myfun2(x) f=2^x; Выполняем скрипт: delta4('myfun1',1,0.001) ans = 0.3332 delta4('myfun1',1,-0.001) ans = 0.3334 delta4('myfun1',2,0.001) ans = 0.2100 delta4('myfun1',2,-0.001) ans = 0.2100 delta4('myfun1',-3,0.001) ans = -0.0801 - 0.1388i delta4('myfun1',-3,-0.001) ans = -0.0801 - 0.1388i delta4('myfun2',1,0.001) ans = 1.3868 delta4('myfun2',1,-0.001) ans = 1.3858 delta4('myfun2',2,0.001) ans = 2.7735 delta4('myfun2',2,-0.001) ans = 2.7716 delta4('myfun2',-3,0.001) ans = 0.0867 delta4('myfun2',-3,-0.001) ans = 0.0866 Отчет к упражнению 5Создать функцию, зависящую от функции и точки, вычисляющую значение производной функции в точке по определению. Для функций и точек из упражнения 4 вычислить значения производных. Заполнить таблицу, вставив вместо упр4 и упр5 результаты соответствующих упражнений. Создаем скрипт функции delta5.m: function l=delta5(fname,x0) dx=sym('dx'); l=limit((feval(fname,x0+dx)-feval(fname,x0))/dx,dx,0); end Выполняем скрипт: delta5('myfun1',1) ans = 1/3 delta5('myfun1',2) ans = NaN delta5('myfun1',-3) ans = -Inf delta5('myfun2',1) ans = 2*log(2) delta5('myfun2',2) ans = 4*log(2) delta5('myfun2',-3) ans = 1/8*log(2)
Отчет к упражнению 6Вычислить производные и их значения в точке  для следующих функций для следующих функцийа)  syms x; y=diff('(arctan(sqrt(x)))^2',x,1) y = atan(x^(1/2))/x^(1/2)/(1+x) subs(y,'x',0.5) ans = 0.5803 б)  . . syms x; y=diff('3^arcsin(x^2)',x,1) y = 2*3^asin(x^2)*x/(1-x^4)^(1/2)*log(3) subs(y,'x',0.5) ans = 1.4977 Отчет к упражнению 7Создать файл-функцию для построения касательной к графику функции в точке. Входными аргументами функции являются строка с символическим представлением функции одной переменной  и числовое значение абсциссы точки и числовое значение абсциссы точки 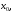 в которой следует провести касательную. Файл-функция выводит в одном графическом окне графики функции и касательной к ней в заданной точке на промежутке в которой следует провести касательную. Файл-функция выводит в одном графическом окне графики функции и касательной к ней в заданной точке на промежутке  Алгоритм файл-функции включает: Алгоритм файл-функции включает:1) Нахождение производной символически заданной функции. 2) Формирование символического выражения для касательной и подстановки в него значения производной, абсциссы и ординаты точки, в которой проводится касательная. 3) Построение графика функции и касательной к нему в указанной точке на указанном промежутке. function y=touch(fname,x0) hold on;grid on; syms x; y1=diff(fname,x,1); f=@(x)fname; y0=feval(f,x); y11=subs(y1,'x',x0); y00=subs(y0,'x',x0); y=y00+y11*(x-x0); xp=x0-1:0.1:x0+1; yp=subs(y,'x',xp); plot(xp,yp); yp=subs(y0,'x',xp); plot(xp,yp,'m'); end Используя созданную файл-функцию, построить график функции и касательную к нему для следующих функций: а)   touch('(cos(3*x))^3',pi/4);  б) 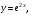  . .touch('exp(2*x)',1);  Отчет к упражнению C1Создать функцию, зависящую от функции, точки и приращения, вычисляющую отношение приращения функции к приращению аргумента. Вычислить значения этой функции в точках 1, 2, 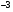 при приращениях аргумента 0,001, при приращениях аргумента 0,001, 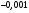 для функции для функции 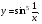 Создаем скрипт функции: function l=c1(fname,x0,dx) l=(feval(fname,x0+dx)-feval(fname,x0))/dx Выполняем скрипт: y=@(x)(sin(1/x))^5; c1(y,1,0.001); l = -1.3524 c1(y,1,-0.001); l = -1.3565 c1(y,2,0.001); l = -0.0579 c1(y,2,-0.001); l = -0.0580 c1(y,-3,0.001); l = -0.0060 c1(y,-3,-0.001); l = -0.0060 Отчет к упражнению C2Заполнить таблицу, вставив вместо С1 результаты упражнения С1, а вместо С2 значение производной функции в указанной точке, вычисленное по определению. Создаем скрипт функции: function l=c2(fname,x0) syms dx; l=limit((feval(fname,x0+dx)-feval(fname,x0))/dx,dx,0) end Выполняем скрипт: y=@(x)(sin(1/x))^5; c2(y,1); l = NaN c2(y,2); l = NaN c2(y,-3); l = NaN
Отчет к упражнению C3Вычислить производную функции  и ее значение в точке и ее значение в точке  syms x; y=diff('log(x^2+1)/log(3)/(arccos(sin(x)))^3',x,1) y = 2*x/(x^2+1)/log(3)/(1/2*pi-asin(sin(x)))^3+3*log(x^2+1)/log(3)/(1/2*pi-asin(sin(x)))^4*cos(x)/(1-sin(x)^2)^(1/2) subs(y,'x',0.5) ans = 1.0566 | ||||||||||||||||||||||||||||||||