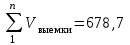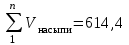Геодезия КР №1. Контрольная работа по учебному курсу Геодезия 2 Вариант 12 (при наличии) Студент

• Название: Контрольная работа по учебному курсу Геодезия 2 Вариант 12 (при наличии) Студент
• Дата: 02.03.2023
• Размер: 1.2 Mb.
• Имя файла: Геодезия КР №1.docx
• Тип: Контрольная работа; #964923

М ИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
федеральное государственное бюджетное образовательное учреждение

высшего образования

«Тольяттинский государственный университет»

Архитектурно-строительный институт
Центр архитектурных, конструктивных решений и организации строительства
КОНТРОЛЬНАЯ РАБОТА
по учебному курсу «Геодезия 2»
Вариант 12 (при наличии)

Студент	К.А. Меньшаков (И.О. Фамилия)
Группа	СТРбвд-2003а (И.О. Фамилия)
Преподаватель	Л.Н. Грицкив (И.О. Фамилия)

Тольятти 2022

Оглавление

Вертикальная планировка строительной площадки – 2 страница
Ответы по теоретической части – 15 страница
Библиографический список – 21 страница


Вертикальная планировка строительной площадки


Исходные данные:
Журнал нивелирования поверхности по квадратам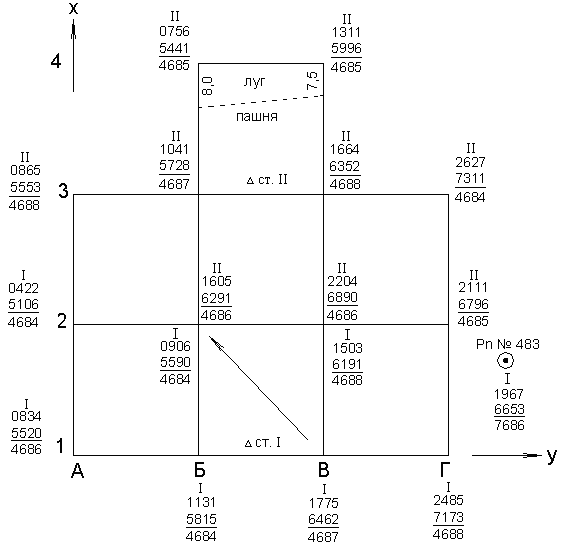

1. 
   Отметка репера № 483 H_Pn = 71,387 м;
   
2. 
   Топографический план построить в масштабе – 1:500, высота сечения рельефа – 0,25 м;
   
3. 
   Длина стороны квадрата а = 20 м
   

Исходные данные для вычисления отметок вершин квадратов и построения топографического плана:

1. 
   М 1:500
   
2. 
   l = 20 м
   
3. 
   h_ср = 0,5 м
   
4. 
   H_Pn = 71,387 м;
   
5. 
   l_чRp483=1967
   
6. 
   l_крRp483=6653
   

Камеральная обработка результатов полевых измерений

1. 
   Вычисление горизонта прибора на I станции
   

Вычисляют горизонт прибора на I станции, используя отметку репера №483 и отсчеты по красной и черной сторонам рейки, установленной на репере

,
,
НГПч=71,387+1,967=73,354м
,
НГПкр=71,387+6,653=78,040м

2. 
   Вычисление отметок всех вершин квадратов пронивелированных с I станции
   

   ,
   ,
   .
   	НА1чер= 73,354 м – 0,834 м = 72,520 м	НА1ср= 72,520 м
   	НА1кр= 78,040 м – 5,520 м = 72,520 м
   	НБ1чер= 73,354 м – 1,131 м = 72,223 м	НБ1ср= 72,224 м
   	НБ1кр= 78,040 м – 5,815 м = 72,225 м
   	НВ1чер= 73,354 м – 1,775 м = 71,579 м НВ1кр= 78,040 м – 6,462 м = 71,578 м	НВ1ср= 71,578 м
   	НГ1чер= 73,354 м – 2,485 м = 70,869 м НГ1кр= 78,040 м – 7,173 м = 70,867 м	НГ1ср= 70,868 м
   	НА2чер= 73,354 м – 0,422 м = 72,932 м	НА2ср= 72,933 м
   	НА2кр= 78,040 м – 5,106 м = 72,934 м
   	НБ2чер= 73,354 м – 0,906 м = 72,448 м	НБ2ср= 72,449 м
   	НБ2кр=78,040 м – 5,590 м = 72,450 м
   	НВ2чер= 73,354 м – 1,503 м = 71,851 м	НВ2ср= 71,850 м
   	НВ2кр=78,040 м – 6,191 м = 71,849 м

3. 
   Выполняют контроль взятия отсчетов на связующих точках Б2 и В2 пронивелированых с двух станций:
   

,

где l – отсчет по рейке.
Вершина квадрата Б2: 0906 мм + 6291 мм >1605 мм + 5590 мм
7197 мм > 7195 мм
Разность составляет 2 мм. Допустимое расхождение составляет 5 мм.
Вершина квадрата точка В2: 2204 мм + 6191 мм = 1503 мм + 6890 мм
8395 мм < 8393 мм
Разность составляет 2 мм. Допустимое расхождение составляет 5 мм
Вывод: контроль удовлетворяет требованиям, значит вершины квадратов: Б2 и В2 можно использовать для вычисления горизонта прибора на II станции.

4. 
   Вычисление горизонта прибора на II станции
   

Вычисляют горизонт прибора на II станции, используя вычисленные отметки связующих точек (вершин) Б2, Б3 и результаты нивелирования этих вершин на II станции:
вершина Б2:
Н_ГПч= Н_Б2+l_чБ2=72,449+1,605=74,054
Н_ГПкр= Н_Б2+l_крБ2=72,449+6,291=78,740
вершина В2:
Н_ГПч= Н_В2+l_чВ2=71,850+2,204=74,054
Н_ГПкр= Н_В2+l_крВ2=71,850+6,890=78,740

5. 
   Вычисление отметок всех вершин квадратов пронивелированных с II станции
   

,
,
.
НГ2чер= 74,054 м – 2,111 м = 71,943 м	НГ2ср= 71,943 м
НГ2кр=78,740 м – 6,796 м = 71,944 м
НА3чер= 74,054 м – 0,865 м = 73,189 м	НА3ср= 73,188 м
НА3кр= 78,740 м – 5,553 м = 73,187 м
НБ3чер= 74,054 м – 1,041 м = 73,013 м	НБ3ср= 73,012 м
НБ3кр= 78,740 м – 5,728 м = 73,012 м
НВ3чер= 74,054 м – 1,664 м = 72,390 м	НВ3ср= 72,389 м
НВ3кр= 78,740 м – 6,352 м = 72,388 м
НГ3чер= 74,054 м – 2,627 м = 71,427 м	НГ3ср= 71,428 м
НГ3кр= 78,740 м – 7,311 м = 71,429 м
НБ4чер= 74,054 м – 0,756 м = 73,298 м	НБ4ср= 73,298 м
НБ4кр= 78,740 м – 5,441 м = 73,299 м
НВ4чер= 74,054 м – 1,311 м = 72,743 м	НВ4ср= 72,743 м
НВ4кр= 78,740 м – 5,996 м = 72,744 м

6. 
   Построение топографического плана по результатам нивелирования строительной площадки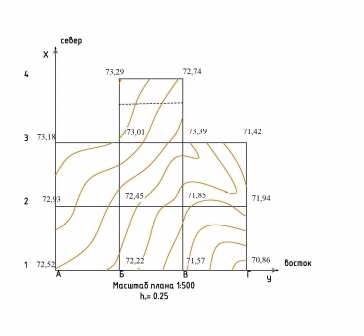
   
   

Проектирование горизонтальной площадки


1. Вычисление проектной отметки горизонтальной площадки.
Вычисляют проектную отметку горизонтальной площадки по формуле:

,

где Н_min – наименьшая из фактических отметок вершин квадратов, n – число квадратов.
Для облегчения расчетов вводят в расчетную формулу понятие: условная отметка h. Вычисляют условную отметку для каждой вершины квадрата:

h = Hфакт – Нmin.

Согласно топографическому плану (приложение 1) вычисляют: h₁, h₂, h₃, h₄
h₁ – сумма отметок вершин квадратов, принадлежащих только одному квадрату;

h1 = HА1 + НА3 + НГ1 + НГ3 + НБ4 + НВ4.

h₂ – сумма отметок вершин квадратов общих для двух смежных квадратов:

h2 = НБ1 + НВ1 + НА2 + НГ2.

Полученную сумму h₂ подставляют в формулу:
h₃ – сумма отметок вершин квадратов общих для трех смежных квадратов:

h3 = НБ3 + НВ3.
Полученную сумму h3 подставляют в формулу: h4 – сумма отметок вершин, объединяющих четыре квадрата; h4 = НБ2 + НВ2.

Полученную сумму h₄ подставляют в формулу:
В рассматриваемом примере Н_min = 70,87 м.
h₁= 1,65 м + 2,32 м + 0 м + 0,56 м + 2,43 м + 1,87 м = 8,83 м;
h₂ = 1,35 м + 0,71 м + 1,99 м + 1,08 м = 5,13 м;
h₃= 2,14 м + 1,51 м= 3,65 м;
h₄= 1,58 м + 0,98 м = 2,56 м.
Подставляют все полученные величины в формулу вычисления проектной отметки горизонтальной площадки:
Н_пр.гор =70,87+  =72,31
Таким образом, проектная отметка горизонтальной площадки:
Н_пр.гор = 72,31 м.
2. Вычисление рабочих отметок всех вершин квадратов
Вычисляют рабочие отметки всех вершин квадратов, показывающих высоту насыпи (+) или глубину выемки (–) как разность проектной и фактических отметок по формуле:

.
Например, рабочую отметку вершины А1 вычисляют: hА1= 72,31 м – 72,52 м = - 0,21 м.

Правильность вычисления рабочих отметок контролируют по формуле:

.

2. 
   Вычисление положения точек нулевых работ
   Вычерчивают картограмму земляных работ. Картограмма земляных работ – это графический документ вертикальной планировки. Составляется на основе топографического плана строительной площадки. Для этого вычерчивают сеть квадратов и в каждой вершине подписывают фактические (черные) отметки и вычисленные рабочие отметки. Проектную отметку подписывают ниже картограммы.
   

Вычисляют положение точек нулевых работ. Ноль работ – это точка пересечения фактической линии (линии Земли) и проектной линии. Определение положения точек нулевых работ проводят между смежными рабочими отметками сторон квадратов, имеющими разные знаки.
Положение точек нулевых работ определяют аналитическим способом по формуле:

,  .

Контроль вычислений:
l₁ + l₂ = l
где h₂ – рабочая отметка выемки; h₁ – рабочая отметка насыпи; l – длина стороны квадрата; l₁ и l₂ – расстояния, определяющие положение точек нулевых работ на стороне квадрата. (рис. 2)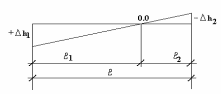


Рис. 2. Определение положения точек нулевых работ
Пример вычисления точки нулевых работ:
Для стороны между вершинами А1–Б1 положение точки нулевых работ определяют:

l1 =  =14 l2 =  =6

Точка нулевых работ находится на расстоянии 14 м от вершины квадрата с рабочей отметкой -0,21 м.
Соединив точки нулевых работ прямыми линиями, получают линию нулевых работ. Объем земляных масс можно вычислить методом четырехгранных или трехгранных призм.
Объем четырехгранной призмы определяют по формуле:

,

где   – средняя высота однородной призмы, вычисляют как среднюю арифметическую из рабочих отметок;S – площадь основания призмы.
Объем трехгранной призмы определяют по формуле:

.

Объем пятигранных призм в смешанных квадратах можно вычислять как разность объемов четырехгранных и трехгранных призм.
Вычисление объемов земляных масс насыпей и выемок выполняют для каждого квадрата или части его, используя вышеприведенные формулы.
После вычисления объемов отдельных фигур находят общий объем насыпи и выемки. Контролем вычисления объемов земляных масс является примерное равенство объемов насыпи и выемки. Допускается расхождение в пределах до 5% от общего объема насыпи и выемки (Таблица 2).

Таблица 2
Ведомость вычисления объемов земляных масс

с	Площадь фигуры, м2	Средняя рабочая отметка	Объемы земляных работ, м3
			Выемка (-)	Насыпь (+)
1	140	+0,92	-	128,8
2	150	+0,47	-	70,5
3	50	-0,18	-9,0	-
4	60	-0,37	-22,2	-
5	400	-0,46	-184,0	-
6	140	+0,84	-	117,6
7	120	+0,39	-	46,8
8	80	-0,24	19,2	-
9	60	-0,43	25,8	-
10	400	-0,51	204,0	-
11	40	-0,25	10,0	-
12	150	-0,21	31,5	-
13	160	+0,16	-	25,6
14	50	+0,24	-	12,0
15	120	+0,85	-	102,0
16	164	+0,46	-	75,4
17	56	-0,24	13,4	-
18	60	+0,56	-	33,6
19	21	+0,10	-	2,1
20	39	-0,19	7,4	-
21	140	-0,43	60,2	-
22	200	-0,46	92,0	-
	 = 2800	-

Вычисляем объемы выемок и насыпей:

,  .

Определяем абсолютную величину их разности:

V=31,03

Отношение V к общей сумме насыпей и выемок, выраженное в процентах, характеризует баланс земляных масс:

=2,8%

Ответы по теоретической части

1. Какая съемка называется тахеометрической? В чем сущность тригонометрического нивелирования? Ответ дополнить схемой.

Тахеометрическая съемка представляет собой топографическую, т.е. контурно-высотную съемку, в результате которой получают план местности с изображением ситуации и рельефа. Тахеометрическая съемка выполняется самостоятельно для создания планов небольших участков местности в крупных масштабах либо в сочетании с другими видами работ. Ее применение особенно выгодно для съемки узких полос местности при изысканиях трасс железных и автомобильных дорог, линий электропередач, трубопроводов и других протяженных объектов.
Быстрота измерений при тахеометрической съемке достигается тем, что положение снимаемой точки местности в плане и по высоте определяется при одном наведении трубы прибора на рейку, установленную на точке. Тахеометрическая съемка выполняется при помощи технических теодолитов или тахеометров.
При использовании технических теодолитов сущность тахеосъемки сводится к определению пространственных полярных координат точек местности и последующему нанесению этих точек на план. При этом горизонтальный угол между начальным направлением и направлением на снимаемую точку измеряется с помощью горизонтального круга, вертикальный угол – при помощи вертикального круга теодолита, а расстояние до точки – дальномером. Таким образом, плановое положение снимаемых точек определяется полярным способом, а превышения точек – методом тригонометрического нивелирования, осуществляемого с помощью наклонного луча визирования.
Принцип тригонометрического нивелирования заключается в следующем. Пусть требуется определить превышение h точки В над точкой А (рисунок 5). Над точкой А устанавливается в рабочее положение теодолит, а в точке В отвесно – рейка. Измеряется высота прибора i и зрительной трубой теодолита визируют на рейку на высоту визирования v. С помощью вертикального круга измеряют вертикальный угол n, а дальномером - наклонное расстояние D либо его горизонтальную проекцию d по формуле:

  .
Как следует из схемы рисунка:
h + v = h’ + i.
h = h’ + i – v.
Поскольку
h’ = d tgn.
h = d tgn + i – v.
При i = v, т.е. при визировании на высоту прибора, отмеченную на рейке формула примет вид:
h = d tgn.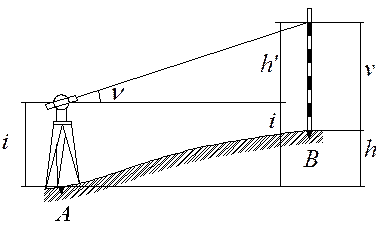



Рисунок 5. Принцип тригонометрического нивелирования.

При использовании специальных тахеометров горизонтальные проложения и превышения получаются автоматически путем взятия отсчетов по рейке с помощью номограммных кривых. Преимущества тахеосъемки по сравнению с другими видами топографических съемок заключается в том, что она может выполняться при неблагоприятных погодных условиях. Кроме того, камеральные работы могут выполняться другим исполнителем вслед за производством полевых измерений, что позволяет сократить сроки составления плана снимаемой местности.
Основным недостатком тахеосъемки является то, что составление плана местности выполняется в камеральных условиях на основании только результатов полевых измерений и зарисовок. При этом нельзя своевременно выявить допущенные промахи путем сличения плана с местностью.


2. Какие точки круговой кривой называются главными? Как определяются данные для разбивки главных точек кривой?

Главными точками круговой кривой являются начало круговой кривой (НКК), конец круговой кривой (ККК) и середина круговой кривой (СКК).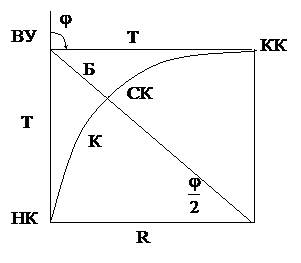



Рисунок 6. Главные точки круговой кривой

На плане и на местности эти точки могут быть получены, если известны следующие элементы кривой:
1 - угол поворота трассы φ;
2 - радиус круговой кривой R;
3 - расстояние от вершины угла поворота ВУ до начала или конца кривой, которое называется тангенс Т;
4 - длина кривой, расстояние от ее начала до ее конца К;
5 - расстояние от вершины угла поворота до середины кривой, которое называется биссектриса кривой Б;
6 - домер, показывающий, на сколько путь от начала до конца кривой по касательной больше, чем по кривой Д.
Угол поворота трассы измеряют при трассировании, а величину радиуса кривой (R) выбирают в соответствии с техническими условиями.
Остальные элементы круговой кривой могут быть определены из прямоугольного треугольника (О - НКК - ВУ) на рисунке 6 по следующим формулам:
Т = R tg φ / 2,
К = π R φ / 180º ,
Б = R / cosφ / 2 - R,
Д = 2Т - К.


3. В каких случаях применяется метод нивелирования поверхности по квадратам? Как строится сеть квадратов?


Нивелирование поверхности — один из способов топографической съемки, при котором на местности по определенному правилу располагают точки, высоты которых определяют геометрическим нивелированием. Наибольшее практическое применение имеет метод квадратов и метод магистралей с поперечными профилями. Создание плана по результатам нивелирования по квадратам начинают с разбивки в заданном масштабе сетки квадратов, у каждой выписывают округленную до сантиметра высоту. Согласно абрису наносят и вычерчивают в условных знаках ситуацию, а затем путем интерполирования горизонталями изображают рельеф.
Топографическую съемку небольших участков равнинной местности с небольшим количеством контуров при высоте сечения рельефа через 0,1; 0,25; 0,5 м выполняют нивелированием поверхности по квадратам, прямоугольникам, характерным линиям рельефа и т. п. Отметки пикетов во всех способа определяют точек.
При нивелировании по квадратам геометрическим нивелированием, различие состоит в методе определения планового положения и мерным прибором на местности разбивают сетку квадратов, в вершинах квадратов забивают колышки. Сначала строят квадраты со сторонами 100, 200 или 400 м, а затем получая более мелкие квадраты со сторонами 40 м при съемке в масштабе 1:2000, 20 м — при съемке в масштабе 1:1000 и 1:500. При разбивке квадратов выполняют съемку ситуации. Результаты съемки фиксируют в абрисе.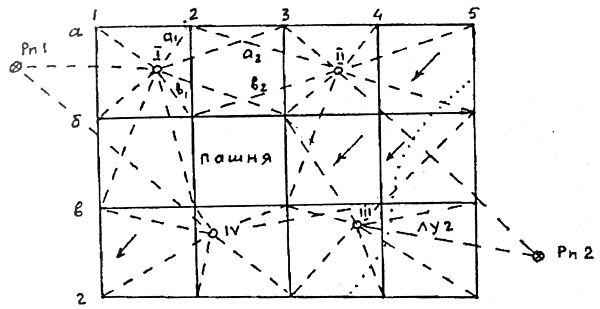



Рис. 7. Абрис нивелирования поверхности по квадратам (стрелками показано направление скатов).
Нивелир устанавливают так, чтобы с меньшего количества станций выполнить съемку всего участка. Установив нивелир на станции I, берут отсчет по рейке, поставленной на опорной высотной точке (например на Рп I) и вычисляют:
ГП = Нрn + а,
где Нрn — отметка репера; а — отсчет по рейке, установленной на репере. У номеров вершин квадратов выписывают отсчеты по рейкам, установленным на них, в абрисе штриховыми линиями показывают, на какие вершины квадратов выполнено нивелирование с данной станции. Отметки вершин квадратов вычисляют по формуле:
Нi = ГП - а
Подобным образом выполняют нивелирование и с других станций с обязательным определением ГП на каждой станции по опорным высотным пунктам или связующим точкам. С каждой последующей станции нивелируют несколько связующих точек, при этом а1+ b2 = а2 + b1, расхождение между этими суммами не должно превышать 10 мм.

Библиографический список

1. 
   Федотов, Г.А. Инженерная геодезия / Г.А. Федотов. – М. : Высшая школа, 2009. – 463 с.
   
2. 
   Клюшин, Е.Б. Инженерная геодезия / Е.Б. Клюшин [и др.]. – М. : Academia, 2004. - 479 с.
   
3. 
   Хаметов, Т.И. Геодезическое обеспечение проектирования, строительства и эксплуатации зданий и сооружений / Т.И. Хаметов. – М. : АСВ, 2002.
   
4. 
   Кулешов, Д.А. Инженерная геодезия / Д.А. Кулешов, Г.Е. Стрельников, Г.Е. Рязанцев. – М. : Картгеоцентр – геодезиздат, 1996. – 303 с.
   
5. 
   Федоров, В.И. Инженерная геодезия / В.И. Федоров, П.И Шилов. – М. : Недра, 1982. – 356 с.
   
6. 
   Хейфец, В.С. Практикум по инженерной геодезии / В.С. Хейфец, Б.Б. Данилевич. – М. : Недра, 1979. – 331 с.
   
7. 
   Закатов, П.С. Инженерная геодезия / П.С. Закатов. – М. : Недра, 1976. – 582 с.
   
8. 
   Условные знаки для топографических планов масштабов 1:500, 1:1000, 1:2000, 1:5000 (Главное управление геодезии и картографии при Совете Министров СССР). – М. : Недра, 1973. – 144 с.
   
9. 
   Пятизначные таблицы натуральных значений тригонометрических функций (Главная редакция физико-математической литературы). – М. : Наука, 1978. – 367 с.