КР_Вариант_14. КОнтрольная работа по учебному курсу Геодезия 2 Вариант 14 Студент (И. О. Фамилия)
 Скачать 0.51 Mb.
|
1 2  МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ федеральное государственное бюджетное образовательное учреждение высшего образования «Тольяттинский государственный университет» Архитектурно-строительный институт Центр архитектурных, конструктивных решений и организации строительства КОнтрольная работа по учебному курсу «Геодезия 2» Вариант 14
Тольятти 2021 Вариант №14 1 В каких случаях применяется метод нивелирования поверхности по квадратам? Как строится сеть квадратов? Данный метод используют при топографической съемке открытых участков местности с размеренным рельефом в больших масштабах (1:500--1:5000) с малой (0,1--0,5 м) высотой сечения рельефа с целью составления проекта вертикальной планировки и подсчета размеров земельных работ. Последовательность работ при нивелировании по квадратам: - рекогносцировка участка съемки; - разбивка сетки квадратов и съемки ситуации; - планово-высотная привязка сетки квадратов; - съемка рельефа; - расчетно-графические работы. Рекогносцировка участка съемки. На этом этапе работ оценивают возможность без помех разбить сетку квадратов и произвести геометрическое нивелирование, выбирают начальное направление одной из сторон сетки, станции нивелирования, связующие точки, а также оптимальный вариант привязки сетки квадратов к пунктам плановой и высотной геодезической сети. Разбивка сетки квадратов и съемка ситуации. Размеры разбиваемых на местности квадратов (от 10ґ10 м до 100ґ100 м) зависят от характера рельефа местности, заданной высоты сечения, площади участка под застройку и требований к точности изображения рельефа. Обычно начинают с разбивки внешнего полигона в виде прямоугольника или квадрата. Для этого вдоль границы снимаемого участка закрепляют опорную линию (А1-А5) Теодолит устанавливали в начальную точку А1 и ориентировали по начальному направлению А1-А5. В створе этой линии через 20 м забивали колышки, т.е. закрепляли точки А2, А3 и т.д. В точках А1 и А5 при помощи теодолита откладывали прямые углы и откладывали отрезки А1- Д1 и А5-Д5. Для контроля измеряли сторону Д1-Д5, ее длина не отличалась от проектной (80 м) более чем на 1:2000. Теодолит последовательно устанавливали в точках А2, А3 и т.д. и по аналогии закрепляли внутренние вершины квадратов. При необходимости на сторонах квадратов в точках перегиба рельефа местности закрепляют плюсовые точки. При длинах сторон внешнего полигона до 300 м разбивку заполняющих квадратов комфортно делать длинноватыми тросами, размеченными через расстояния, равные длине стороны квадрата. Одновременно с разбивкой пикетов делается съемка ситуации линейными промерами от сторон квадратов до соответствующих точек контуров и местных предметов. Результаты съемки заносят в абрис, на котором также демонстрируют стрелками направление скатов. Вершины квадратов закрепляются колышками высотой 10 см, которые забивают так, чтобы над поверхностью земли оставалось примерно 1,5 см 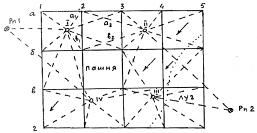 Планово-высотная привязка сетки квадратов. Для того чтобы топографический план был построен в принятой системе координат и высот, съемочное обоснование должно быть привязано к опорной геодезической сети. С этой целью сетка квадратов, являющаяся съемочным обоснованием, соединяется привязочными ходами к пунктам плановой и высотной основы. Съемка рельефа. Перед началом нивелирования на листе плотной бумаги составляют схему квадратов, которая одновременно является и полевым журналом. Места для станций нивелирования выбирают так, чтобы с каждой из них можно было выполнить нивелирование вершин нескольких квадратов. При этом каждые две смежные станции должны иметь общие связующие точки, которые необходимы для передачи отметок на последующие станции. Опорный ход замкнутый В данном случае для пяти станций связующими точками выбраны вершины квадратов А2, В4, Г3, Д5 (см. рис. 1). На схеме выделяют опорный разомкнутый ход, проходящий по связующим точкам (от Rp 1 по А2, В4, Г3, Д5 до Rp 2). На рис. 1 видно, что связующие точки нивелировались дважды со смежных станций. Пунктирные линии, соединяющие станции с соответствующими вершинами квадратов, схематично изображают визирные линии при нивелировании остальных вершин квадратов. Связующие точки нивелируются с контролем по двум сторонам реек. При нивелировании вершин квадратов рейку последовательно устанавливали на колышек и брали отсчеты по черной стороне рейки. Все отсчеты записывались на схеме нивелирования около соответствующей вершины. 2. Что называется горизонтом прибора? Как вычисляются отметки через превышение и горизонт прибора? Ответ дополнить схемой. Высота визирной оси над уровнем моря или над условным уровнем называется горизонтом прибора. Как видно из рис.1, горизонт прибора, т. е. горизонт прибора равен высоте точки плюс взгляд (отсчет по рейке) на эту точку. 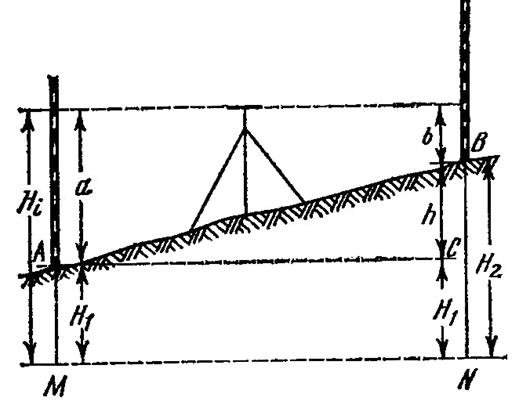 Зная горизонт прибора, легко найти высоту любой точки, на которую был сделан взгляд. Из рис.1 видно, что, т. е. высота точки равна горизонту прибора минус взгляд на эту точку. Таким образом, по высоте какой-либо точки и по взглядам на нее и на другие точки высоты последних могут быть получены двояко: по превышениям и по горизонту прибора. Вычислять высоты точек по горизонту прибора очень удобно, когда были сделаны взгляды на несколько точек с одной станции (точки стояния прибора) и одна из них имеет известную высоту. При нивелировании находят разности высот (превышения) между точками; по данной высоте начальной точки и по превышениям относительно нее других точек получают высоты всех остальных точек местности. В геометрическом нивелировании превышения определяются отсчетами по вертикальным рейкам горизонтальной линией визирования нивелира. Различают нивелирование из «середины» и «вперед». Геометрическое нивелирование из середины. Для определения превышения точки В над точкой А (рис.1) поставим в точках А и В отвесно рейки, разделенные на сантиметры, а между ними примерно на одинаковых расстояниях - нивелир. Направив последовательно установленную горизонтально визирную ось прибора на обе рейки, делаем отсчеты по ним a и b. Из рис.1 видно, что искомое превышение h определяется из равенства. Если считать условно точку А задней, а точку В - передней, то можно сказать, что превышение передней точки над задней равно взгляду (отсчету по рейке) назад минус взгляд (отсчет) вперед. Если превышение по указанной формуле окажется положительным, то это покажет, что передняя точка лежит выше задней и, следовательно, линия АВ повышается. Отрицательное превышение означает, что точка В ниже точки А, т.е. линия АВ понижается. Зная высоту точки А и превышение h над ней точки В, получают высоту точки В по формуле, т.е. высота последующей точки равна высоте предыдущей точки плюс соответствующее превышение. Нивелирование вперед. Иногда нивелир устанавливают так, что окуляр зрительной трубы приходится по отвесу над точкой А (рис.2). Вертикальное расстояние i от центра окуляра при установленной горизонтально визирной оси зрительной трубы до точки А называется высотой прибора. 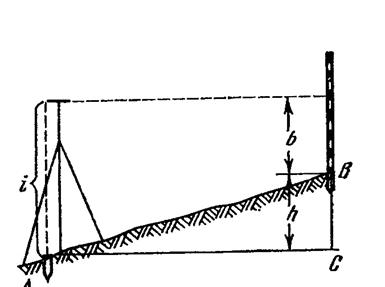 Пусть в точке В вертикально установлена рейка. Направив на нее горизонтальную визирную ось и сделав отсчет по рейке b, получим, т.е. в этом случае превышение равно высоте прибора минус взгляд вперед. Высоту прибора можно отсчитать по рейке или измерить рулеткой. Если передняя точка В выше задней А, то превышение положительно; при понижении местности от А к В превышение отрицательно. 3 Как вычисляется невязка в превышениях замкнутого нивелирного хода и разомкнутого нивелирного хода? Как вычислить допустимые невязки и как распределить поправки? Невязки в нивелирных ходах, их допустимость и распределение Рассмотрим разомкнутый ход нивелирования (рис.2.1). Измеренное превышение между начальной и конечной точками хода равно сумме превышений, измеренных на каждой станции, то есть  ,где 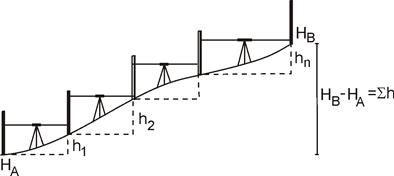 - превышение, измеренное на i-ой станции. Полученное таким образом превышение между начальной и конечной точками хода называют измеренной, или практической, суммой превышений. С другой стороны, если высота H0 начальной точки хода и высота  конечной точки хода известны, то в соответствии с определением превышения превышение между ними может быть определено как разность их высот: . Рис. 2.1. Сумма превышений Данное значение превышения между точками A и B называют теоретической суммой превышений. Очевидно, что измеренная сумма превышений должна равняться теоретической  .Но также очевидно, что вследствие ошибок измерений такое равенство будет выполняться только тогда, когда ошибки измерений полностью компенсируются. За крайне редкими исключениями такой компенсации ошибок не будет, и сумма измеренных превышений будет отличаться от теоретической суммы превышений, то есть будет иметь место соотношение  .Разность между измеренной суммой превышений и ее теоретическим значением называется невязкой превышений  .(В общем случае разность между результатом  измерений некоторой величины и ее теоретическим значением  называется невязкой:  . Пример: угловая невязка в треугольнике на плоскости есть разность между суммой его измеренных углов и 180°.)В замкнутом нивелирном ходе отметка начальной точки равна отметке конечной точки, то есть H0=Hn. Следовательно, теоретическая сумма превышений в замкнутом ходе равна  .Тогда невязка в замкнутом нивелирном ходе будет равна измеренной сумме превышений, то есть  .Очевидно, что величина невязки в нивелирном ходе будет зависеть от использованных приборов, тщательности выполненных измерений, внешних условий и ряда других факторов. При техническом нивелировании для оценки качества выполненных измерений превышений служит величина допустимой невязки, вычисляемая по эмпирической формуле  ,где L – число километров в ходе; говорят также, что L – длина хода, выраженная в километрах. Если на каждый километр нивелирного хода приходится большое число станций (более 25), то рекомендуется использовать другую формулу:  ,где n - общее число станций в ходе. Если полученная невязка превышений по модулю больше допустимой невязки, то есть имеет место соотношение  , то результаты измерений превышений не могут быть признаны удовлетворительными, и полевые измерения должны быть выполнены повторно. Если выполняется условие  , то результаты измерений считаются доброкачественными, выполненными надлежащим образом, и обработка хода может быть продолжена.Таблица 2.1. Пример обработки журнала технического нивелирования
Но если невязка превышений допустима и не равна нулю (  ), то мы имеем определенное противоречие: измеренная сумма превышений не равна теоретической сумме превышений, чего не может быть. Поэтому полученные результаты измерения превышений нужно привести в соответствие с требованиями геометрии и здравым смыслом, “исправить” их определенным образом. В таких случаях говорят, что нужно распределить невязку, ввести в измеренные значения некоторые поправки. При этом поправки должны вводиться таким образом, чтобы сумма исправленных превышений равнялась теоретической.Существует бесконечное число вариантов распределения поправок. При выборе такого варианта можно рассуждать следующим образом. Полевые измерения выполнялись одним и тем же прибором, по одной и той же методике, при одной и той же погоде, и прочих равных условиях, поэтому у нас нет оснований одним измерениям доверять меньше и вводить в них большие поправки, а другим измерениям доверять больше и вводить в них меньшие поправки. Представляется разумным и достаточно обоснованным считать результаты наших измерений равноточными и руководствоваться при этом принципом равенства поправок. Тогда во все измерения необходимо вводить одну и ту же поправку δ, которая может быть вычислена по формуле  ,где n – число станций в ходе. При этом говорят, что поправка в превышения равна невязке с противоположным знаком, деленной на число станций. Значения поправок округляются до 1 мм. После вычисления поправок в превышения выполняется их контроль, который сводится к проверке выполнения соотношения  ,то есть сумма поправок в превышения должна равняться невязке, взятой с противоположным знаком. Так как при обработке результатов технического нивелирования значения превышений и поправки в превышения округляются до 1 мм, может случиться так, что вследствие ошибок округления последнее соотношение не выполняется, тогда некоторые поправки увеличивают или уменьшают на 1 мм так, чтобы выполнялось равенство . Желательно, чтобы превышения с такими поправками располагались примерно равномерно по всему ходу нивелирования.Таким образом, можно считать, что в отдельном ходе поправки вводятся поровну во все измеренные превышения с округлением до 1 мм. Исходные данные для вычисления отметок вершин квадратов и построения топографического плана: М 1:500 l = 20 м hср = 0,25 м 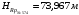 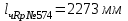 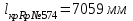 α0 = 120º00' i0 = 0,025 Вычисление горизонта прибора на I станции Вычисляют горизонт прибора на I станции, используя отметку репера №574 и отсчеты по красной и черной сторонам рейки, установленной на репере
Вычисление отметок всех вершин квадратов пронивелированных с I станции
Выполняют контроль взятия отсчетов на связующих точках Б2 и Б3 пронивелированых с двух станций:
где l – отсчет по рейке. Вершина квадрата Б3: 0461 мм + 5859 мм >1072 мм + 5245 мм 6320 мм > 6317 мм Разность составляет 3 мм. Допустимое расхождение составляет 5 мм. Вершина квадрата точка Б2: 0334 мм + 5732 мм = 0946 мм + 5120 мм 6066 мм = 6066 мм Вывод: контроль удовлетворяет требованиям, значит вершины квадратов: Б2 и Б3 можно использовать для вычисления горизонта прибора на II станции. Вычисление горизонта прибора на II станции Вычисляют горизонт прибора на II станции, используя вычисленные отметки связующих точек (вершин) Б2, Б3 и результаты нивелирования этих вершин на II станции: вершина Б3:
вершина Б2:
Вывод: средние значения ГП, полученные по результатам нивелирования вершин Б2 и Б3 принимают за окончательные и используют для вычисления отметок вершин квадратов, пронивелированных на станции II. Вычисление отметок всех вершин квадратов пронивелированных с II станции
Построение топографического плана по результатам нивелирования строительной площадки Для построения топографического плана по результатам нивелирования поверхности строительной площадки вычерчивают сеть квадратов в масштабе М 1:500. Сторону А1–А4 ориентируют на север и принимают за ось абсцисс – Х, а сторону А1–В1 принимают за ось ординат – Y. В каждой вершине квадрата подписывают вычисленные отметки с точностью до 0,01 м. По всем сторонам квадратов и по диагоналям (направлениям скатов местности) выполняют интерполирование горизонталей. 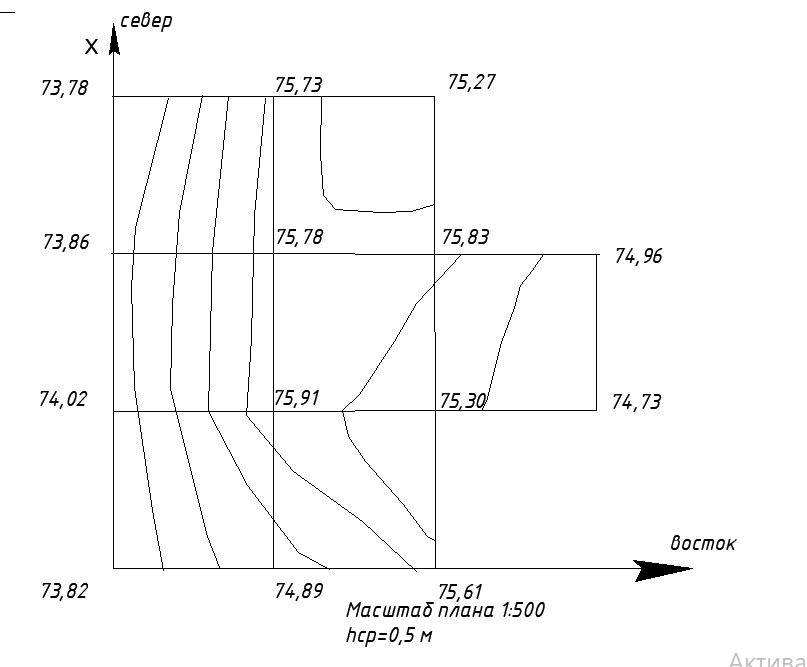 Рис. 1.3. Топографический план строительной площадки. Вычисление проектной отметки горизонтальной площадки. Вычисляют проектную отметку горизонтальной площадки по формуле:
где Нmin – наименьшая из фактических отметок вершин квадратов, n – число квадратов. Для облегчения расчетов вводят в расчетную формулу понятие: условная отметка h. Вычисляют условную отметку для каждой вершины квадрата:
Согласно топографическому плану (рис. 1.3.) вычисляют: h1, h2, h3, h4 h1 – сумма отметок вершин квадратов, принадлежащих только одному квадрату;
h2 – сумма отметок вершин квадратов общих для двух смежных квадратов:
Полученную сумму h2 подставляют в формулу (2.1): h3 – сумма отметок вершин квадратов общих для трех смежных квадратов:
h3 = НВ2 + НВ3. Полученную сумму h3 подставляют в формулу (2.1): h4 – сумма отметок вершин, объединяющих четыре квадрата;
Полученную сумму h4 подставляют в формулу (2.1): В рассматриваемом примере Нmin = 69,60 м. h1 = 73,82 + 73,78+ 75,27 + 74,73+74,96 +75,76=448,31. h2 =75,73 + 74,89 + 74,02+73,86 =298,49. h3= 75,83+ 75,30= 151,13 м; h4= 75,91+ 75,78= 151,69 м. Подставляют все полученные величины в формулу вычисления проектной отметки горизонтальной площадки (2.1): 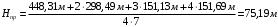 Таким образом, проектная отметка горизонтальной площадки: Нпр.гор = 75,19 м. Вычисление рабочих отметок всех вершин квадратов Вычисляют рабочие отметки всех вершин квадратов, показывающих высоту насыпи (+) или глубину выемки (–) как разность проектной и фактических отметок по формуле:
Например, рабочую отметку вершины А4 вычисляют:
Правильность вычисления рабочих отметок контролируют по формуле:
Вычисление положения точек нулевых работ Вычерчивают картограмму земляных работ. Картограмма земляных работ – это графический документ вертикальной планировки. Составляется на основе топографического плана строительной площадки. Для этого вычерчивают сеть квадратов и в каждой вершине подписывают фактические (черные) отметки и вычисленные рабочие отметки. Проектную отметку подписывают ниже картограммы. 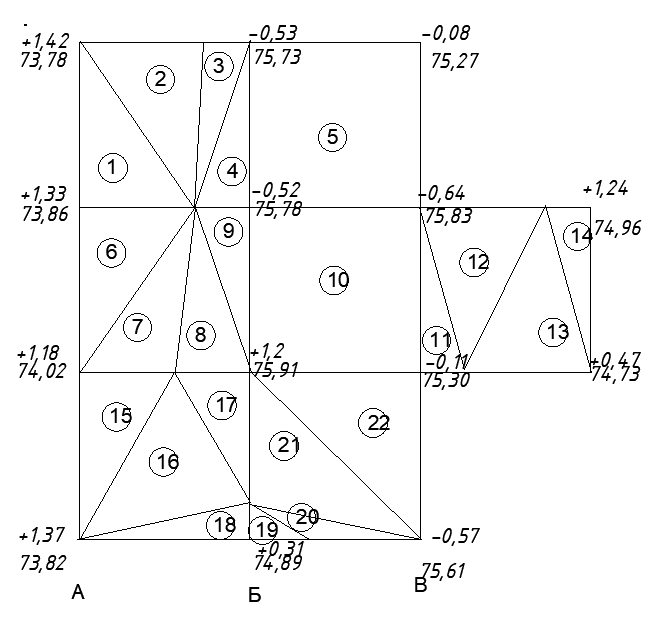 Рис. 2.1. Картограмма земляных работ Нп.р = 75,19 м. Длина сторон квадрата 20 м. Вычисляют положение точек нулевых работ. Ноль работ – это точка пересечения фактической линии (линии Земли) и проектной линии. Определение положения точек нулевых работ проводят между смежными рабочими отметками сторон квадратов, имеющими разные знаки. Положение точек нулевых работ определяют аналитическим способом по формуле:
Контроль вычислений: l1 + l2 = l где h2 – рабочая отметка выемки; h1 – рабочая отметка насыпи; l – длина стороны квадрата; l1 и l2 – расстояния, определяющие положение точек нулевых работ на стороне квадрата (рис. 2.2.). 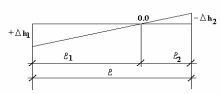 Рис. 2.2. Определение положения точек нулевых работ Пример вычисления точки нулевых работ: Для стороны между вершинами А4–Б4 положение точки нулевых работ определяют:
Точка нулевых работ находится на расстоянии 15 м от вершины квадрата с рабочей отметкой + 1,42 м. Соединив точки нулевых работ прямыми линиями, получают линию нулевых работ. Объем земляных масс можно вычислить методом четырехгранных или трехгранных призм. Объем четырехгранной призмы определяют по формуле:
где 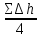 – средняя высота однородной призмы, вычисляют как среднюю арифметическую из рабочих отметок; S – площадь основания призмы.Объем трехгранной призмы определяют по формуле:
Объем пятигранных призм в смешанных квадратах можно вычислять как разность объемов четырехгранных и трехгранных призм. Вычисление объемов земляных масс насыпей и выемок выполняют для каждого квадрата или части его, используя вышеприведенные формулы. После вычисления объемов отдельных фигур находят общий объем насыпи и выемки. Контролем вычисления объемов земляных масс является примерное равенство объемов насыпи и выемки. Допускается расхождение в пределах до 5% от общего объема насыпи и выемки. При этом предпочтительно, чтобы объем выемки несколько превышал объем насыпи, это связано с уплотнением и потерями грунта при его отсыпке в насыпь. Пример вычисления объема земляных масс по данным рис. 2.1. приведен в таблице 2.1. Таблица 2.1 Ведомость вычисления объемов земляных масс
Вычисляют объемы выемок и насыпей:
Определяют абсолютную величину их разности:
Отношение V к общей сумме насыпей и выемок, выраженное в процентах, характеризует баланс земляных масс:
1 2 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
,
,
,
,
.
,
,
.
,
,
.
,
.
,
,
.
,
.
.
,
.
.
,
.
,
.
.
.
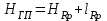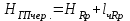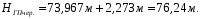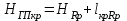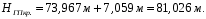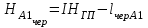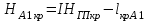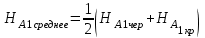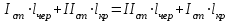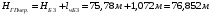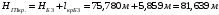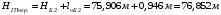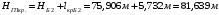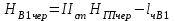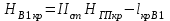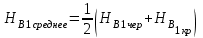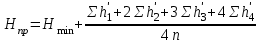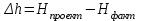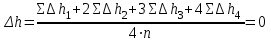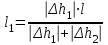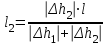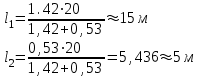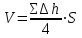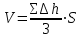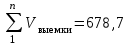
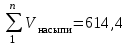
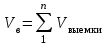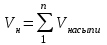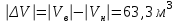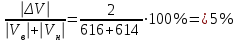