Учёт влияния гибкости внецентренно-сжатых элементов и длительности загружения. Контрольная работа. Контрольная Работа Тема Учёт влияния гибкости внецентренносжатых элементов и длительности загружения
 Скачать 157.5 Kb. Скачать 157.5 Kb.
|
|
Контрольная Работа Тема: Учёт влияния гибкости внецентренно-сжатых элементов и длительности загружения Сжатые и растянутые элементы встречаются как самостоятельные конструкции - колонны, стены, арки, а могут быть элементами более сложных конструкций например ферм. На напряженно-деформированное состояние таких элементов очень сильно влияют, помимо геометрических характеристик сечения и физико-механических свойств материалов, эксцентриситет действующих усилий и гибкость элементов. Эти факторы могут приводить к тому, что сжатый или растянутый элемент фактически начинает работать как изгибаемый, с соответствующей схемой разрушения, что обязательно учитывается при расчете. Технологически такие элементы могут выполняться как в сборном так и в монолитном варианте, с предварительным напряжением или без него, с гибкой или жесткой арматурой. В производство несущих каркасов произошло внедрение высокопрочного бетона, что привело к использованию конструкций из сжатых колонн, так как они обладали меньшими размерами поперечных сечений по сравнению с обычными бетонными секциями. Потери устойчивости возрастает, при увеличении гибкости, а также колонны изначально изгибаются в плоскости эксцентриситета или плоской деформации. Гибкость увеличивается, поэтому возможность потери устойчивости возрастает, когда колонны изначально изгибаются в плоскости эксцентриситета или плоской деформации. Поэтому возрастает важность совершенствования метода проверки колонн. Существует два случая работы внецентренно-сжатых элементов (рис.1). Основное отличие между ними заключается в следующем: в первом случае относительная высота сжатой зоны бетона, меньше граничного значения, сечение сжато частично, когда большая его часть растянута. В этом случае арматура А, растянута, а вторая арматура А' сжата этот случай называют случаем больших эксцентриситетов. Во втором случае большая часть или все сечение колонны сжаты, и тогда при сравнении с первым случаем меняется характер работы арматуры: напряжения в арматуре А, расчетные значения сопротивления арматуры не достигаются, и она может быть либо слабо сжата, либо слабо растянута этот случай называют случай малых эксцентриситетов. 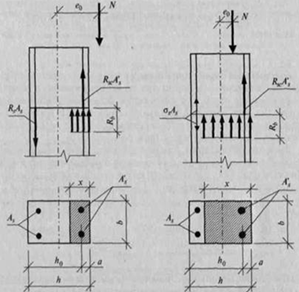 Рис. 1. Два случая работы внецентренно-сжатых элементов Сжатые бетонные элементы очень сложно поддаются центральному сжатию, например, несовершенные геометрические формы колонн, характеристики несущих конструкций, недостаточная точность регулировки арматуры, неоднородность бетона и другие факторы. Приводит это к тому, что практически все сжатые бетонные элементы можно считать сжатыми отдельно. Нагрузка, под которой находится вертикальный стержень (рис. 2), потерянная устойчивость зависит лишь от момента инерции участка I и от модуля Юнга. Данный стержень не разрушается при образовании выпуклости. Он изгибается так, чтобы он "выскользнул" из-под нагружаемой силы. Если "предел упругости" материала не был достигнут во время нагружения, то после снятия нагрузки стержень снова выпрямится. 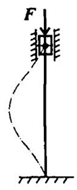 Рис. 2. Действие силы F на стержень Применяемость изобретенного Эйлером математического метода вариационного исчисления при возможности определении наименьшей высоты тонкого вертикального стержня, при которой этот стержень начинает выпучиваться под собственным весом, привело к получению формулы Эйлера. Формула Эйлера применима в некоторых случаях, когда гибкость стержня превосходит или равна предельной гибкости. В тех случаях, когда гибкость стержней меньше предельной, формулу Эйлера нельзя применить и пользуются эмпирической формулой Ясинского. В дальнейшем, множественные исследования Ф.С. Ясинского и других многих ученых показали, что среди упругопластических деформаций формула Эйлера не может быть применима. Именно поэтому использование на практике может быть только в некоторых случаях, когда при гибкостях λ, которые превышают критическую величину λcr, когда связь между напряжениями и деформациями во всех материалах конструкции можно считать пропорциональной. Производится оценивание несущей способности сжатых элементов различной гибкости по условиям прочности и устойчивости, а также для железобетонных колонн, которые были испытаны Бабичем С.В. и Астафьевым Д.О. при гибкостях λ = 93 и λ = 78. Итоги сравнения экспериментальных данных с результатами аналитического расчета, которые были получены по данной методике, показали некоторые малочисленные расхождения, что допускает возможность ее применения при решении поверочных и проектировочных задач. Расчет бетонных и железобетонных конструкций по деформациям должен производиться из условия, по которому прогибы, углы поворота, перемещения и амплитуды колебания конструкций от многочисленных воздействий не должны превышать соответствующих им предельно допустимых значений. Расчет внецентренно сжатых колонн производят с учетом их работы в системе поперечного каркаса здания. Наряду со множеством достоинств большинства разработанных методик, которые могут позволять оценивать напряженное состояние железобетонного элемента во всех стадиях нагружения, также присутствует и недостаток: почти все отмеченные методики были созданы применительно к расчету изгибаемых и внецентренно сжатых железобетонных элементов малой гибкости. В гибких железобетонных вертикальных стержнях, несущая способность которых находится в прямой зависимости от величины деформаций. Для надежного и точного использования различных методик расчета, которые должны учитывать фактические диаграммы деформирования бетона, нужно располагать аналитическими зависимостями между напряжениями и деформациями бетона. Сегодня таких зависимостей большое множество, но все же предпочтение отдается диаграммам, которые отражают реальную работу бетона под нагрузкой, и при этом отличающимися простотой записи и легкостью выполнения операций интегрирования и дифференцирования. Вопрос расчета гибких внецентренно-сжатых элементов исследован весьма глубоко, но все же прямого сопоставления результатов по различным методам не было найдено в доступных источниках. Системное подтверждение расчетных методик на основе испытаний и сопоставление результатов с популярными расчетами по недеформированной схеме представляют очень важную задачу для всей практики проектирования Задача №1, Вариант №4. Определите несущую способность пустотной плиты перекрытия при следующих условиях: 1. Ширина плиты – bп = 1,5 м. 2. Прочность бетона – R b = 100 кг/см2. 3. Прочность арматуры – RS = 3650 кг/см2 4. Высота полки - hп = 3,5 см. 5. Рабочая высота сечения – ho = 20 см. 6. Площадь сечения арматуры As= 10.77 см2. 7. Расчетная длина элемента L= 9 м. 8. Расчётная нагрузка q= 140 кг/м2. Решаем: 1) Мнагр.= b*q*L2/8= 1.5*140*81/8 = 2126.25 кг.м. 2) X= Rs*As/(Rb*bп)= 3650*10,77/(100*150) = 2,62см. 3) Так как, X ˂ 3,5, то Мнес.сп.= As*Rs(ho-As*Rs/(2*Rb*bп)) = 10,77*3650(20-(10,77*3650)/(2*100*150))= 734713= 7,35*105 кг.см2. 4) Мнес.сп.>Мнагр., т.е. 7350 > 2126,25 кг.м., из этого следует, что несущая способность плиты больше приложенной к ней нагрузки. Задача №2, Вариант №4. Рассчитать железобетонный фундамент под колонну сечением 40х40 см. Фундамент принять двухступенчатым, квадратным в плане. Расчетная нагрузка на фундамент с учетом коэффициента надежности по назначению N=1000кН. Коэффициент надежности по нагрузке Yf=1,2. Бетон фундамента класса В12.5. Арматура в фундаменте класса А-I, продольная арматура колонны диаметром 20 мм. Глубина заложения подошвы фундамента Н1. Удельный вес бетона фундамента и грунта на его обрезах Yср=20 кН/м3. Расчётная нагрузка N= 960kH, Глубина заложения подошвы H1= 1,7м., Расчётное сопротивление основания R0=0.16 Мпа. Решаем: Nп= N/Vf = 960/1.2 = 800 kH Расчётное сопротивление бетона классом В12.5, на растяжение при Vы = 0,9: Rы = 0.65 Мпа. Расчётное сопротивление арматуры Rs = 280 Мпа. Требуемая площадь подошвы квадратного фундамента. А= а*а = Nп/Rо-Yср.H1 = 800/200-22*1.7 = 4.92м2 Размер сторон а = √А = √4,92 = 2,21м. Округляя применяем а = 2,2м, А = 2,2² = 4,84м. Реактивный отпор грунта Pгр = N/A = 960/4.84= 198 kHм². Рабочая высота из условий продавливания hо = (hr + br)/U + ½√N/Rbt+Pгр = (0,4+0,4)/4+½*(960+198) = 0,36м. Высота фундамента, с учётом конструктивных требований, из условий заданной колонны h = 1,5 hr+25 = 1,5*40+25 = 85см. Из условий анкеровки продольной арматуры колонны ds = 20мм. в фундаменте h = 30ds+25=30*20+25 = 85см. h = 85см. Рабочая высота фундамента ho = h-4=85- 4= 81см. Предварительно принимаем высоту ступеней h1= 45см; hot = h1-4= 45 – 4 = 41см. h2= 85- 45 = 40 см. а1 = hr + 2h2 = 40+2*40 = 120 см. Проверяем высоту нижней ступени по поперечной силе Ɩ = (a/2 - hr /2 – ho) = 2.2/2 – 0.4/2 – 0.81 = 0.09м. Проверяем условия 198*0,09˂1,5*650*0,41; 17˂400 kH Определяем изгибающий момент в сечении I и II при b=a. M1 = 0.125*Pгр(а-ha)² b = 0.125*198(2.2-0.4)²*2.2 = 176.41 kH/м Мп = 0,125*Pгр(a-a1)² b = 0.125*198(2.2-1.2)²*2.2 = 54.45 kH/м Площадь сечения арматуры Ast = M1/(0,9*hr0Rs) = 5445/(0.9*81*28) = 8.62 см² Ask = M11/(0.9*hr1*Rs) = 5445/(0.9*41*28) = 5.26 см² M = As*100/(b*h0) =(12.44*100)/220*81 = 0.7>μ=0.01% |
