Численные методы. Контрольная работа Вариант 12 Задание 1
 Скачать 37.81 Kb. Скачать 37.81 Kb.
|
|
Контрольная работа Вариант 12 Задание 1. Дано приближенное число x=3,7368 и его абсолютная погрешность ∆x=0,01807. Определить предельную относительную погрешность и какие значащие цифры приближенного числа будут верными в широком (узком) смысле. Решение Воспользуемся формулой (2.6’). Тогда предельная относительная погрешность равна: 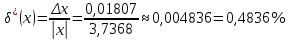 Для определения значащих цифр приближенного числа х в широком (и узком) смысле воспользуемся формулами (3.2) и (3.3). Запишем приближенное число 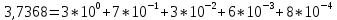 , где m = 0 – старший десятичный разряд числа. , где m = 0 – старший десятичный разряд числа.Количество верных значащих цифр n приближенного числа в широком смысле (ω = 1) определятся неравенством (3.3): 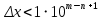 В нашем случае: 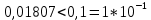 Таким образом: 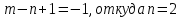 Следовательно, в приближенном числе x = 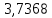 верными значащими цифрами в широком смысле являются 3 и 7. верными значащими цифрами в широком смысле являются 3 и 7.Количество верных значащих цифр числа в узком смысле (ω = 0,5) определятся неравенством (3.2): 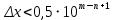 В нашем случае: 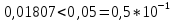 Таким образом: 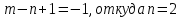 Следовательно, в приближенном числе x= 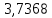 верными значащими цифрами в узком смысле являются 3 и 7. верными значащими цифрами в узком смысле являются 3 и 7.Задание 2. Дано приближенное число x = 0,038365 и его относительная погрешность 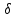 =5,0%. Определить предельную абсолютную погрешность и какие значащие цифры приближенного числа будут верными в широком (узком) смысле. =5,0%. Определить предельную абсолютную погрешность и какие значащие цифры приближенного числа будут верными в широком (узком) смысле.Решение Из формулы (2.6’) предельная абсолютная погрешность равна: 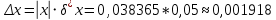 Запишем приближенное число 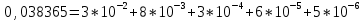 , где m = -2– старший десятичный разряд числа. , где m = -2– старший десятичный разряд числа.Количество верных значащих цифр n приближенного числа в широком смысле (ω = 1) определятся неравенством (3.3): 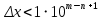 В нашем случае 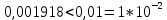 Таким образом: 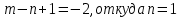 Следовательно, в приближенном числе x = 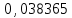 верной значащей цифрой в широком смысле является 3. верной значащей цифрой в широком смысле является 3.Количество верных значащих цифр числа в узком смысле (ω = 0,5) определятся неравенством (3.2): 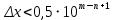 В нашем случае: 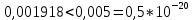 Таким образом: 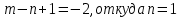 Следовательно, в приближенном числе x = 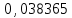 верной значащей цифрой в узком смысле является 3. верной значащей цифрой в узком смысле является 3.Задание 3. Дано приближенное число x = 135,16883 и известно, что у этого числа n = 4 верных значащих цифры в широком (узком) смысле. Оценить абсолютную и относительную погрешности в обоих случаях. Определить предельную абсолютную и относительную погрешности в обоих случаях. Решение Запишем приближенное число 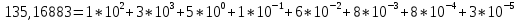 , где m = 2 – старший десятичный разряд числа. , где m = 2 – старший десятичный разряд числа.Согласно неравенству (3.3) оценим абсолютную погрешность числа в случае ω = 1: 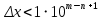 = =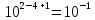 Таким образом, абсолютная погрешность ∆х = 0,1. При этом относительная погрешность равна: 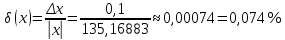 Согласно неравенству (3.2) оценим абсолютную погрешность числа в случае ω = 0,5: 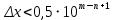 = =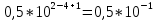 Таким образом, абсолютная погрешность ∆х = 0,05. При этом относительная погрешность равна: 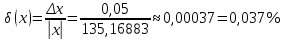 Предельную относительную погрешность оценим по формуле (5.4): 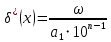 где 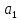 0 – первая значащая цифра числа (в данном примере 0 – первая значащая цифра числа (в данном примере 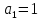 ). ).Имеем При ω = 1: 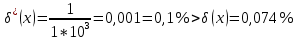 При ω = 0,5: 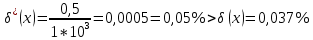 Предельную абсолютную погрешность оценим из формулы (2.6’): При ω = 1: 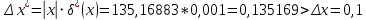 При ω = 0,5: 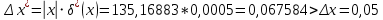 Задание 4. Определить, какое равенство точнее: 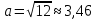 или или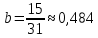 ? ?Решение Для нахождения предельных абсолютных погрешностей берем числа a и b с большим числом десятичных знаков: 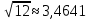 ; ; 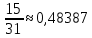 . Определяем предельные абсолютные погрешности, округляя их с избытком: . Определяем предельные абсолютные погрешности, округляя их с избытком: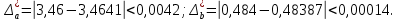 Находим предельные относительные погрешности: 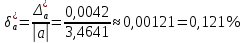 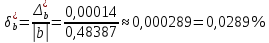 Второе равенство является более точным, поскольку 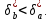 Задание 5. Дана функция 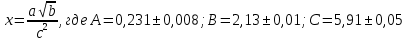 . Запишите порядок выполняемых вами операций, оцените погрешности их результатов, вычислите и оцените погрешность искомого значения. Определить число верных знаков в результате. . Запишите порядок выполняемых вами операций, оцените погрешности их результатов, вычислите и оцените погрешность искомого значения. Определить число верных знаков в результате.Решение Произведем вычисление функции в порядке, определяемом приоритетом математических действий, а также оценим погрешность выполняемых операций. 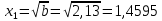 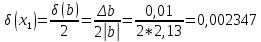 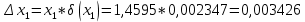 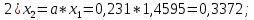 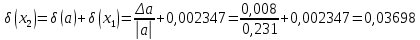 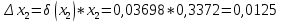 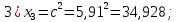 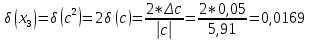 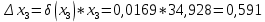 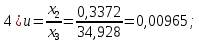 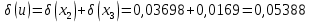 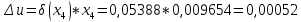 Оценим погрешность искомой функции u и определим число верных значащих цифр. Запишем 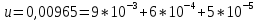 , где m =-3 – старший десятичный разряд числа. , где m =-3 – старший десятичный разряд числа.Имеем: в широком смысле (ω = 1): 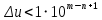 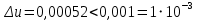 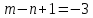 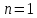 Таким образом, верной значащей цифрой числа u является цифра 9. Запишем число u с учетом правил округления (п. 1.4 методических указаний), сохранив только разряды с верными значащими числами, т.е. u = 0,010. При этом погрешность округления составит: 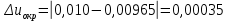 Тогда, абсолютная погрешность округленного значения функции u равна: 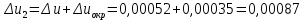 Для 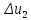 условие (3.3) меняется: условие (3.3) меняется: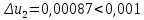 следовательно, число верных цифр уменьшается на 1 цифру. Таким образом, окончательный ответ для функции u имеет вид: u = 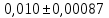 . . |
