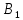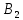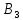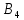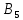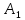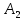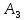мет оптим реш. Решение. Контрольная работа вариант 2 задание 1 Составить экономикоматематическую модель задачи и решить ее графическим методом
 Скачать 124.91 Kb. Скачать 124.91 Kb.
|
|
КОНТРОЛЬНАЯ РАБОТА ВАРИАНТ № 2 ЗАДАНИЕ 1 Составить экономико-математическую модель задачи и решить ее графическим методом. На звероферме могут выращиваться черно-бурые лисицы и песцы. Для обеспечения нормальных условий их выращивания используется 3 вида кормов. Количество корма каждого вида, которое должны ежедневно получать лисицы и песцы приведено в таблице. В ней же указаны общее количество корма каждого вида, которое может быть использовано зверофермой, и прибыль от реализации одной шкурки лисицы и песца.
Определить, сколько лисиц и песцов следует выращивать на звероферме, чтобы прибыль от реализации их шкурок была максимальной. Решение: Математическая модель задачи Пусть 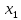 – количество чернобурых лисиц – количество чернобурых лисиц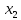 – количество песцов – количество песцов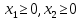 Ограничение на корм вида I: 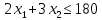 Ограничение на корм вида II: 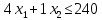 Ограничение на корм вида III: 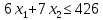 Целевая функция - прибыль от реализации одной шкурки: 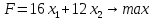 Получили математическую модель задачи: 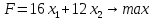 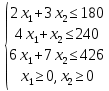 По итогу решения ЗЛП будет сделан экономический вывод: какой должен быть план развода животных для получении максимальной прибыли, и сколько при этом будет затрачено ресурсов. Графическое решение задачи линейного программирования: Рассмотрим неравенство 1 системы ограничений. 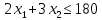 Построим прямую: 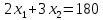 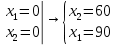 Нашли координаты двух точек (0, 60) и (90, 0). Соединяем их и получаем необходимую прямую (1). 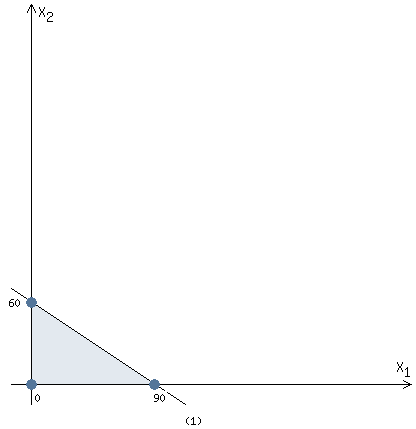 Рассмотрим неравенство 2 системы ограничений. 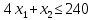 Построим прямую: 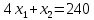 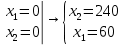 Нашли координаты двух точек (0, 240) и (60, 0). Соединяем их и получаем необходимую прямую (2). 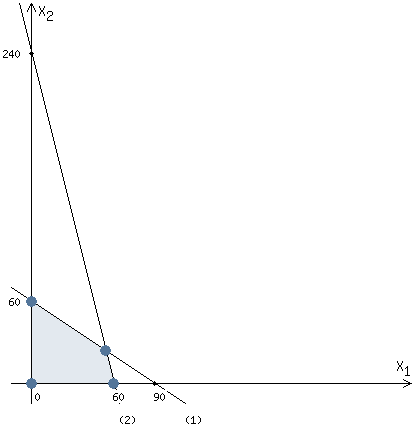 Рассмотрим неравенство 3 системы ограничений. 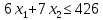 Построим прямую: 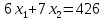 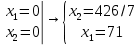 Нашли координаты двух точек (0, 426/7) и (71, 0). Соединяем их и получаем необходимую прямую (3). Строим вектор 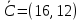 , координатами которого являются коэффициенты функции , координатами которого являются коэффициенты функции 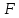 . .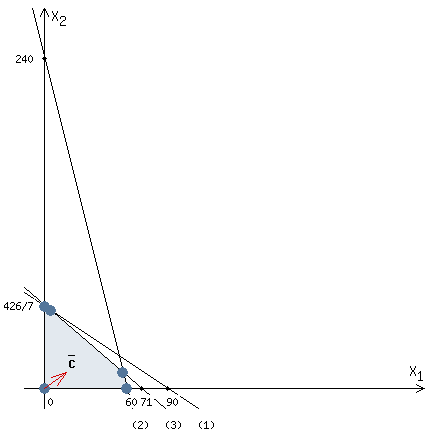 Перемещаем красную прямую, перпендикулярно вектору 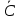 , от левого нижнего угла к правому верхнему. , от левого нижнего угла к правому верхнему.В точке, в которой красная прямая в последний раз пересечет область допустимых решений, функция 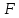 достигает своего наибольшего значения. достигает своего наибольшего значения.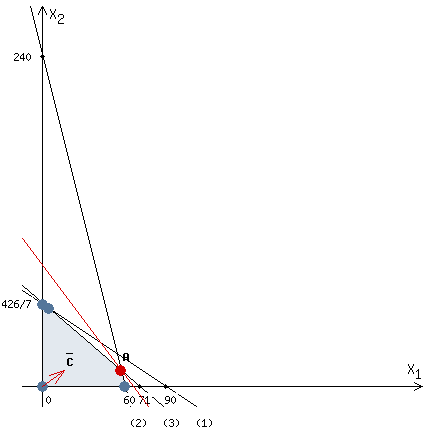 Таким образом, функция 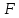 достигает наибольшего значения в точке достигает наибольшего значения в точке 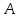 . Найдем координаты точки . Найдем координаты точки 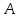 . .Точка 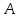 одновременно принадлежит прямым (2) и (3). одновременно принадлежит прямым (2) и (3).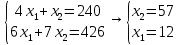 Вычислим значение функции 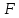 в точке в точке 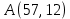 . .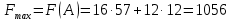 Экономический вывод: Для получения максимальной прибыли в размере 1056 ден. ед. план развода животных должен быть таким: лисиц - 57 единиц, песец - 12 единиц. При этом, затраты ресурсов составят: "Корм I" - 150 единицы при запасе 180 ед. (остаток 30 единиц); "Корм II" - 240 кг единицы при запасе 240 ед.; "Корм III" - 426 единиц при запасе 426 ед. Избыточным является ресурс "Корм I", недостаточным - "Корм II" и "Корм III". ЗАДАНИЕ 2 Решить транспортную задачу распределительным методом или методом потенциалов. Имеются три пункта-поставщика однородного груза 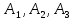 и пять пунктов и пять пунктов 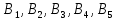 потребления этого груза. На пунктах потребления этого груза. На пунктах 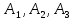 находится груз соответственно в количестве находится груз соответственно в количестве 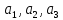 тонн. В пункты тонн. В пункты 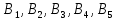 требуется доставить соответственно требуется доставить соответственно 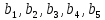 тонн груза. Стоимость перевозки одной единицы груза от поставщиков к потребителям приведена в следующей таблице: тонн груза. Стоимость перевозки одной единицы груза от поставщиков к потребителям приведена в следующей таблице:
Найти такой план закрепления потребителей за поставщиками, чтобы затраты по перевозкам всех грузов были минимальными. Решение: Проверим выполнение условия: суммарные запасы продукции у поставщиков должны равняться суммарной потребности потребителей. Запасы поставщиков: 70+80+150=300 единиц продукции Потребность потребителей: 20+70+30+80+100=300 единиц продукции. Условие выполнено. Перейдем к решению транспортной задачи Во-первых, задействуем маршруты с наименьшей стоимостью доставки.
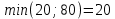
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||