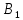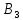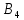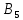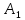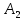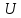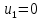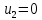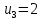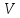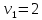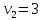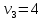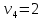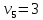мет оптим реш. Решение. Контрольная работа вариант 2 задание 1 Составить экономикоматематическую модель задачи и решить ее графическим методом
 Скачать 124.91 Kb. Скачать 124.91 Kb.
|
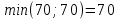 Ситуация, в которой нужно исключить поставщика 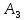 и потребителя и потребителя 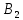 одновременно. Исключим только потребителя одновременно. Исключим только потребителя 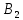 . Запас поставщика . Запас поставщика 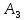 будет считаться равным 0. будет считаться равным 0.
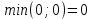 Так как в ячейке находится 0, то маршрут считается задействованным
Стоимость доставки продукции для начального решения 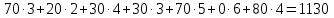 ден. ед. ден. ед.Проверим на оптимальность. Применим метод потенциалов Каждому поставщику 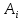 ставим в соответствие некоторое число ставим в соответствие некоторое число 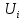 - потенциал поставщика. - потенциал поставщика.Каждому потребителю 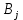 ставим в соответствие некоторое число ставим в соответствие некоторое число 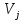 - потенциал потребителя. - потенциал потребителя.Для задействованного маршрута: потенциал поставщика + потенциал потребителя = тариф задействованного маршрута. Последовательно найдем значения потенциалов. Значение одного потенциала необходимо задать. Пусть u2 = 0. A2B1 : v1 + u2 = 2 v1 = 2 - 0 = 2 A2B3 : v3 + u2 = 4 v3 = 4 - 0 = 4 A2B5 : v5 + u2 = 3 v5 = 3 - 0 = 3 A3B3 : v3 + u3 = 6 u3 = 6 - 4 = 2 A3B4 : v4 + u3 = 4 v4 = 4 - 2 = 2 A1B5 : v5 + u1 = 3 u1 = 3 - 3 = 0 A3B2 : v2 + u3 = 5 v2 = 5 - 2 = 3
Оценки незадействованных маршрутов (cij - стоимость доставки). A1B1 : Δ11 = c11 - ( u1 + v1 ) = 3 - ( 0 + 2 ) = 1 A1B2 : Δ12 = c12 - ( u1 + v2 ) = 5 - ( 0 + 3 ) = 2 A1B3 : Δ13 = c13 - ( u1 + v3 ) = 8 - ( 0 + 4 ) = 4 A1B4 : Δ14 = c14 - ( u1 + v4 ) = 6 - ( 0 + 2 ) = 4 A2B2 : Δ22 = c22 - ( u2 + v2 ) = 5 - ( 0 + 3 ) = 2 A2B4 : Δ24 = c24 - ( u2 + v4 ) = 7 - ( 0 + 2 ) = 5 A3B1 : Δ31 = c31 - ( u3 + v1 ) = 7 - ( 2 + 2 ) = 3 A3B5 : Δ35 = c35 - ( u3 + v5 ) = 8 - ( 2 + 3 ) = 3 Нет отрицательных оценок. Следовательно, уменьшить общую стоимость доставки продукции невозможно. Ответ: 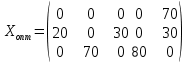 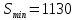 ден. ед. ден. ед. ЗАДАНИЕ 3 Полезность набора двух товаров выражается функцией 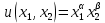 , где , где 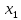 и и 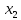 – количества товаров. Единица первого товара стоит – количества товаров. Единица первого товара стоит 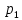 , единица второго товара стоит , единица второго товара стоит 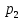 . Потребитель может истратить на эти товары до . Потребитель может истратить на эти товары до 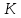 денежных единиц. Каковы оптимальные значения и для максимальной полезности набора? Решить задачу двумя способами: денежных единиц. Каковы оптимальные значения и для максимальной полезности набора? Решить задачу двумя способами: 1) через равенство угловых коэффициентов кривой безразличия и бюджетной прямой; 2) методом множителей Лагранжа. Решение: Модель задачи 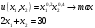 1) через равенство угловых коэффициентов кривой безразличия и бюджетной прямой. уравнение бюджетной прямой 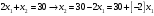 угловой коэффициент = -2 уравнение кривой безразличия 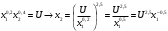 угловой коэффициент (первая производная) 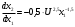 откуда: 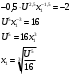 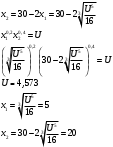 2) методом множителей Лагранжа 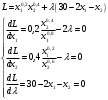 решаем систему 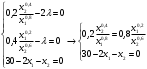 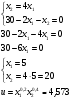 Оба метода дают одинаковое решение задачи: 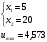 Оптимум потребителя: потребление 5 ед. первого товара и 20 ед. второго товара, при этом максимальная полезность 4,573 ютиля. Проверим существенность бюджетного ограничения, для чего подставляем значения переменных: 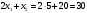 ограничение выполняется строго, то есть имеющийся бюджет расходуется полностью (все 30 ед.) Уравнение кривой безразличия 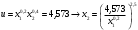 Уравнение линии бюджетной полезности 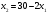 Графики кривой безразличия и линии бюджетной полезности 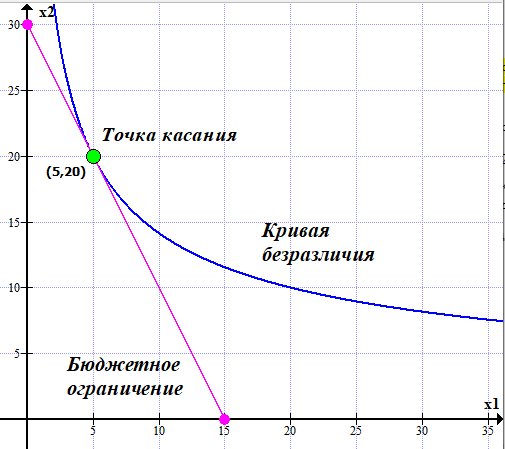 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||