Теория игр лабораторная. Контрольная работа вариант 27 Задание 1
 Скачать 62.69 Kb.
|
|
КОНТРОЛЬНАЯ РАБОТА Вариант 27  Задание №1
Пусть игрок А выбрал стратегию Аi, тогда в наихудшем случае его выигрыш составит:  Игрок А должен выбрать такую стратегию, чтобы максимизировать свой минимальный выигрыш от каждой стратегии αi.  α – максимин, нижняя цена игры Игрок В ищет такую стратегию, при которой его проигрыш будет наименьшим:  β – минимакс, верхняя цена игры Ответ: Игрок А должен выбрать стратегию А1, игроку В целесообразно выбрать стратегию В3. Тогда гарантированный выигрыш игрока А будет равен 50 тыс.руб. Задание №2 Стратегии игроков: Аi – фирма А выбрала выпускать (А1) или не выпускать (А2) новый вид продукции, Bi – фирма B выбрала выпускать (В1) или не выпускать (В2) новый вид продукции. Платежная матрица имеет вид: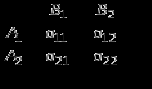 
 p(A1) = p1 = (0-2)/(-8+0-2-17) = 2/27 = 0,07  p(A2) = p2 = 25/27 = 0,93  p(B1) = q1 = (0-17) / (-8+0-2-17) = 17/27 = 0,63  p(B2) = q2 = 10/27 = 0,37 Цена игры:  = ((-8)*0-17*2)/(-8+0-2-17) = 34/27 = 1,26 млн.руб. Ответ: Организации А следует решиться на выпуск нового товара, чтобы полученная ожидаемая прибыль была максимальна, с вероятностью 0,07. Оптимальная смешанная стратегия организации А: P = (0,07; 0,93). Оптимальная смешанная стратегия организации В: Р = (0,63; 0,37). Прибыль при соблюдении организациями оптимальных стратегий составит 1,26 млн.руб. Задание №3
Н 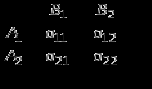аходим доминирующие строки и доминирующие столбцы и удаляем, соответственно, строку А1 (доминирует строка А3), столбец В3 (доминирует столбец В2) и столбец В4 (доминирует столбец В2). Получаем платежную матрицу:
α =max{4, 3}=4 – нижняя цена игры β=min{7, 5}=5 – верхняя цена игры Игра не имеет седловой точки. Вероятности чистых стратегий компании А равны: р(А2) = р2 = (3-7)/(4+3-7-5) = 4/5 = 0,8 р(А3) = р3 = 1-0,8 = 0,2 Цена игры равна: = (4*3-5*7)/(4+3-7-5) = 23/5 = 4,6 Если один из игроков применяет свою оптимальную смешанную стратегию, то его выигрыш равен значению игры v вне зависимости от того, с какими вероятностями будет применять второй игрок стратегии, вошедшие в оптимальную (в том числе и чистые стратегии). Ответ: Следовательно, доля выпуска модели одежды А2 должна составлять 0,8, а модели А3 – должна составлять 0,2. Модель А1 выпускать не рационально. При этом прибыль, не зависимо от действий компании В будет составлять 4,6 у.е. Задание №4
Прямая и двойственная задачи линейного программирования имеют вид: 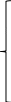 х1+х2+х3+х4minx1+x2+x3+2x41 3x1+3x2+8x3+6x41 x1+5x2+4x3+8x41 4x1+8x2+6x3+3x41 7x1+5x2+5x3+7x41 6x1+7x2+6x3+4x41  xi0, i=1,2,3,4y1+y2+y3+y4+y5+y6max y1+3y2+y3+4y4+7y5+6y61 y1+3у2+5у3+8у4+5у5+7у61 у1+8у2+4у3+6у4+5у5+6у61 2у1+6у2+8у3+3у4+7у5+4у61 уj0, j=1,2,3,4,5,6 α = 2 – нижняя цена игры β= 2 – верхняя цена игры Цена игры равна верхней и нижней цены игры и составляет 2 у.е.. Ответ: Игрок А должен выбрать стратегию А4, игроку В целесообразно выбрать стратегию В1. Тогда гарантированный выигрыш игрока А будет равен 2 у.е. Задание №5
Критерий Лапласа Определим величину среднего выигрыша для каждой из стратегий. qi = 1/n = ¼ ᾱ1 = 161*(1/4)+198*(1/4)+171*(1/4)+201*(1/4) = 182,75 ᾱ2 = 198*(1/4)+187*(1/4)+199*(1/4)+204*(1/4) = 197 ᾱ3 = 204*(1/4)+197*(1/4)+207*(1/4)+187*(1/4) = 198,75 ᾱ4 = 164*(1/4)+164*(1/4)+205*(1/4)+179*(1/4) = 178 ᾱ5 = 206*(1/4)+161*(1/4)+190*(1/4)+188*(1/4) = 186,25 Максимальное значение среднего выигрыша соответствует стратегии Cи равно 198,75. Составим матрицу рисков: 1-й столбец матрицы рисков: r11 = 206 - 161 = 45; r21 = 206 - 198 = 8; r31 = 206 - 204 = 2; r41 = 206 - 164 = 42; r51 = 206 - 206 = 0; 2-й столбец матрицы рисков: r12 = 198 - 198 = 0; r22 = 198 - 187 = 11; r32 = 198 - 197 = 1; r42 = 198 - 164 = 34; r52 = 198 - 161 = 37; 3-й столбец матрицы рисков: r13 = 207 - 171 = 36; r23 = 207 - 199 = 8; r33 = 207 - 207 = 0; r43 = 207 - 205 = 2; r53 = 207 - 190 = 17; 4-й столбец матрицы рисков: r14 = 204 - 201 = 3; r24 = 204 - 204 = 0; r34 = 204 - 187 = 17; r44 = 204 - 179 = 25; r54 = 204 - 188 = 16
Определим величину среднего риска для каждой из стратегий: ȓ1 = 45*(1/4)+36*(1/4)+3*(1/4) = 21 ȓ2 = 8*(1/4)+11*(1/4)+8*(1/4) = 6,75 ȓ3 = 2*(1/4)+1*(1/4)+17*(1/4) = 5 ȓ4 = 42*(1/4)+34*(1/4)+2*(1/4)+25*(1/4) = 25,75 ȓ5 = 37*(1/4)+17*(1/4)+16*(1/4) = 17,5 Минимальное среднее значение риска соответствует стратеги C и равно 5. Ответ: Игроку следует выбрать стратегию С. Критерий Вальда
Ответ: Поскольку минимальные значения выигрышей одинаковы, то согласно критерию Вальда, игрок может выбрать любую из двух стратегий B и C. Метод максимального оптимизма.
Ответ: Игроку следует выбрать стратегию С. Критерий Сэвиджа. Матрица рисков:
Ответ: В соответствии с критерием Сэвиджа, оптимальной будет стратегия В. Критерий Гурвица Пусть λ=0,4, тогда у = max {(0.4*161+(1-0.4)*201);( 0.4*187+(1-0.4)*204);(0.4*187+(1-0.4)*207);(0.4*164+(1-0.4)*205);(0.4*161+(1-0.4)*206)} = max {185; 197.2; 199; 188.6; 188} = 199 Ответ: Полученное значение соответствует стратегии С, которая в силу критерия Гурвица будет признана оптимальной. Вывод: Итак, для данной игры, стратегия С была признана оптимальной в 4-х случаях из 5 (критерий Лапласа, метод максимального оптимизма, критерии Вальда и Гурвица), а вторая стратегия В была предпочтительнее в 2-х случаях (критерии Сэвиджа и Вальда). Значит стратегия С – оптимальная. Задание №6.
Критерий Лапласа. Определим величину среднего выигрыша для каждой из стратегий. qi = 1/n = 1/5 ᾱ1 = 1/5*(27+33+23+7+29) = 23,8 ᾱ2 = 1/5*(31+11+22+31+21) = 23,2 ᾱ3 = 1/5*(31+32+16+13+30) = 24,4 ᾱ4 = 1/5*(8+18+32+33+16) = 21,4 Минимальное значение среднего выигрыша соответствует стратегии Dи равно 21,4. Составим матрицу рисков:
Определим величину среднего риска для каждой из стратегий: ȓ1 = 12,2 ȓ2 = 11,6 ȓ3 = 12,8 ȓ4 = 9,8 Минимальное среднее значение риска соответствует стратеги D и равно 9,8. Ответ: Игроку следует выбрать стратегию D. Критерий Вальда
Ответ: Согласно критерию Вальда, игрок должен выбрать стратегию B. Метод максимального оптимизма.
Ответ: Согласно методу максимального оптимизма, игрок должен выбрать стратегию А. Критерий Сэвиджа. Матрица рисков:
Ответ: Игроку следует выбрать стратегию A. Критерий Гурвица. Пусть λ=0,6, тогда
y = min {17,4;19;20,6;18} = 17,4 Ответ: Полученное значение соответствует стратегии A, которая в силу критерия Гурвица будет признана оптимальной. Вывод: Итак, для данной игры, стратегия А была признана оптимальной в 3-х случаях из 5 (метод максимального оптимизма, критерии Сэвиджа и Гурвица), вторая стратегия В была предпочтительнее в 1 случае (критерий Вальда), стратегия D была признана оптимальной в 1 случае (критерий Лапласа). Значит стратегия А – оптимальная. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Bj 
Bj 
Bj