Тесты по исследованию операции. Исследование операций
 Скачать 219.97 Kb. Скачать 219.97 Kb.
|
|
Вариант 1 1. Термин "исследование операций” появился … в годы второй мировой войны в 50-ые годы XX века в 60-ые годы XX века в 70-ые годы XX века в 90-ые годы XX века в начале XXI века 2. Пусть - нижняя цена, а - верхняя цена парной игры с нулевой суммой. Тогда верно утверждение… 2 + 2 = 1 + = 0 3. Пусть - нижняя цена, а - верхняя цена парной игры с нулевой суммой. Если = = v, то число v называется … ценой игры точкой равновесия оптимальной стратегией смешанной стратегией 4. Пусть - нижняя цена, а - верхняя цена парной игры с нулевой суммой. Если = , то игра называется… игрой с седловой точкой неразрешимым конфликтом игрой без правил 5. Решение называют оптимальным, если оно … по тем или иным признакам предпочтительнее других рационально согласовано с начальством оно утверждено общим собранием 6. Математическое программирование … занимается изучением экстремальных задач и разработкой методов их решения представляет собой процесс создания программ для компьютера под руководством математиков занимается решением математических задач на компьютере 7. Задача линейного программирования состоит в … отыскании наибольшего (наименьшего) значения линейной функции при наличии линейных ограничений создании линейной программы на избранном языке программирования, предназначенной для решения поставленной задачи описании линейного алгоритма решения заданной задачи 8. В задаче квадратичного программирования… целевая функция является квадратичной область допустимых решения является квадратом ограничения содержат квадратичные функции 9. В задачах целочисленного программирования… неизвестные могут принимать только целочисленные значения целевая функция должна обязательно принять целое значение, а неизвестные могут быть любыми целевой функцией является числовая константа 10. В задачах параметрического программирования… целевая функция и/или система ограничений содержит параметр(ы) область допустимых решения является параллелограммом или параллелепипедом количество переменных может быть только четным 11. В двух пунктах А1 и А2 имеется соответственно 60 и 160 единиц товара. Весь товар нужно перевезти в пункты В1, В2, В3 в количестве 80, 70 и 70 единиц соответственно. Матрица тарифов такова: 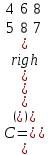 . Спланируйте перевозки так, чтобы их стоимость была минимальной. . Спланируйте перевозки так, чтобы их стоимость была минимальной.Целевой функцией данной задачи является функция: F=4x11+6x12+8x13+5x21+8x22+7x23→min F= 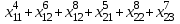 →min →minF=60x1+160x2+80x3+70x4+705 →max F=60x1+160x2–80x3–70x4–705 →min 12. В двух пунктах А1 и А2 имеется соответственно 60 и 160 единиц товара. Весь товар нужно перевезти в пункты В1, В2, В3 в количестве 80, 70 и 70 единиц соответственно. Матрица тарифов такова: 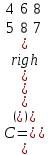 . Спланируйте перевозки так, чтобы их стоимость была минимальной. . Спланируйте перевозки так, чтобы их стоимость была минимальной.Оптимальным планом данной задачи является план: 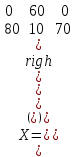 ; ;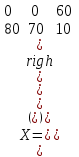 . .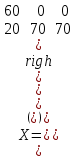 ; ;13. Транспортная задача
будет закрытой, если… a=60, b=80 a=60, b=85 a=60, b=70 a=60, b=75 14. Транспортная задача
является… открытой закрытой неразрешимой 15. Транспортная задача
является… закрытой открытой неразрешимой 16. Для решения следующей транспортной задачи
необходимо ввести… фиктивного потребителя фиктивного поставщика; эффективный тариф эффективную процентную ставку. 17. Для решения следующей транспортной задачи
необходимо ввести… фиктивного поставщика; фиктивного потребителя эффективный тариф эффективную процентную ставку. 18. Среди данных транспортных задач  закрытыми являются… 2 2 и 3 1 и 3 1 19. Исходный опорный план транспортной задачи можно составить … всеми перечисленными методами методом северо-западного угла методом минимального тарифа методом двойного предпочтения методом аппроксимации Фогеля 20. Если целевая функция задачи линейного программирования задана на максимум, то… целевая функция двойственной задачи задается на минимум целевая функция в двойственной задаче отсутствует двойственная задача не имеет решений двойственная задача имеет бесконечно много решений Вариант 2 1. В задачах динамического программирования… процесс нахождения решения является многоэтапным необходимо рационализировать производство динамита требуется оптимизировать использование динамиков 2. Поставлена следующая задача линейного программирования: F(х1, х2) = 5х1 + 6х2→ mах 0.2х1 + 0.3х2 ≤ 1.8, 0.2х1 + 0.1х2 ≤ 1.2, 0.3х1 + 0.3х2 ≤ 2.4, х1 ≥ 0, х2 ≥ 0. Выберите задачу, которая эквивалентна этой задаче. F(х1, х2)= 5х1 + 6х2 → mах, 2х1 + 3х2 ≤ 18, 2х1 + х2 ≤ 12, х1 + х2 ≤ 8, х1 ≥ 0, х2 ≥ 0. F(х1, х2)= 6х1 + 5х2 → min, 2х1 + 3х2 ≤ 18, 2х1 + х2 ≤ 12, х1 + х2 ≤ 8, х1 ≥ 0, х2 ≥ 0. F(х1, х2)= 50х1 + 60х2 → mах, 2х1 + 3х2 ≤ 18, 2х1 + х2 ≤ 12, х1 + х2 ≤ 8, х1 ≥ 0, х2 ≥ 0. F(х1, х2)= 5х12 + 6х22 → mах, 2х1 + 3х2 ≤ 18, 2х1 + х2 ≤ 12, 3х1 + х2 ≤ 2.4, х1 ≥ 0, х2 ≥ 0. 3. Целевой функцией задачи линейного программирования может являться функция: F=12x1+20x2–30x3 →min F= 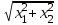 →min →minF= 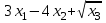 →max →maxF= 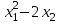 →max. →max.4. Системой ограничений задачи линейного программирования может являться система: 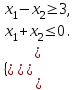 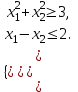 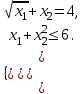 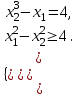 5. Симплекс-метод - это: аналитический метод решения основной задачи линейного программирования метод отыскания области допустимых решений задачи линейного программирования; графический метод решения основной задачи линейного программирования; метод приведения общей задачи линейного программирования к каноническому виду. 6. Задача линейного программирования состоит в: отыскании наибольшего или наименьшего значения линейной функции при наличии линейных ограничений разработке линейного алгоритма и реализации его на компьютере составлении и решении системы линейных уравнений поиске линейной траектории развития процесса, описываемого заданной системой ограничений. 7. Нижняя цена матричной игры, заданной платежной матрицей 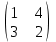 , равна… , равна…2 4 1 3 8. Верхняя цена матричной игры, заданной платежной матрицей 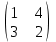 , равна… , равна…3 4 1 2 9. Матричная игра, заданная платежной матрицей 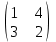 , … , …не имеет седловой точки имеет седловую точку не является парной 10. Область допустимых решений задачи линейного программирования имеет вид: 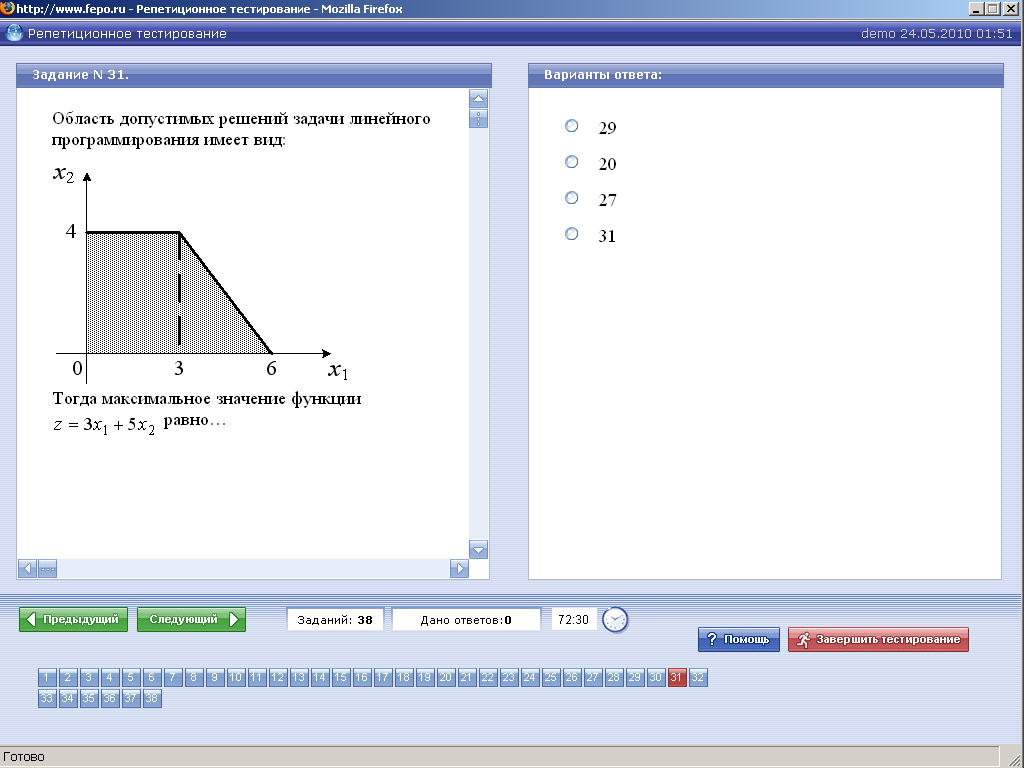 Тогда максимальное значение функции F(х1, х2)= 3х1 + 5х2 равно… 29 20 27 31 11. Если одна из пары двойственных задач имеет оптимальный план, то… и другая имеет оптимальный план другая не имеет оптимального плана другая не имеет допустимых решений 12. Если одна из пары двойственных задач имеет оптимальный план, то… и другая имеет оптимальный план и значения целевых функций при их оптимальных планах равны между собой и другая имеет оптимальный план, но значения целевых функций при их оптимальных планах не равны между собой другая задача может не иметь оптимального плана, но иметь допустимые решения 13. Если целевая функция одной из пары двойственных задач не ограничена (для задачи на максимум – сверху, для задачи на минимум - снизу), то другая задача не имеет допустимых планов другая задача имеет допустимые планы, но не имеет оптимального плана целевая функция другой задачи также не ограничена 14. При решении некоторых задач нелинейного программирования применяется … метод множителей Лагранжа метод Гаусса метод аппроксимации Фогеля метод Гомори 15. Задана задача нелинейного программирования F(х1, х2)= х12 + х22 → mах, х1 + х2 =6, х1 ≥ 0, х2 ≥ 0. Наибольшее значение целевой функции F(х1, х2) … равно 36 равно 18 равно 72 не достижимо (+ ) 16. Задана задача нелинейного программирования F(х1, х2)= х12 + х22 → min, х1 + х2 =6, х1 ≥ 0, х2 ≥ 0. Наименьшее значение целевой функции F(х1, х2) … равно 18 равно 36 равно 6 равно 9 17. Задана задача нелинейного программирования F(х1, х2)= х12 + х22 → mах, х1 + х2 =6, х1, х2 - любые. Наибольшее значение целевой функции F(х1, х2) … не достижимо (+ ) равно 36 равно 18 равно 72 18. Задана задача нелинейного программирования F(х1, х2)= х12 + х22 → min, х1 + х2 =6, х1, х2 - любые. Наименьшее значение целевой функции F(х1, х2) … равно 18 равно 36 равно 6 равно 9 равно 0 не достижимо (- ) 19. Область допустимых решений задачи нелинейного программирования имеет вид:  Тогда максимальное значение функции F(х1, х2)= х12 +х22 равно… 36 72 25 12 20. Область допустимых решений задачи нелинейного программирования имеет вид:  Тогда минимальное значение функции F(х1, х2)= х12 +х22 равно… 0 6 9 16 Вариант 3 1. Пусть - нижняя цена, а - верхняя цена парной игры с нулевой суммой. Тогда верно утверждение… 2 + 2 = 1 + = 0 2. Пусть - нижняя цена, а - верхняя цена парной игры с нулевой суммой. Если = = v, то число v называется … ценой игры точкой равновесия оптимальной стратегией смешанной стратегией 3. Пусть - нижняя цена, а - верхняя цена парной игры с нулевой суммой. Если = , то игра называется… игрой с седловой точкой неразрешимым конфликтом игрой без правил 4. Вектор, каждая из компонент которого показывает относительную частоту использования игроком соответствующей чистой стратегии, называется… смешенной стратегией направляющим вектором вектором нормали градиентом 5. Симплекс-метод - это: аналитический метод решения основной задачи линейного программирования метод отыскания области допустимых решений задачи линейного программирования; графический метод решения основной задачи линейного программирования; метод приведения общей задачи линейного программирования к каноническому виду. 6. Задача линейного программирования состоит в: отыскании наибольшего или наименьшего значения линейной функции при наличии линейных ограничений разработке линейного алгоритма и реализации его на компьютере составлении и решении системы линейных уравнений поиске линейной траектории развития процесса, описываемого заданной системой ограничений. 7. Область допустимых решений задачи линейного программирования не может выглядеть так:     8. Целевой функцией задачи линейного программирования может являться функция: F=12x1+20x2–30x3 →min F= 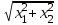 →min →minF= 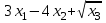 →max →maxF= 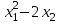 →max. →max.9. Для решения транспортной задачи может применяться… метод потенциалов метод множителей Лагранжа метод Гаусса метод дезориентации 10. В системе ограничений общей задачи линейного программирования … могут присутствовать и уравнения, и неравенства могут присутствовать только уравнения могут присутствовать только неравенства 11. В системе ограничений стандартной (симметричной) задачи линейного программирования … могут присутствовать только неравенства могут присутствовать и уравнения, и неравенства могут присутствовать только уравнения 12. В системе ограничений канонической (основной) задачи линейного программирования … могут присутствовать только уравнения (при условии неотрицательности переменных) могут присутствовать только неравенства (при условии неотрицательности переменных) могут присутствовать и уравнения, и неравенства (при условии неотрицательности переменных) 13. При решении задач целочисленного программирования может применяться … метод Гомори метод множителей Лагранжа метод Гаусса метод аппроксимации Фогеля 14. В основе решения задач методом динамического программирования лежит… принцип оптимальности Беллмана принцип «бритва Оккама» принцип «зуб - за зуб, око- за око» принцип Гейзенберга 15. Нижняя цена матричной игры, заданной платежной матрицей  , … , …меньше верхней цены равна верхней цене не существует 16. Верхняя цена матричной игры, заданной платежной матрицей  , … , …Больше нижней цены равна нижней цене не существует 17. Матричная игра, заданная платежной матрицей  , … , …имеет седловую точку не имеет седловой точки не является парной 18. Цена игры, заданной платежной матрицей  , равна… , равна…22 21 20 23 24 19. Матричная игра, заданная платежной матрицей  , … , …является парной имеет седловую точку не является парной 20. Парная игра с нулевой суммой, заданная своей платежной матрицей, может быть сведена к … задаче линейного программирования задаче нелинейного программирования целочисленной задаче линейного программирования классической задаче оптимизации |
