|
|
Теория игр. К_Р ПО ИГРАМ. Задача по отношению к исходной 1 Целевая функция исходной задачи (1)(3) задается на максимум, а целевая функция двойственной (4)(6) на минимум
К/Р ПО ИГРАМ
7. Сущность понятия прямой и двойственной задачи линейного программирования
Каждой задаче ЛП можно определенным образом сопоставить некоторую другую задачу ЛП, называемую двойственной или сопряженной по отношению к исходной или прямой. 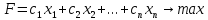 при условиях: при условиях:
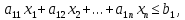
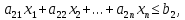
….
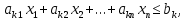 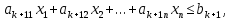
…
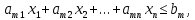

Определение 1. Задача, состоящая в нахождении минимального значения функции называется двойственной по отношению к задаче (1)-(3). Задачи (1)-(3) и (4)-(6) образуют пару задач, называемую в линейном программировании двойственной парой.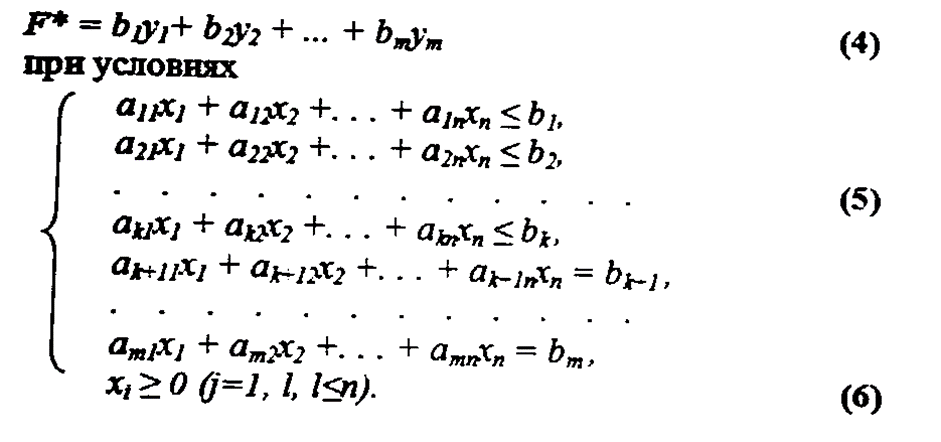
8. Правила, по которым составляется двойственная задача по отношению к исходной
1 Целевая функция исходной задачи (1)-(3) задается на максимум, а целевая функция двойственной (4)-(6) - на минимум.
2. Матрица, составленная из коэффициентов при неизвестных в системе ограничений (2) исходной задачи (1)-(3)
(  ) )
A= | | |
|... … … … |
(
и аналогичная матрица в двойственной задаче (4)-(6) получаются друг из друга транспонированием (т.е. заменой строк столбцами, а столбцов - строками).
( 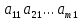 ) )
A^T= |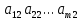 | |
|... … … … |
(
3. Число переменных в двойственной задаче (4)-(6) равно числу соотношений в системе (2) исходной задачи (1)-(3), а число ограничений в системе (5) двойственной задачи - числу переменных в исходной задаче.
Коэффициентами при неизвестных в целевой функции (4) двойственной задачи (4)-(6) являются свободные члены в системе (2) исходной задачи (1)-(3), а правыми частями в соотношениях системы (5) двойственной задачи - коэффициенты при неизвестных в целевой функции (1) исходной задачи.
5. Если переменная xi, исходной задачи (1)-(3) может принимать только лишь положительные значения, то j-е условие в системе (5) двойственной задачи (4)-(6) является неравенством вида >=. если же переменная xi может принимать как положительные, так и отрицательные значения, то j-e соотношение в системе (5) представляет собой уравнение. Аналогичные связи имеют место между ограничениями (2) исходной задачи (1)-(3) и переменными двойственной задачи (4)-(6). Если i-е соотношение в системе (2) исходной задачи является неравенством, то i-я переменная двойственной задачи yi >=0. В противном случае переменная yi может принимать как положительные, так и отрицательные значения.
Двойственные пары задач обычно подразделяют на симметричные и несимметричные. В симметричной паре двойственных задач ограничения (2) прямой задачи и соотношения (5) двойственной задачи являются неравенствами вида >=. Таким образов, переменные обеих задач могут принимать только лишь неотрицательные значения.
9. Связь между решениями прямой и двойственной задач
Каждая из задач двойственной пары является самостоятельной задачей ЛП и может быть решена независимо одна от другой. Однако при определении симплексным методом оптимального плана одной из задач тем самым находится решение и другой задачи.
Лемма 1. Если Х - некоторый план исходной задачи, а Y - произвольный план двойственной задачи, то значение целевой функции исходной задачи при плане Х всегда не превосходит значения целевой функции двойственной задачи при плане Y, т.е. F(X)<=F*(Y)
Лемма 2. Если F(X*)=F*(Y*) для некоторых планов X* и Y* двойственных задач, то X* - оптимальный план исходной задачи, а Y* - оптимальный план двойственной задачи.
Теорема 1 (первая теорема двойственности). Если одна из пары двойственных задач, имеет оптимальный план, то и другая имеет оптимальный план и значения целевых функций задачи при их оптимальных планах равны между собой, т.е. Fmax=F*min
Если же целевая функция одной из пары двойственных задач не ограничена(для исходной - сверху, для двойственной - снизу), то другая задача вообще не имеет планов. Теорема 2 (вторая теорема двойственности). План Х*=(x*1, x*2,...,x*n) прямой задачи и план Y*=(y*1, y*2,...,y*m) двойственной задачи являются оптимальными планами этих задач тогда и только тогда, когда для любого j (j=1,...,n) выполняется равенство 
10. Геометрическая интерпретация двойственных задач
1) обе задачи имеют планы;
2) планы имеет только одна задача;
3) для каждой задачи двойственной пары множество планов пусто.

• Как видно из рис1 максимальное значение ЦФ исходной задачи принимает в т.В. Следовательно, Х*=(2;6), F(X*)=46
• Минимальное значение ЦФ двойственной задачи принимает в точке Е. Y*=(1;4), F(Y*)=46
• Таким образом, значения целевых функций исходной и двойственной задач при их оптимальных планах равны между собой.
• Из рис1 видно, что при всяком плане исходной задачи значение целевой функции не больше 46. Одновременно, как видно из рис2, значение целевой функции двойственной задачи при любом ее плане не меньше 46.
• Таким образом, при любом плане исходной задачи значение целевой функции не превосходит значения целевой функции двойственной задачи при ее произвольном плане
Если основная задача линейного программирования имеет оптимальный план X*, то Y* =  является оптимальным планом двойственной задачи. является оптимальным планом двойственной задачи.
Таким образом, если найти симплексным методом оптимальный план прямой задачи, то, используя последнюю симплекс-таблицу, можно определить 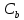 и и 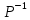 и с помощью соотношения Y* = и с помощью соотношения Y* =  найти оптимальный план двойственной задачи. найти оптимальный план двойственной задачи.
12. Общая постановка транспортной задачи
Общая постановка ТЗ состоит в определении оптимального плана перевозок некоторого однородного груза из пунктов отправления в пункты на
значения. При этом, в качестве критерия оптимальности обычно берется минимальная стоимость перевозок всего груза.
Математическая постановка задачи состоит в определении минимального значения функции: 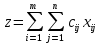 где где 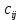 - это тарифы перевозки груза из i-го пункта отправления в j-й пункт назначения - это тарифы перевозки груза из i-го пункта отправления в j-й пункт назначения
При условиях:
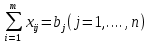

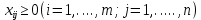
Где 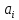 - это запасы груза в i-ом пункте отправления, - это запасы груза в i-ом пункте отправления, 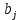 - это потребности в грузе в j-ом пункте назначения - это потребности в грузе в j-ом пункте назначения
Обычно исходные данные ТЗ записывают в виде таблицы
13. Открытая и закрытая модели ТЗ. Как свести открытую модель к закрытой
Закрытой ТЗ называется, если количество груза в пунктах отправления равно потребности в грузе в пунктах назначения: 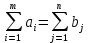
Открытой же будет задача, если это условие не выполняется
Если имеет место открытая транспортная задача, ее необходимо свести к закрытой:
1) в случае перепроизводства – ввести фиктивного потребителя с необходимым объемом потребления (элементы матрицы сij, связывающие фиктивные пункты с реальными, имеют значения, равные затратам на хранение не вывезенных грузов);
2) в случае дефицита – ввести фиктивного поставщика с недостающим объемом отправляемых грузов (элементы матрицы сij, связывающие фиктивные пункты с реальными, имеют значения, равные штрафам за недопоставку продукции).
14. Определение опорного плана ТЗ методом северо-западного угла
Опорный план, как и для всякой задачи линейного программирования, транспортной задачи является и оптимальным планом
При нахождении опорного плана транспортной задачи методом северно-западного угла, заполнение клеток таблицы условий начинают с верхней левой клетки K11 поэтому метод и называется "метод северно западного угла").
https://matworld.ru/linear-programming/transportnaya-zadacha.php#par3
15. Определение опорного плана ТЗ методом минимального элемента
В методе минимального элемента выбор пунктов отправления и пунктов назначения производится ориентируясь на тарифы перевозок, т.е. в каждом шаге нужно выбрать клетку с минимальным тарифом перевозок. Если таких клеток несколько, то выбираем один из них. Надо отметить, что при данном методе определения заполняемой клетки, стоимость перевозок как правило бывает меньше, чем при методе северно западного угла. Поэтому целесообразно начальный опорный план найти методом минимального элемента.
Суть метода аппроксимации Фогеля заключается в следующем. Для каждой строки и для каждого столбца находим разности между двумя записанными в них минимальными тарифами. Полученные разности записываем в специально отведенные для этого столбце и в строке в таблице условий задачи.
Среди указанных разностей выбираем максимальную. В строке (или в столбце), которой данная разность соответствует, определяем минимальный тариф. Клетку, в которой он записан заполняем на данной итерации.
Если минимальный тариф одинаков для нескольких клеток данной строки (столбца), то для заполнения выбираем ту клетку, которая соответствует наибольшей разности между двумя минимальными тарифами в данном столбце (строке).
Применение метода аппроксимации фогеля позволяет получить либо опорный план, близкий к оптимальному, либо сам оптимальный план.
17. Метод потенциалов
1.Нахождение опорного плана; при этом число заполненных клеток должно быть равным n+m-1 (в некоторых клетках могут быть нули). Полученный опорный план следует проверить на оптимальность;
Теорема 2. Если для некоторого порного плана Х ТЗ существуют такие числа что
 для занятых клеток и для занятых клеток и 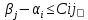 для пустых клеток для пустых клеток
i=1,...,m и j=1,...,n, то Х - оптимальный план ТЗ
Числа 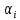 и и  , называются потенциалами ТЗ , называются потенциалами ТЗ
2. Нахождение потенциалов Bj и Ai соответственно пунктов назначения и отправления из системы уравнений  , составленных для занятых клеток. Так как число занятых клеток n+m-1, то число уравнений системы на единицу меньше числа переменных n+m, следовательно, одно из неизвестных можно задать равным произвольному число, традиционно A1=0 и найти методом подстановки остальные; , составленных для занятых клеток. Так как число занятых клеток n+m-1, то число уравнений системы на единицу меньше числа переменных n+m, следовательно, одно из неизвестных можно задать равным произвольному число, традиционно A1=0 и найти методом подстановки остальные;
3. Определение числа Aij=Bj-Ai-Cij для каждой свободной клетки; если среди чисел Aij нет положительных, то получен, оптимальный план транспортной задаче; если же они имеются, то переход к новому опорному плану:
4. Выбор среди положительных чисел Aij максимального, построение свободной клетки, которой оно соответствует, цикл пересчета и сдвиг по циклу пересчета.
Циклом в таблице условий транспортной задачи называется ломаная линия, вершины которой расположены в занятых клетках таблицы, а звенья - вдоль строк и столбцов, причем в каждой вершине цикла встречается ровно два звена, одно из которых находится в строке, а другое - в столбце. Если ломаная линия, образующая цикл, пересекается, то точки самопересечения не являются вершинами.
Правило 1. Каждой из клеток, связанных циклом с данной свободной клеткой, приписывают определенный знак, причем свободной клетке - знак плюс, а всем остальным клеткам - поочередно знаки минус и плюс.
Правило 2. В данную свободную клетку переносят меньшее из чисел xij, стоящих в минусовых клетках. Одновременно это число прибавляют к соответствующим числам, стоящим в плюсовых клетках, и вычитают из чисел. стоящих в минусовых клетках. Клетка, которая ранее была свободной, становится запятой, а минусовая клетка, в которой стояло минимальное из чисел xij, считается свободной.
В результате указанных выше перемещений в пределах клеток, связанных циклом с данной свободной клеткой, определяют новый опорный план транспортной задачи.
Описанный выше переход от одного опорного плана транспортной задачи к другоме ее опорному плану называется сдвигом по циклу пересчета.
При сдвиге по циклу пересчета число занятых клеток остается неизменным, а именно остается равным n+m-1. При этом если в минусовых клетках имеется два (или более) одинаковых числа xij, то освобождают лишь одну из таких клеток, а остальные оставляют занятыми(с нулевыми поставками).
5. Проверка полученного опорного плана на оптимальность, т.е. повтор всех действий, начиная с 2-го этапа. |
|
|
 Скачать 91.81 Kb.
Скачать 91.81 Kb.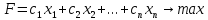 при условиях:
при условиях: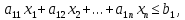
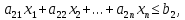
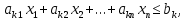
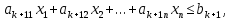
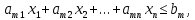

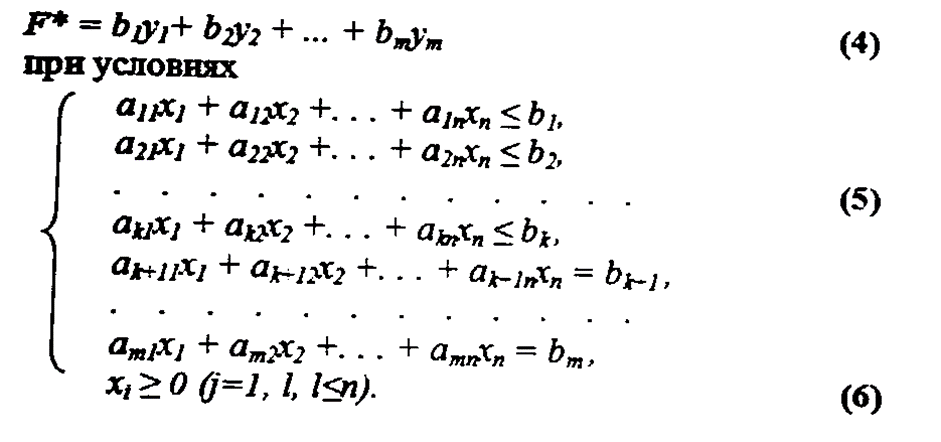
 )
) |
| 
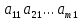 )
)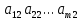 |
| 



 является оптимальным планом двойственной задачи.
является оптимальным планом двойственной задачи.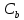 и
и 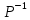 и с помощью соотношения Y* =
и с помощью соотношения Y* = 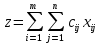 где
где 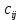 - это тарифы перевозки груза из i-го пункта отправления в j-й пункт назначения
- это тарифы перевозки груза из i-го пункта отправления в j-й пункт назначения 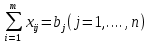

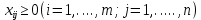
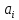 - это запасы груза в i-ом пункте отправления,
- это запасы груза в i-ом пункте отправления, 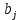 - это потребности в грузе в j-ом пункте назначения
- это потребности в грузе в j-ом пункте назначения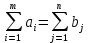
 для занятых клеток и
для занятых клеток и 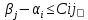 для пустых клеток
для пустых клеток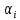 и
и  , называются потенциалами ТЗ
, называются потенциалами ТЗ