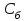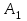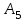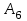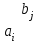Переменными задачи об оптимальном распределении ресурсов
 Скачать 36.94 Kb. Скачать 36.94 Kb.
|
|
3 Переменными задачи об оптимальном распределении ресурсов 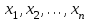 являются: являются:количество продукции видов  , которое планирует выпускать предприятие; , которое планирует выпускать предприятие;запасы сырья (ресурса), которым обладает предприятие; количество денежных средств, затраченных на производство продукции; количество сырья, идущее на производство единицы продукции каждого вида. Задача линейного программирования решается графическим способом, если в задаче одна переменная; две переменные; четыре переменные; любое число переменных. Целевая функция ЗЛП достигает своего минимального или максимального значения во внутренней точке области допустимых решений; в угловой точке области допустимых решений; в граничной точке области допустимых решений; в любой точке области допустимых решений. Оптимальность плана в симплексной таблице определяется 1) по столбцу свободных членов b; 2) по индексной строке 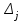 ; ;3) по разрешающей строке; 4) по разрешающему столбцу. Если матрица коэффициентов при неизвестных исходной задачи линейного программирования имеет вид 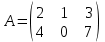 , то матрица коэффициентов двойственной задачи будет иметь вид: , то матрица коэффициентов двойственной задачи будет иметь вид: Коэффициентами при неизвестных целевой функции двойственной задачи являются 1) коэффициенты при неизвестных целевой функции исходной задачи; 2) свободные члены системы ограничений исходной задачи; 3) неизвестные исходной задачи; 4) коэффициенты при неизвестных системы ограничений исходной задачи. Потенциалами транспортной задачи размерности (mxn) называются m+n чисел ui и vj, для которых выполняются условия 1) ui+vj=cij для занятых клеток; 2) ui+vj=cij для свободных клеток; 3) ui+vj=cij для первых двух столбцов распределительной таблицы; 4) ui+vj=cij для первых двух строк распределительной таблицы. Первоочередной задачей предприятия является снижение производственных издержек, которые можно уменьшить за счет изменения объемов 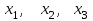 выпуска изделий. Издержки производства известны, и составляют 120, 371 и 255 усл.ден.ед. на единицу каждого выпускаемого изделия соответственно. Как в этом случае можно записать целевую функцию задачи оптимизации? выпуска изделий. Издержки производства известны, и составляют 120, 371 и 255 усл.ден.ед. на единицу каждого выпускаемого изделия соответственно. Как в этом случае можно записать целевую функцию задачи оптимизации? Дана задача линейного программирования. 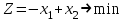 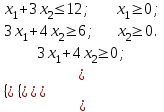 Привести задачу к каноническому виду, заполнить симплексную таблицу. Имеет ли задача начальный базис?
Построить систему потенциалов для транспортной задачи, заданной таблицей
 - запасы поставщиков; - запасы поставщиков;  - запросы потребителей. - запросы потребителей. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||