В транспортной задаче оптимальный план будет не единственный если
 Скачать 2.94 Mb. Скачать 2.94 Mb.
|
|
В транспортной задаче оптимальный план будет не единственный если: а) n+m-1 число свободных клеток в таблице б) оценки свободных клеток Sij не равно 0 (НЕТ) в) оценки свободных клеток Sij ≤0 г) хотя бы одна клетка свободной клетки Sij=0 (ДА) В задаче определения наиболее экономического маршрута шагом является: а) километр б) день (НЕТ) в) перемещение из одной группы населенных пунктов в другую (ДА) В прямоугольной системе координат множество точек, удовлетворяющих ограничению
В задачах линейной оптимизации: Целевая функция и состояние системы- линейные алгебраические модели В Exсel для решения задач нелинейного программирования реализованы методы: Ньютона и метод сопряженных градиентов Все вычисления, дающие возможность найти оптимальное значение эффекта…… а) производятся на основании основного функционального…… ДА б) производятся на основании обыкновенных жордановых…. в) производятся на основании метода прямого воздействия В чем заключается ограниченность применения графического метода решения задач нелинейного программирования? позволяет решать задачи с ограниченным числом неизвестных (как правило с двумя неизвестными величинами) В задаче о распределении ограниченных ресурсов: Если ресурс израсходован полностью, то соответствующая двойственная переменная больше нуля Если ресурс не израсходован, то соответствующая двойственная переменная равна нулю В какой из транспортных таблиц содержится опорный план: А) 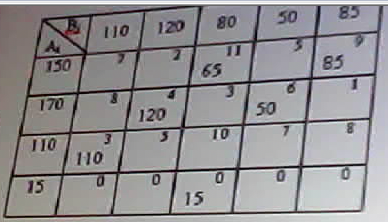 Б) Б) 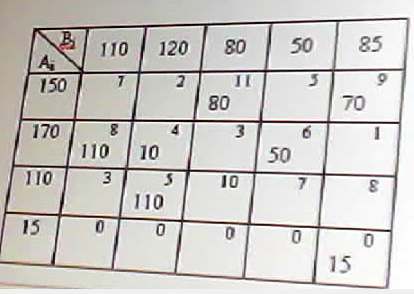 В) 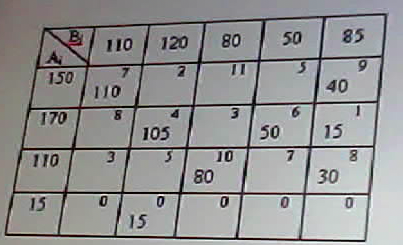 г) г) 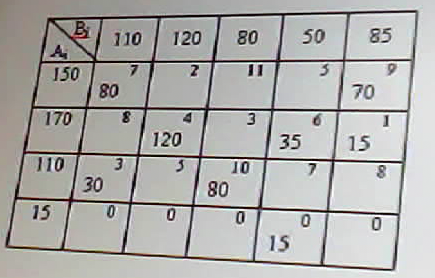 А Б В НЕТ Г Верно ли, что оптимальным планом или оптимальным решением задачи линейного программирования называется план, доставляющий наименьшее (наибольшее) значение линейной функции. а) нет; б) да. В математическом программировании рассматриваются задачи: а) линейной оптимизации; б) нелинейной оптимизации; в) целочисленной оптимизации; г) динамического программирования; д) стохастической оптимизации; е) все задачи, перечисленные в пунктах а), б), в), г) и д). Выберете из следующих утверждений правильное: а) область допустимых решений задачи линейной оптимизаций всегда ограничена; б) область допустимых решений задачи линейной оптимизации всегда выпукла; в) область допустимых решений задачи линейной оптимизации может состоять из нескольких разрозненных областей. В задачах нелинейной оптимизации: возможны любые из вариантов перечисленных выше В задачах нелинейной оптимизации экстремальное значение целевой функции: возможны любые из перечисленных вариантов В рассмотренной модели транспортной задачи предполагается перевозка: а) однородного продукта; б) разнородных продуктов; в) разнородных комплектов; г) всевозможных материалов. В ограничениях линейных задач оптимального использования ограниченных ресурсов дополнительные (балансовые) переменные означают: а) величины неиспользованных ресурсов; б) убыток, получаемый от использования ресурсов; в) оценку дефицитности ресурсов; г) количество ресурсов. В ограничениях линейных задач оптимального составления рациона дополнительные (балансовые) переменные показывают: а) недостаточное потребление соответствующего компонента; б) оценку дефицитности компонента; в) цену компонента; г) количество компонента; д) потребление соответствующего компонента сверх нормы. Величина двойственной оценки задачи линейной оптимизации численно равна: а) величине изменения значения целевой функции при изменении соответствующего ресурса на единицу; б) значению свободной переменной; в) оптимальному объему выпускаемой продукций. В задаче параметрического линейного программирования: могут выполняться оба условия в) и г) Все вычисления, дающие возможность найти оптимальное значение эффекта, достигаемого за п шагов в задаче динамического программирования: а) производятся на основании основного функционального уравнения или рекуррентного соотношения; б) производятся на основании обыкновенных жордановых исключений; в) производятся на основании метода прямого воздействия. Во всех ли задачах динамического программирования процесс решения естественно является многошаговым (многоэтапным)? а) да, во всех; б) не во всех. Для некоторых задач разбиение на шаги (этапы) осуществляется искусственно, как, например, в задаче загрузки самолета предметами различных типов; в) в большинстве задач. Вычислительная процедура решения задачи динамического программирования включает два этапа: а) построение области допустимых решений б) нахождение начального опорного плана и дальнейшего его улучшения вплоть до получения оптимального в) условная и безусловная оптимизация (ДА) г) подготовка данных и построение модели В задаче целочисленного линейного программирования, решаемой методом ветвей и границ, на максимум получены на обеих ветвях равные значения целевой функции какую из задач необходимо ветвись дальше: Исходную по другой переменной В задаче целочисленного линейного программирования, решаемой методом ветвей и границ, на минимум получены на первой ветви значение целевой функции 200,5 , а во второй 198,2 какую из задач необходимо ветвись дальше: Первую В чем состоит суть метода Гомори? а) в преобразовании симплексных таблиц; б) в экстраполяции неизвестных; в) в нахождении целочисленного решения последовательными отсечениями от области допустимых решений нецелочисленных точек, пока целочисленная точка не станет угловой (крайней). В линейной задаче оптимизации распределения ресурсов дополнительные переменные означают: величины неиспользованных ресурсов Выберете верное утверждение: а) область допустимых решений задачи линейной оптимизации может состоять из нескольких разрозненных областей; б) область допустимых решений задачи линейной оптимизации всегда ограничена; в) область допустимых решений задачи линейной оптимизации всегда выпукла. Вычислить длину вектора градиента функции в точке (1,1,1) к целевой функции 13 В опорном плане транспортной задачи должно быть следующее количество заполненных клеток: а) m-n+1; б) m-n-1; в) m+n-1; (ДА) г) m+n+1. Вычислить значения главных миноров матрицы Гессе функции z=2x12+x22-x1x2+5x1-6x2+10 7; 4; Вычислить сумму множителей Лагранжа для решения задачи на условный экстремум функции Z=х12+х22+х1х3 х1+х2-4=0 х2+х3-6=0 хi>=0 -6 Вычислить значение целевой функции Z=х12+х1х2 в точке условного экстремума х1+2х2-4=0 хi>=0 в точке (0,2) 0 Вычислить суммарную максимальную прибыль получаемую предприятием от реализации продукции х1 и х2 в моменты времени t= 0; 0,5; 1. Расход ресурсов определен неравенствами 4x1+ 3x2<=12 4x1+ x2 <=8 , рентабельность продукции х1 изменяется по закону f1(t)=12t , а продукции x2 f2(t)=8(1-t) , параметр t изменяется в пределах [0,1] Нету ответа Геометрической интерпретацией целевой функции в задаче линейного программирования с двумя переменными является: а) точки на плоскости; б) многоугольник планов; в) линии уровня. Граф содержащий маршрут, в который входят все ребра называется: Гамильтоновым Граф содержащий маршрут, в который входят все вершины называется: Эйлеровым Граф называется взвешенным если: С каждым ребром графа связано число Граф называется ориентированным, если для него: Если для задания ребра важен порядок определяющих вершин Для нахождения оптимальных смешанных стратегий игры решаются задачи: решаются двойственные задачи линейного программирования Для решения транспортной задачи на ЭВМ можно использовать: а) пакет прикладных программ QSB б) команду Поиск решения из меню Сервис информационных технологий Exel Для проведения сбалансированности транспортной задачи необходимо: ввести фиктивных поставщиков в или потребителей Для прямой задачи max z =2х1+3х3 x1+x2<=10 x2+3x3<=20 двойственная задача имеет вид: 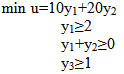 Для прямой задачи max z=-2х1+х2+3x3 -2x1+3x2+x3+x4=10 x1+ x2-2x3+x5=20 хi>=0 двойственная задача имеет вид min u=10y1+20y2 -2y1+3y2>= -2 3y1+y2>=1 y1-2y2>=3 Для прямой задачи min z=2х1+3х2+x3 x1+x2+x3<=20 5<=x3<=10 двойственная задача имеет вид: 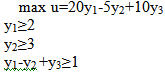 Для прямой задачи min z =2х1+x3 x1+x2<=10 1<=x2<=5 x3<=10 двойственная задача имеет вид: 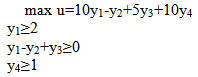 Двойственная оценка численно равна: г) Допустимое решение транспортной задачи является опорным, если: а) оно получено симплексным методом; б) в этом решении заполненные клетки таблицы транспортной задачи не образуют ни одного цикла (число заполненных клеток таблицы равно (m=n-l), где m — число поставщиков, a n — число потребителей); в) занятые в этом решении клетки образуют циклы, Допустимое решение транспортной задачи является опорным, если: а) …… клетки таблицы транспортной задачи не образуют ни одного цикла и число заполненных клеток таблицы равно (……) где m – число поставщиков, n – число потребителей. ДА б) в этом решении заполненные клетки таблицы транспортно задачи не образуют ни одного цикла и число заполненных клеток меньше (…….) где m – число поставщиков, n – число потребителей. НЕТ в) …… в этом решении клетки образуют клетки. Из инета - Допустимое решение транспортной задачи X=(xij) является опорным тогда и только тогда, когда из занятых клеток таблицы нельзя образовать ни одного цикла. Дана транспортная задача: Какое число будет вписано первым в клетку по методу минимального тарифа (эле….)
а) 12 или это б) 5 в) 20 г) 8 или это д) 9 Дана транспортная задача …………. Какое число будет вписано первым в клетку…….
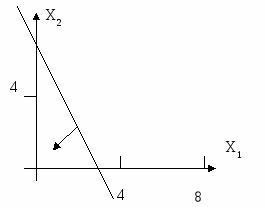
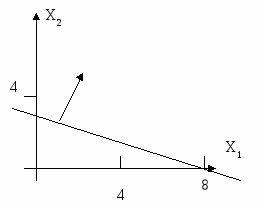
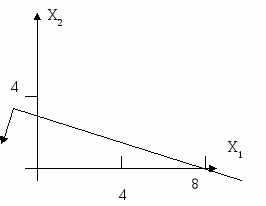
а) 10 б) 5 в) 2 г) 8 (НЕТ) д) 9 Дана математическая модель. Определить сколько …… будет иметь:  7 3 (НЕТ) 4 ?? Д 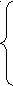 ана математическая модель и область допустимых решений. Необходимо определить координаты вектора-градиента функции: ана математическая модель и область допустимых решений. Необходимо определить координаты вектора-градиента функции:f=3x1+4x2 (max) 2x1-x2 ≤8 5х1+3х2≤15 х1≥0 х2≥0 а) (3;4) (ДА) б) (5;3) в) (2;-1) г) (8;15) Допустимое решение транспортной задачи является опорным, если а) в этом решении заполненные клетки таблицы транспортной задачи не образуют ни одного цикла (число заполненных клеток таблицы равно (m+n-1), где m- число поставщиков, а n- число потребителей); б) оно получено симплексным методом; в) в этом решении заполненные клетки таблицы транспортной задачи образуют циклы (число заполненных клеток таблицы равно (m+n+1), где m- число поставщиков, а n- число потребителей). Для решения задач динамического программирования используется: функционально- рекуррентное соотношение Р Беллмана Для решения задачи сетевого планирования: Матрица инцидентностей графа Для следующей транспортной таблицы если значение потенциала U1= -5, то значение потенциала U? будет равно:
а) -2 НЕТ б) -3 ДА в) 5 г) 10 Для следующей транспортной таблицы если значение потенциала V1 = 7, то …… 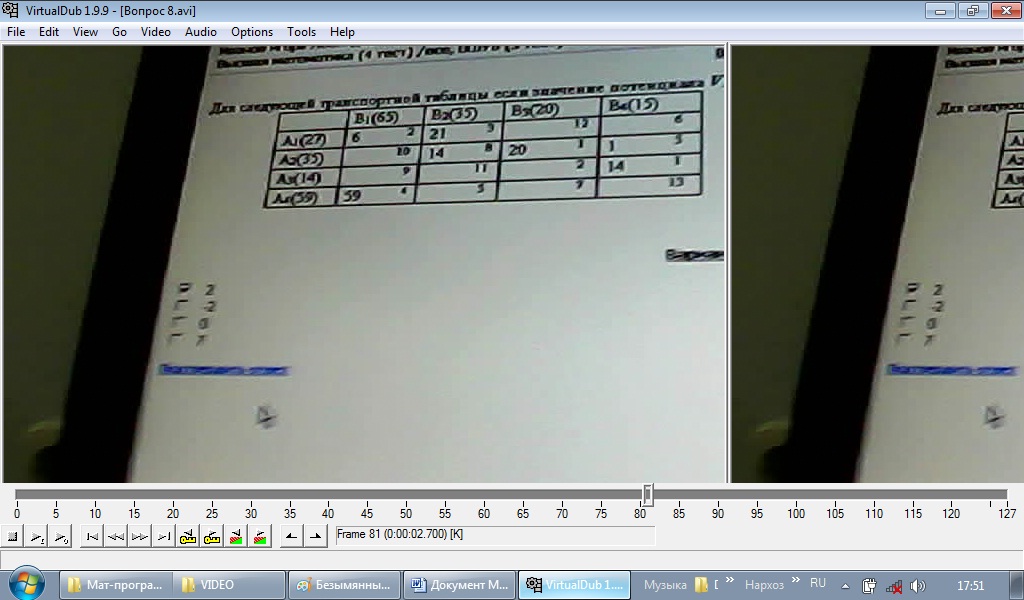 а) 2 НЕТ б) – 2 в) 0 г) 7 Для следующей транспортной таблицы оценка свободной клетки (1; 3) равна: 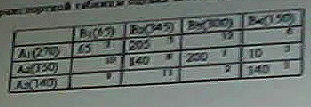 16 2 12 -9 6 (НЕТ) Для данного опорного плана транспортной задачи по критерию стоимости значение целевой функции будет равно:
а) 136 (или 196) б) 24 НЕТ в) 432 (ДА) г) 462 (тогда этот ответ, если я где-то ошибся в цифрах таблицы |

 )
) )
) ) (ДА)
) (ДА)




 )
)