В транспортной задаче оптимальный план будет не единственный если
 Скачать 2.94 Mb. Скачать 2.94 Mb.
|
|
Если найдено опорное решение транспортной задачи: а) то для каждой свободной клетки этого решения можно образовать единственный цикл; б) то для каждой свободной клетки можно образовать множество циклов; в) то для каждой занятой клетки можно образовать единственный цикл. Если в строке оптимального решения задачи линейной оптимизации есть хотя бы один нулевой элемент, то: а) задача имеет множество оптимальных решений; б) задача не имеет решений; в) задача имеет единственное решение; г) решение задачи не завершено. Если целевая функция одной из взаимо двойственных задач не ограничена, то а) в другой задаче целевая функция тоже не ограничена; б) другая задача не имеет решения; в) другая задача имеет единственное решение. Если Х* оптимальный план исходной (прямой) задачи с целевой функцией f(x)= 6х1+4х2, а y – оптимальный план двойственной к ней с целевой функцией F(y) = 20у1+40у2+25у3, то пара оптимальных планов: а) Х*= (25;20) Y*= (3;6;4) б) Х*= (20;25) Y*= (2;2;4) ДА в) Х*= (22;10) Y*= (4;5;6) г) Х*= (21;23) Y*= (3;5;6) Если х1, х2,х3 , х4 булевы переменные то условие выбора любых двух вариантов из четырех возможных , запишется в виде: х1+ х2+х3 +х4 =2 Если х1, х2,х3 , х4 булевы переменные то условие выбора по крайней мере одного вариантов , запишется в виде х1+ х2+х3 +х4 =1 Если в исходной задаче неизвестная Х1= 9/2, то решая ее методом ветвей и границ, новые подзадачи образуются ограничениями: а) первая подзадача будет содержать условия исходной задачи и дополнительное ограничение Х1 ≤ 4, а вторая подзадача образуется ограничением Х1 ≥ 5 Если задача ЦЛО решается методом ветвей и границ на максимум функции и в первой подзадаче f1max = 2500,25; а во второй f2max = 1900,75. Какую из подзадач при продолжении решения необходимо ветвить дальше? первую Задача ЦЛО решается методом ветвей и границ на максимум функции и в первой подзадаче f1max = 361,36; а во второй f2max = 450,93. Какую из подзадач при продолжении решения необходимо ветвить дальше? первую Задачи исследования операций в экономике это: оптимизации цели системы при ограничениях на множество допустимых состояний системы Задача линейной оптимизации называется вырожденной, если: а) в столбце свободных членов симплексной таблицы имеется по крайней мере один нулевой элемент; б) в столбце свободных членов симплексной таблицы все элементы положительные; в) если в симплексной таблице имеются нулевые элементы. 3а разрешающий столбец при нахождении максимума целевой функции задачи линейной оптимизации выбирается тот: а) в котором находится наименьший отрицательный элемент строки функции, за исключением элемента, находящегося в столбце свободных членов (ДА) б) в котором находится отрицательный элемент строки функции; в) в котором все элементы неотрицательные. НЕТ Задача целочисленного линейного программирования переменные: Принимают целые значения , ограниченные сверху Задачи решаемые методом математического программирования являются: а) любой класс задач б) класс экстремальных задач в) класс задач на экстремум (максимум или минимум) функции со многими неизвестными ДА Задачей нелинейного программирования является задача, у которой: а) нелинейной является целевая функция б) некоторые или все ограничения являются нелинейными в) функция и ограничения являются нелинейными г) выполняется хотя бы одно из условий а, б или в Задача линейного программирования на максимум решается графическим методом. Укажите точку, в которой целевая функция достигает своего максимального значения. 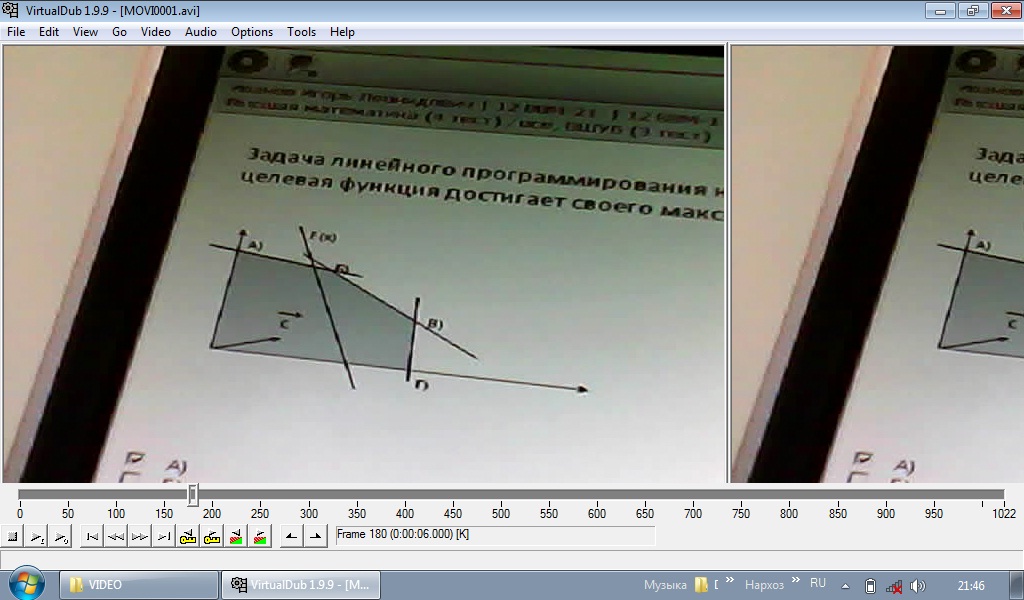 а) А (НЕТ) б) Б ??? в) В г) Г Задача нелинейного программирования с ограничениями неравенствами может быть решена методом множителей Лагранжа если: ограничения неравенства привести к равенствам и наложить условие неотрицательности на дополнительные переменные. Задачу линейного программирования можно решить а) Методом Лагранжа; б) графическим методом; в) методом наименьших квадратов; г) симплексным методом. Задачу максимизации целевой функции Max Z=10Х1+2Х2-3Х3 можно заменить задачей минимизации целевой функции: Z= -10Х1-2Х2+3Х3 Значение целевой функции в задаче Max Z=2x1+x2 при ограничениях х1-х2<=2 х1+3х2>=3 7х1-х2>=2 x1>=0, x2>=0 равно: ∞ Значения неизвестных системы линейных уравнений находятся: а) по формуле Х= А-1 В, где А-1 – обратная матрица к матрице А из коэффициентов при неизвестных системы уравнений; В – вектор-столбец свободных членов Запишите путь ………… длины между пунктами 1 и 9: 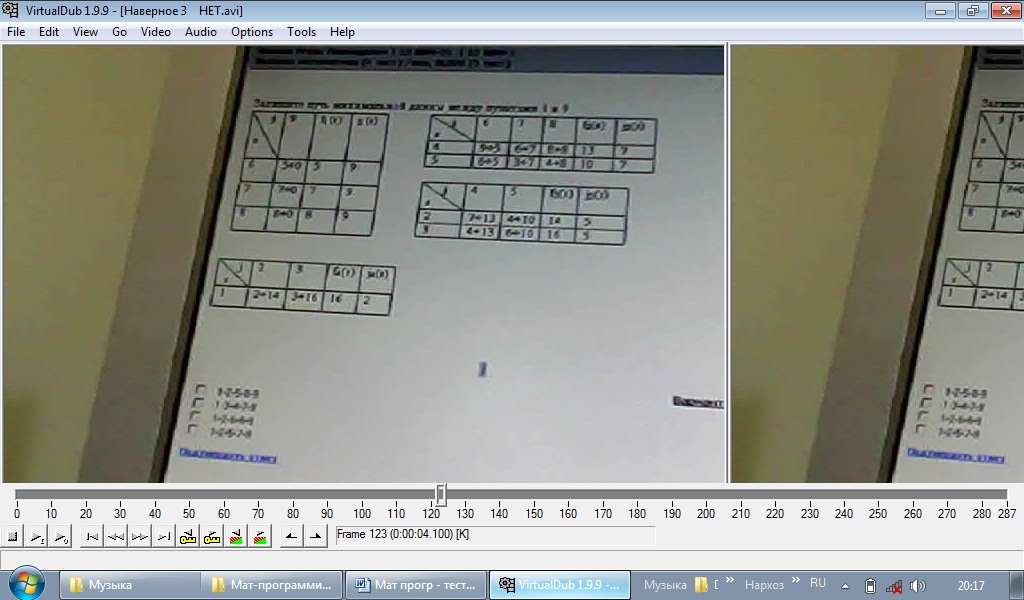 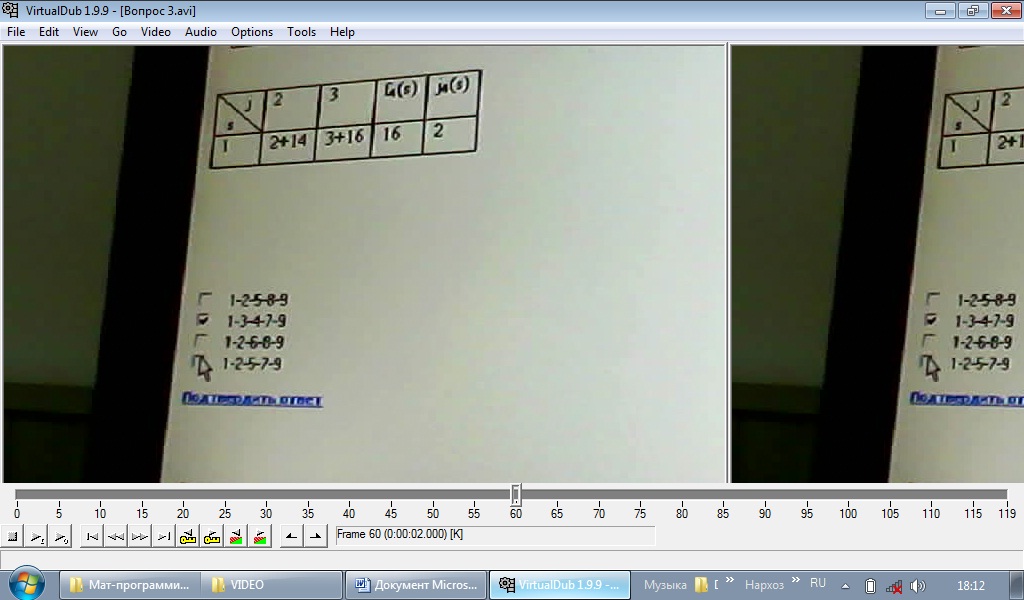 а) 1-2-5-8-9 б) 1-3-4-7-9 НЕТ в) 1-2-6-8-9 НЕТ г) 1-2-5-7-9 Какое программное средство можно использовать для нахождения ранга матриц, обратных матриц, решение систем линейных уравнений и оптимизационных задач? Microsoft Exel Какая функция Exel применяется для нахождения обратной матрицы? Функция МОБР из диалогового окна Мастер функции Какая функция Exel применяется для нахождения произведения матриц? Математическая функция МУМНОЖ из диалогового окна Мастер функции Какая команда Excel применяется для нахождения оптимального решения нелинейных задач? Поиск решения из меню Сервис Когда при решении задачи ЦЛО методом ветвей и границ на максимум функции заканчивается вычислительный процесс? а) когда получено целочисленное решение Каким (или какой) будет оптимальный план для задачи максимизации прибыли согласно даннной симплексной таблицы: 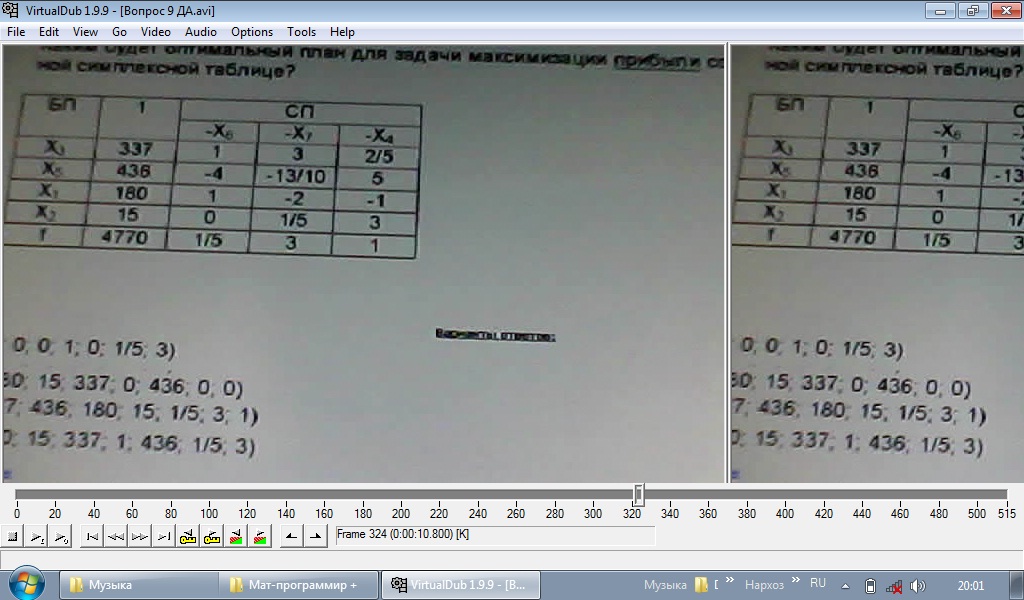 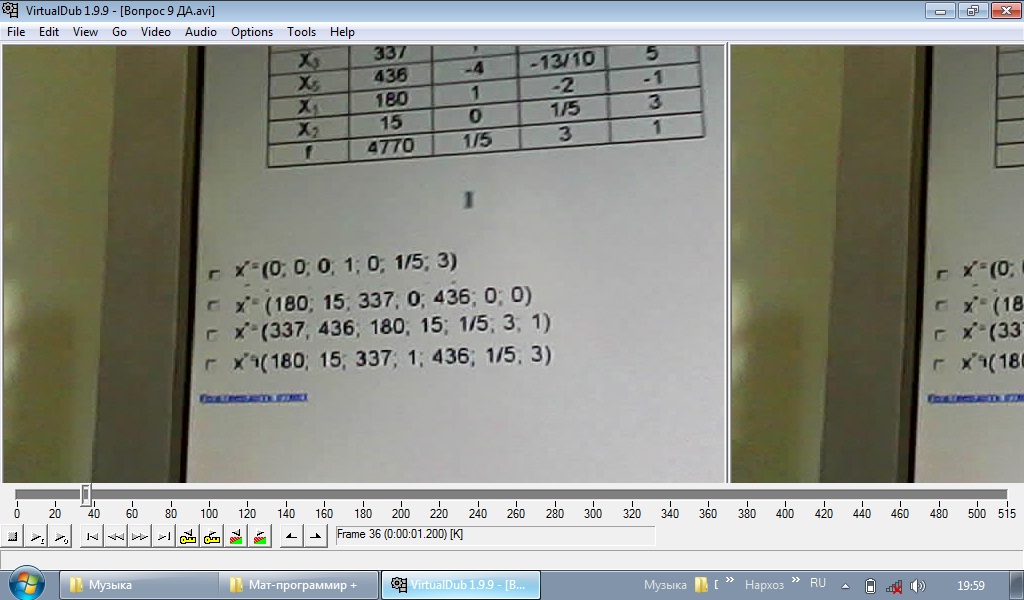 Ответ Б (ДА) Каждой занятой клетке в таблице в транспортной задачи соответствует уравнение: а) ui + vj < cp б) ui + vj =cp ДА в) ui + vj ≥ cp г) ui ∙ vj = cp, где ui и vj - потенциалы Какая команда Microsoft Excel используется для нахождения экстремума функции линейных задач математического программирования? а) Поиск решения из меню Сервис; б) Параметры из меню Сервис; в) Любая команда из меню Сервис. Какое из реккурентных соотношений для решения задачи фрмирования производственной программы по критерию минимизации затрат с учетом ограниченности производственных мощностей и складских площадей для хранения продукции является верным? 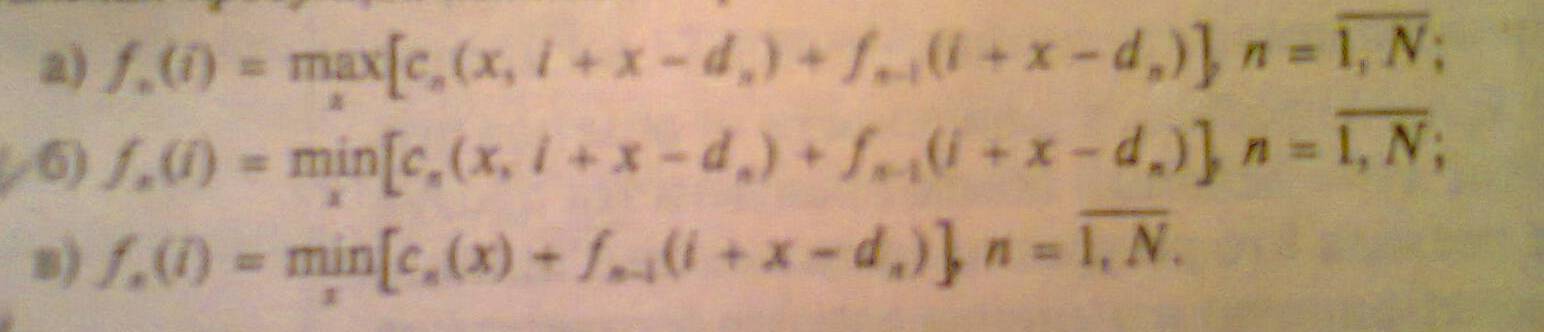 ответ Б Какие из перечисленных элементов включает математическая модель задачи: а) целевую функцию б) теорему в) систему ограничений г) целевую функцию, систему ограничений, совокупность неизвестных (план задачи) х = (х1;……хn) ДА д) доказательство е) график Какие методы относятся к методам нахождения начального опорного плана в транспортной задаче: а) метод аппроксимации; б) метод минимального элемента; в) метод Лагранжа; г) метод Фогеля; д) метод «северо-западного угла». Критерием оптимальности при нахождении минимума функции транспортной задачи служит: а) неотрицательность значений потенциалов; б) неположительность оценок незаполненных клеток транспортной таблицы; в) неотрицательность оценок заполненных клеток транспортной таблицы; г) неотрицательность оценок незаполненных клеток транспортной таблицы. Какое из утверждений верно: а) каждой задаче линейной оптимизации можно поставить в соответствие задачу, называемую двойственной к исходной; (ДА) б) для некоторых типов задач линейной оптимизации существует задача, называемая двойственной к исходной задаче; в) каждой задаче линейной оптимизации можно поставить в соответствие несколько задач, двойственных к исходной. Какое из утверждений верно: а) если исходная задача является задачей максимизации целевой функции, то двойственная - задачей минимизации целевой функции; б) если исходная задача является задачей максимизации целевой функции, то двойственная - также задача максимизации; в) если исходная задача является задачей максимизации, то двойственная может быть как задачей минимизации, так и задачей максимизации. Какое из утверждений верно? а) потенциал i-го поставщика ui (i=1,m) является двойственной оценкой единицы запаса груза этого поставщика. б) потенциал j-го потребителя vj (j=1,n) является двойственной оценкой единицы запаса груза этого поставщика. Какое из утверждений верно? а) двойственные оценки являются показателем дефицитности ресурсов и продукции; б) двойственные оценки являются показателем влияния ограничений на значение функции; в) двойственные оценки являются показателем эффективности производства отдельных видов продукции с позиций критерия оптимальности; г) двойственные оценки являются инструментом сопоставления суммарных затрат и результатов; д) верными являются все утверждения пунктов а), б), в) и г). Какое из утверждений верно? а) задача математического программирования — это задача на экстремум одного неизвестного; б) задача математического программирования — это задача на экстремум функции многих переменных с ограничениями на область их изменения; ДА в) задача математического программирования — это многовариантная задача, позволяющая найти какое-либо решение. Какое из утверждений верно: а) двойственные оценки являются инструментом сопоставления суммарных затрат и результатов. б) верными являются все отверждения в) двойственные оценки являются показателем дефицитности ресурсов и продукции. в) двойственные оценки являются показателем влияния ограничений на значение функции. г) двойственные оценки являются показателем эффективности производства отдельных видов продукции с позиции критерия оптимальности. ДА Какое из утверждений верно? а) динамическое программирование — математический метод для нахождения оптимальных решений многошаговых (многоэтапных) задач; б) динамическое программирование — математический метод для нахождения всевозможных решений задач экономики, физики, биологии; в) динамическое программирование — метод нахождения множества решений задачи управления во временном аспекте; д) динамическое программирование — математический метод для нахождения решений дифференциальных уравнений. Какое из рекуррентных соотношений для решения п-этапной задачи нахождения оптимального маршрута перевозки груза из города А в город В является верным, если S — состояние системы, a j — номер города? 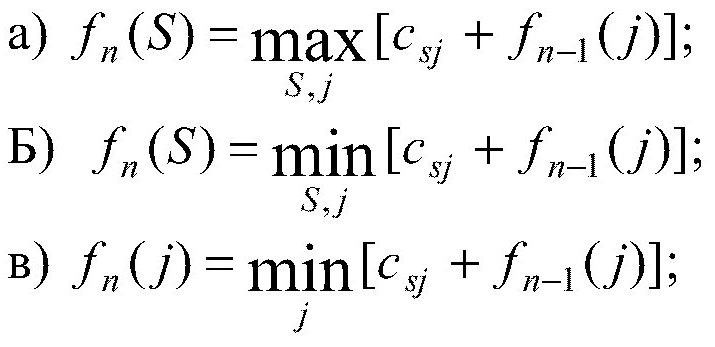 Ответ Б Какое из записанных дополнительных ограничений построено верно по ограничении: 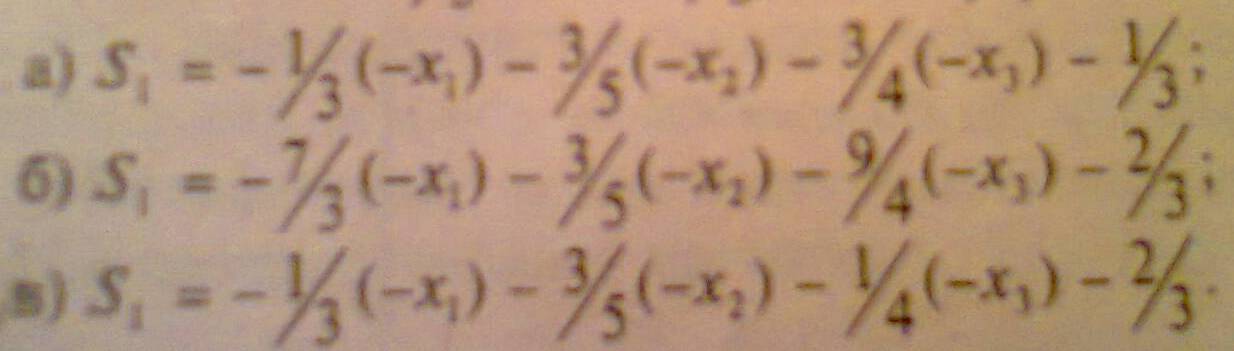 Ответ В Какой командой вызывается диалоговое окно Параметры поиска решения? а) Поиск решения; б) Параметры диалогового окна Поиск решения; в) Выполнить. 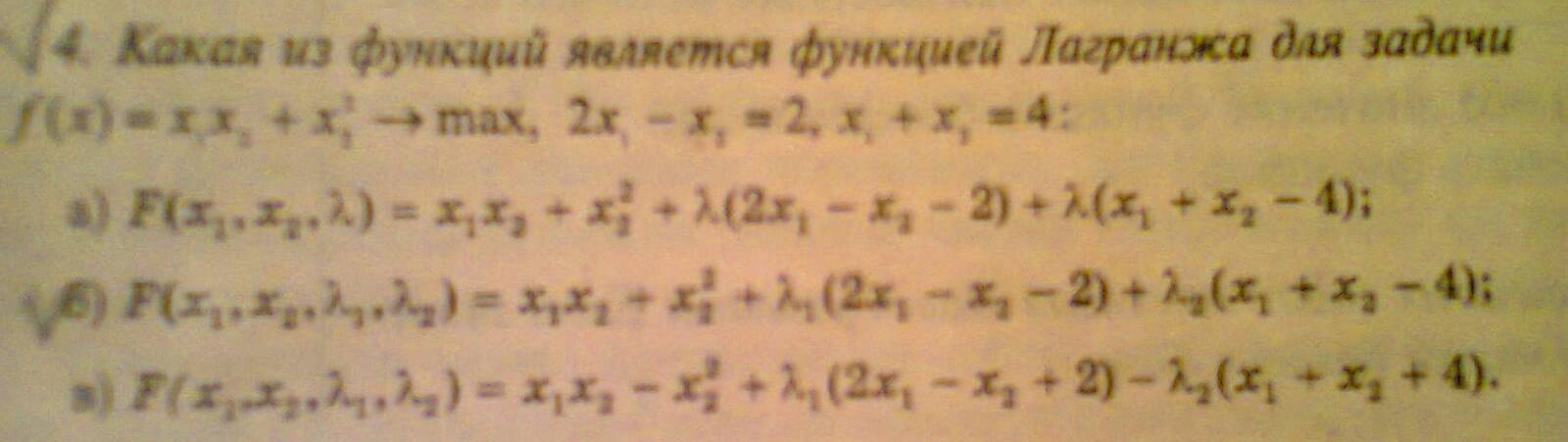 Ответ Б Какие флажки необходимо установить в диалоговом окне Параметры поиска решения для решения линейной оптимизационной задачи? а) Линейная модель; б) Неотрицательные значения; в) Флажки, указанные в пунктах а) и б). Критерием оптимальности при нахождении минимума функции транспортной задачи служит: а) неотрицательность характеристик Sij свободных клеток таблицы транспортной задачи; б) неотрицательность оценок загруженных клеток таблицы транспортной задачи; в) отрицательность оценок загруженных клеток; г) равенство нулю потенциалов. Критическим путем на сетевом графике проекта называется: путь максимальной продолжительности Какие дополнительные условия можно вводить при решении транспортной задачи? а) запрет перевозки от i -го оставщика j-му потребителю; б) фиксированную поставку груза; в) нижнюю границу на поставку груза; г) верхнюю границу на поставку груза; д) все условия, перечисленные в пунктах а) — г) ДА Коэффициенты целевой функции в двумерной задаче линейной оптимизации: указывают направление движение к точке экстремума целевой функции Математическая модель состояний экономической системы описывается: ни каких ограничений на тип уравнений или неравенств не предусмотрено Математическая модель транспортной задачи это: задача линейного программирования Математическая модель целевой функции экономической системы задается: ни каких ограничений на вид целевой функции не предусмотрено Математическая модель задачи линейной оптимизации может быть записана в следующей форме: а) общей; б) симметричной; в) канонической; г) Лагранжа; д) числовой. Математическая модель задачи линейной оптимизации записана в форме: F = 8x1 +6x2 –3x3 (max) 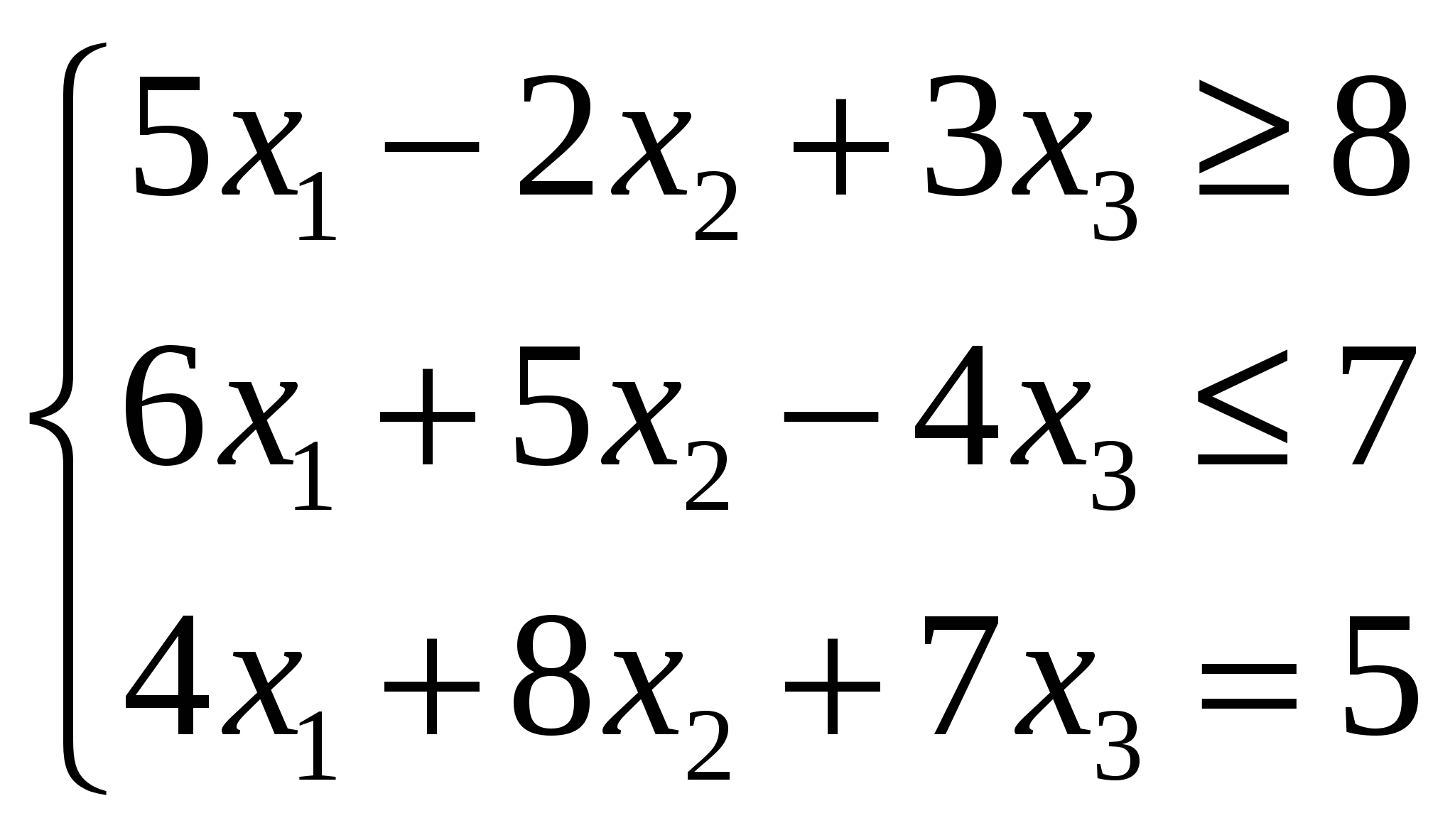 x1≥0, x2≥0, х3≥0. 1) симметричной;
Матрица строки и столбцы которой соответствуют вершинам графа, а элементы число ребер связывающих вершины называется матрицей: Смежности Модель двойственной задачи построенной к данной принимает следующий вид: f = 8х1 - 4х2+ 7х3 2 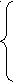 х1+ 3х2 - 4х3 х1+ 3х2 - 4х3 5х1+ 4 х2 + х3 4х1+ 2х2+ 8х3 хj принимает следующий вид:
Матрица строки и столбцы которой соответствуют вершинам и ребрам графа, а элементы 1 или 0 в зависимости от наличия связи между вершинами и ребрами: Инцидентностей Метод Парето: сокращает область поиска компромиссных решений многокритериальной оптимизации Метод при котором для нахождения начального опорного плана записывается число в первую клетку: а) метод Фогеля б) метод северо-западного угла (ДА) в) метод потенциалов г) метод наименьшего элемента Между переменными прямой и двойственной задачи можно: а) установить взаимно однозначное соответствие; б) произвести замену переменных; в) установить регрессионную зависимость между переменными; г) привести подобные члены. Множители Лагранжа λi (i=1,m) показывают: на сколько изменится значение функции в оптимальном решении при изменении правой части i-го ограничения на единицу: Модель транспортной задачи это: а) модель задачи линейной оптимизации; б) модель сетевого планирования в) модель динамического программирования или это. Модифицированные жордановы исключения применяются для нахождения: а) обратной матрицы; б) ранга матрицы; в) решений систем линейных уравнений; г) решения задач оптимизации; д) всего перечисленного в пунктах а), б), в) и г). Начальный опорный план транспортной задачи ищется методом: Северо-западного угла Фогеля Начальный опорный план транспортной задачи можно составить: а) методом Жордана; б) методом минимальной стоимости; в) методом аппроксимации; г) методом Фогеля; д) применяя методы пунктов б) и г). Найдите верные утверждения применительно к задаче рационального использования ограниченных ресурсов: а) двойственные оценки в оптимальном решении задачи характеризуют дефицитность ресурсов; б) ресурс, полностью использованный в оптимальном решении, является дефицитным, его двойственная оценка — больше нуля; в) если ресурс расходован не полностью, то он избыточен, его двойственная оценка равна нулю; г) если ресурс расходуется не полностью, то он избыточен, его двойственная оценка больше нуля. На рисунке изображен случай, когда своего максимального значения функция f(х) достигает
Найдите правильное преобразование неравенства 11Х1 + 3Х2 > -19 -11Х1 – 3Х2 < 19 Область допустимых решений задачи линейной оптимизации: а) может быть объединением двух выпуклых многоугольников НЕТ б) может быть окружностью в) может образовывать невыпуклый многоугольник с отрицательными координатами вершин. г) может быть пустым множеством (ДА) Область допустимых решений задачи линейной оптимизации: а) может быть пустым множеством; б) не может быть пустым множеством; в) может быть точкой; г) может быть отрезком прямой; д) может быть окружностью; е) может образовывать выпуклый многоугольник (в пространстве — многогранник). Область допустимых решений задачи нелинейного программирования может быть: а) выпуклой б) вогнутой в) из нескольких частей г) выпуклой, вогнутой и состоять из нескольких частей Основным принципом, на котором базируется оптимизация в задачах динамического программирования, является: а) принцип оптимальности Р. Беллмана; б) принцип особенностей вычислительного метода; в) принцип планового соответствия переменных; г) принцип дуализма. Оценка свободной клетки ( 2; 1) равна
Особенность решения задачи динамического программирования заключается в том, что: а) дальнейшее поведение состояния системы зависит только от данного состояния и не зависит от того, каким путем система пришла в это состояние; б) управление на каждом шаге выбирается с учетом всех погрешностей; в) управление на каждом шаге выбирается с учетом валентности состояний. Оптимальный план задачи линейного программирования: а) допустимый план, удовлетворяющей системе ограничений задачи б) план удовлетворяющий всем условиям задачи, и доставляющий экстремум целевой функции. ДА в) план удовлетворяющий области допустимых функции и целевой функции г) допустимый план, удовлетворяющий целевой функции. Определить в какой точке находится максимальное значение ЗЛП? АDCD – область допустимых значений. 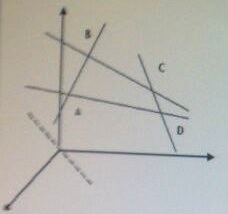 а) А ДА б) В в) С г) D Определить в какой точке находится максимальное значение ЗЛП решая графическим способом. 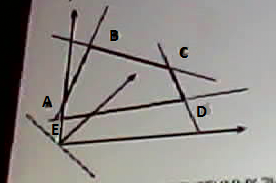 ABCDE – область допустимых значений. а) А б) B в) С ДА г) D д) E Определите разрешающий элемент в следующей симплексной таблице при решении задачи максимизации:
Определить будет ли данный план опорным, если нет, то почему: Изображена таблица а) будет НЕТ б) не будет, т.к. не все клетки заполнены в) не будет, т.к. не выполняется условие m+n-1 НЕТ г) не будет, т.к. для некоторых занятых клеток … Особенностью задач динамического программирования заключается в том, что: дальнейшее состояние экономической системы зависит только от данного состояния и не зависит от предыстории данного состояния Основные функциональные уравнения задачи оптимального распределения капиталовложений имеют: а) fN(c) = qN(c) fn(c) = max {qn (x) + fn-1 (c-x)} ДА б) fN(c) = qN(c) fn(c) = min {qn (x) + fn-1 (c-x)} в) fN(c) = qN(c) fn(c) = min {qn (x) + fn-1 (х-с)} Оцените целесообразность включения в план нового вида продукции, нормы затрат ресурсов на единицу которого равны соответственно 3, 4, 2, а прибыль от реализации равна 40 ден.ед., если при решении задачи о производстве продукции при оптимальном использовании ресурсов было получено следующее решение
Оцените целесообразность закупки 10 единиц второго вида ресурса по цене 2,5 ден.ед., если при решении задачи о производстве продукции при оптимальном использовании ресурсов было получено следующее решение
Оптимальной стратегией замены оборудования для оборудования возраста 4 года является:
а) 1 год f5(4) –замена; 2 год f4(1) –сохранение; 3 год f3(0) –сохранение; 4 год f2(1) –сохранение; 5 год f1(2) –сохранение. ДА б) 1 год f1(4) –сохранение; 2 год f2(3) –замена; 3 год f3(1) –сохранение; 4 год f4(2) –сохранение; 5 год f5(3) –замена. НЕТ в) 1 год f5(4) –замена; 2 год f4(1) –сохранение; 3 год f3(2) –сохранение; 4 год f2(3) –замена; 5 год f1(1) –сохранение. г) 1 год f1(4) –сохранение; 2 год f2(3) –замена; 3 год f3(0) –сохранение; 4 год f4(1) –сохранение; 5 год f5(2) –сохранение. д) 1 год f5(4) –замена; 2 год f4(0) –сохранение; 3 год f3(1) –сохранение; 4 год f2(2) –сохранение; 5 год f1(3) –сохранение. При решении нелинейных задач командой Поиск решения Excel значение функции в начальной точке должно быть: отлично от нуля, так как на каждом шаге итерационного процесса решения задачи проверяется достижение оптимального решения по формуле ∆f=fk+1 – fk / fk ≤ ε – заданная величина точности решения, а на нуль делить нельзя При решении задачи динамического программирования: а) она разбивается на шаги и процесс решения является ассоциативным; б) строится характеристический многочлен; в) процесс решения не является многошаговым; г) она разбивается на шаги и нумерация шагов (этапов) осуществляется от конечного этапа к начальному; (ДА) д) необходимо сложить значения переменных для каждого этапа. При решении задачи транспортного типа на максимум были получены оценки свободных клеток В=1,0 следовательно: Задача имеет …..ственное оптимальное решение ДА План находящийся в данной таблице является
По данному опорному плану определить транспортные расходы:
а) 215 ДА б) 230 в) 200 г) 254 д) 190 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

 у1 + 3 у2 – 4у3
у1 + 3 у2 – 4у3  у1 + 5 у2 + 4у3
у1 + 5 у2 + 4у3  у1 + 5 у2 + 4у3
у1 + 5 у2 + 4у3  у1 + 3 у2 - 4у3
у1 + 3 у2 - 4у3