Мат. анализ Сафронова А.А. ИПЗ. Решение Необходимое условие экстремума функции одной переменной. Уравнение f' 0

• Название: Решение Необходимое условие экстремума функции одной переменной. Уравнение f' 0
• Дата: 27.06.2021
• Размер: 142.28 Kb.
• Имя файла: Мат. анализ Сафронова А.А. ИПЗ.docx
• Тип: Решение; #221876

Российский государственный социальный университет

ИТОГОВОЕ ПРАКТИЧЕСКОЕ ЗАДАНИЕ

по дисциплине «Математический анализ»

ФИО студента	Сафронова Александра Александровна
Направление подготовки	Бизнес - информатика
Группа	БИЗ-Б-01-3-2020-1_ДИСТАНТ

Москва 2021

ВАРИАНТ 3

3)

Решение:

Необходимое условие экстремума функции одной переменной.
Уравнение f'₀(x*) = 0 - это необходимое условие экстремума функции одной переменной, т.е. в точке x* первая производная функции должна обращаться в нуль. Оно выделяет стационарные точки x_с, в которых функция не возрастает и не убывает.
Достаточное условие экстремума функции одной переменной.
Пусть f₀(x) дважды дифференцируемая по x, принадлежащему множеству D. Если в точке x* выполняется условие:
f'₀(x*) = 0
f''₀(x*) > 0
то точка x* является точкой локального (глобального) минимума функции.
Если в точке x* выполняется условие:
f'₀(x*) = 0
f''₀(x*) < 0
то точка x* - локальный (глобальный) максимум.
Решение.
Находим первую производную функции:

или

Приравниваем ее к нулю:

x₁ = -1
x₂ = -3
Вычисляем значения функции
f(-1) = 2
f(-3) = 6
Ответ:
f_min = 2, f_max = 6
Используем достаточное условие экстремума функции одной переменной. Найдем вторую производную:

или

Вычисляем:
y''(-1) = -2<0 - значит точка x = -1 точка максимума функции.
y''(-3) = 2>0 - значит точка x = -3 точка минимума функции.

) Область определения функции. Точки разрыва функции.
2) Четность или нечетность функции.

Функция общего вида
3) Периодичность функции.
4) Точки пересечения кривой с осями координат.
Пересечение с осью 0Y

Пересечение с осью 0X
y=0


5) Исследование на экстремум.
y = (3-x^2)/(x+2)
Найдем точки разрыва функции.
x₁ = -2
1. Находим интервалы возрастания и убывания. Первая производная.

или

Находим нули функции. Для этого приравниваем производную к нулю
-x²-4·x-3 = 0
Откуда:
x₁ = -1
x₂ = -3

(-∞ ;-3)	(-3; -2)	(-2; -1)	(-1; +∞)
f'(x) < 0	f'(x) > 0	f'(x) > 0	f'(x) < 0
функция убывает	функция возрастает	функция возрастает	функция убывает

В окрестности точки x = -3 производная функции меняет знак с (-) на (+). Следовательно, точка x = -3 - точка минимума. В окрестности точки x = -1 производная функции меняет знак с (+) на (-). Следовательно, точка x = -1 - точка максимума.
2. Найдем интервалы выпуклости и вогнутости функции. Вторая производная.

или

Находим корни уравнения. Для этого полученную функцию приравняем к нулю.

Для данного уравнения корней нет.

(-∞ ;-2)	(-2; +∞)
f''(x) > 0	f''(x) < 0
функция вогнута	функция выпукла

6) Асимптоты кривой.

Уравнения наклонных асимптот обычно ищут в виде y = kx + b. По определению асимптоты:

Находим коэффициент k:


Находим коэффициент b:


Получаем уравнение наклонной асимптоты:
y = -x+2
Найдем вертикальные асимптоты. Для этого определим точки разрыва:
x₁ = -2
Находим переделы в точке x=-2


x₁ = -2 - точка разрыва II рода и является вертикальной асимптотой.

Найдем наклонную асимптоту при x → -∞:

Находим коэффициент k:


Находим коэффициент b:


Получаем уравнение наклонной асимптоты:
y = -x+2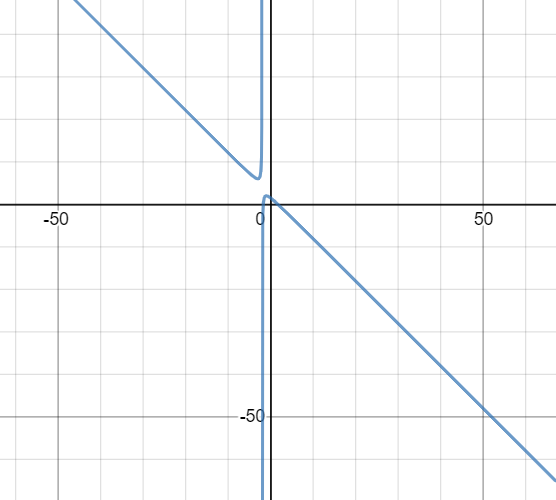