В транспортной задаче оптимальный план будет не единственный если
 Скачать 2.94 Mb.
|
После приведения математической модели задачи линейной оптимизации к каноническому виду мы получаем:F = 6x1 -3x2 +7x3 (min) 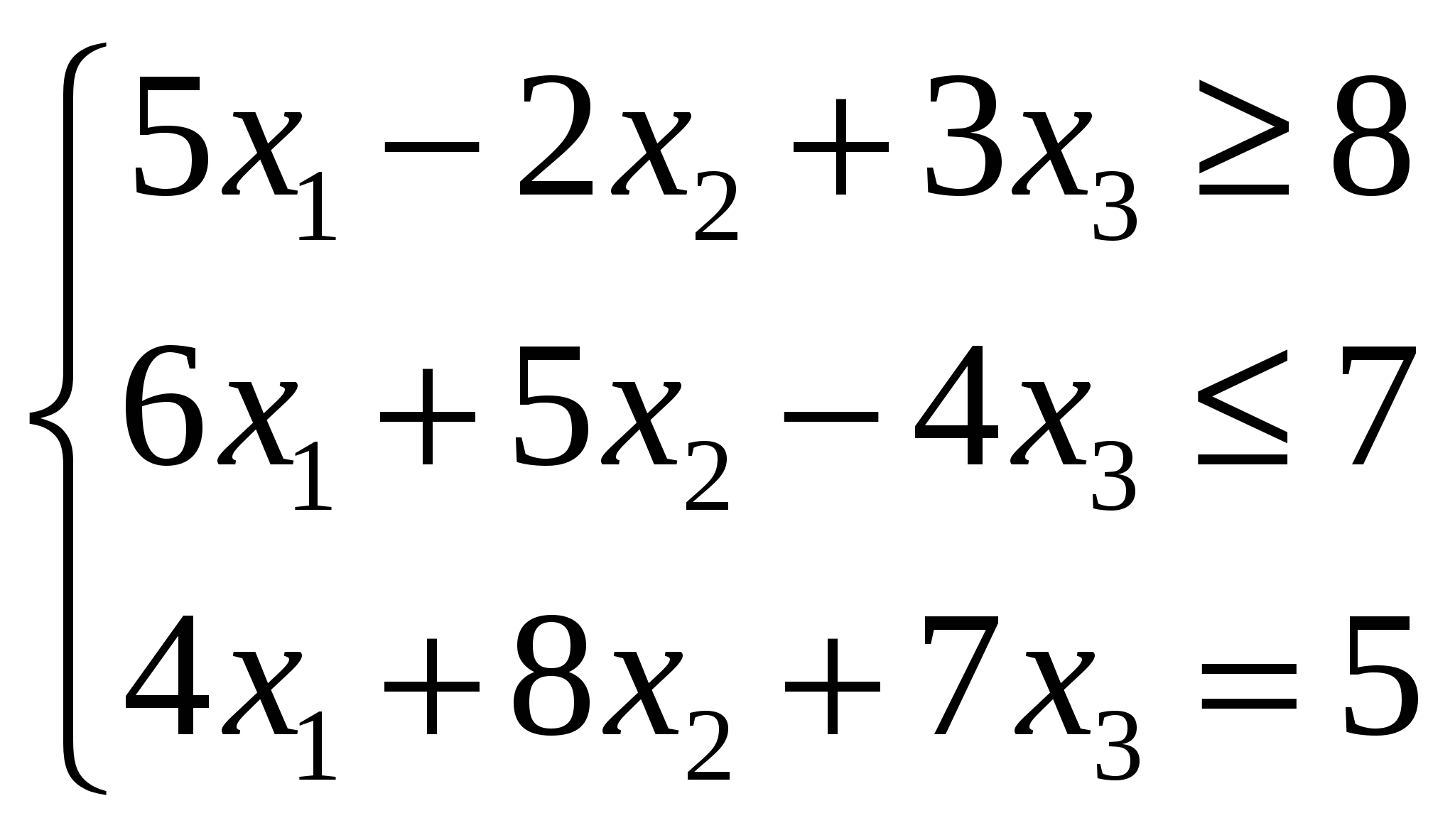 x1≥0, x3≥0
Переход к нехудшему опорному решению транспортной задачи можно осуществить: а) методом потенциалов; б) методом северо-западного угла; в) методом наименьших квадратов; г) методом функциональных уравнений. Принцип оптимальности Беллмана для задачи в которой решается вопрос о том, как спланировать работу группы предприятий, чтобы экономический эффект от выделенных этим предприятиям дополнительных финансовых или материальных ресурсов был максимальным, формализуется в следующее функциональное уравнение динамического программирования.
При решении пары двойственных задач (одна из которых задача об оптимальном использовании ресурсов) получен следующий результат: f(  ) = 20x1+10x2+9x3 (max);  =(10; 0; 3; 0; 8; 0);  =(2; 0; 4; 0; 5; 0). Значение прибыли, если в производство ввести 3 единицы наиболее дефицитного ресурса, будет равно
Полученный план перевозок транспортной задачи является
После пересчета элементов данной таблицы задачи максимизации линейного программирования
мы приходим к следующей таблице
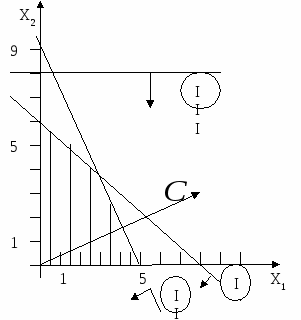
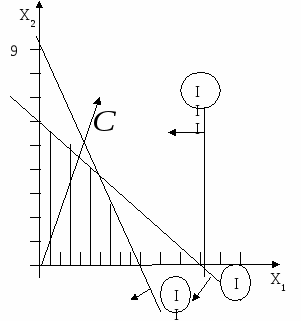
При решении данной задачи линейного программирования графическим методом получаем следующую иллюстрацию F= 8x1 +3x2 (max) 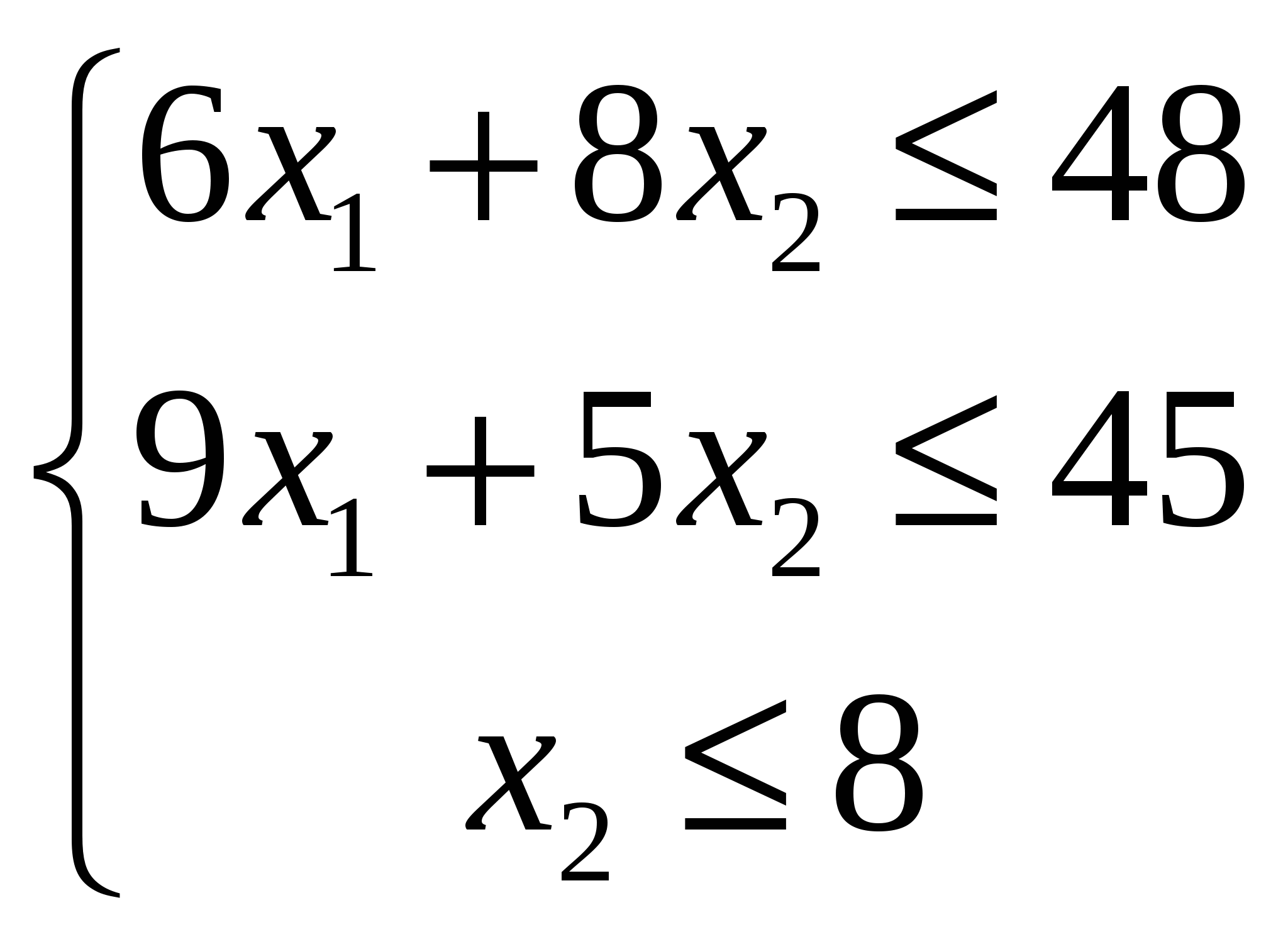 x1≥0, x2≥0
Признаком бесконечности множества оптимальных планов является: а) наличие в f-строке симплексной таблицы, содержащей оптимальный план хотя бы одного нулевого элемента; б) наличие в f-строке симплексной таблицы, содержащей оптимальный план хотя бы одного отрицательно элемента, которому соответствует столбец неположительных элементов; в) наличие в f-строке симплексной таблицы, содержащей опорный план хотя бы одного нулевого элемента; Признаком оптимальности при решении задачи максимизации линейного программирования симплексным методом является: а) неотрицательность элементов столбца свободных членов; б) неотрицательность элементов f-строки; в) неположительность элементов f-строки. Предметом математического программирования является: а) любой класс задач; б) класс экстремальных задач; в) класс задач на экстремум (максимум или минимум) функции со многими неизвестными и системой ограничений на область изменения этих неизвестных. Пусть дана симптоматическая таблица. Определить элемент расположения в F строке в последнем столбце следующей симптоматической таблицы.
а) -6 б) 12 в) 6 г) 8 Пусть дана симплексная таблица с максимизацией целевой функции. Определить элемент расположенный во второй строке в последнем столбце следующей симплексной таблицы.
а) 1 б) 1 ДА в) 3/2 г) 1/3 Пусть дана симплексная таблица с максимизацией целевой функции …….
а) 2 б) 6 НЕТ в) 3 г) 8 Переменные в математической модели, описывающей состояние экономической системы, могут быть: все перечисленные в п.п. А-Д. \ Предметом «Исследования операций в экономике» является: разработка и исследование методов наиболее эффективного управления экономическими системами Привести модель ЗЛП к каноническому виду: F 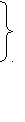 (x) = 3X1+2X2+X3+4X4 (max) Х1+3Х2-5Х3+Х4 ≥9 5Х1-Х2-3Х3 = 6 -Х1+4Х2+2Х3-Х4 ≤4 Х1≥0 (i=1,4) F 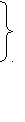(x) = 3X1+2X2+X3+4X4 (max) Х1+3Х2-5Х3+Х4-Х5=9 5Х1-Х2-3Х3=6 -Х1+4Х2+2Х3-Х4+Х5=4 Х1≥0 (i=1,4) ДА | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
)
) -7x3 (max)
), x
≥0, 
)
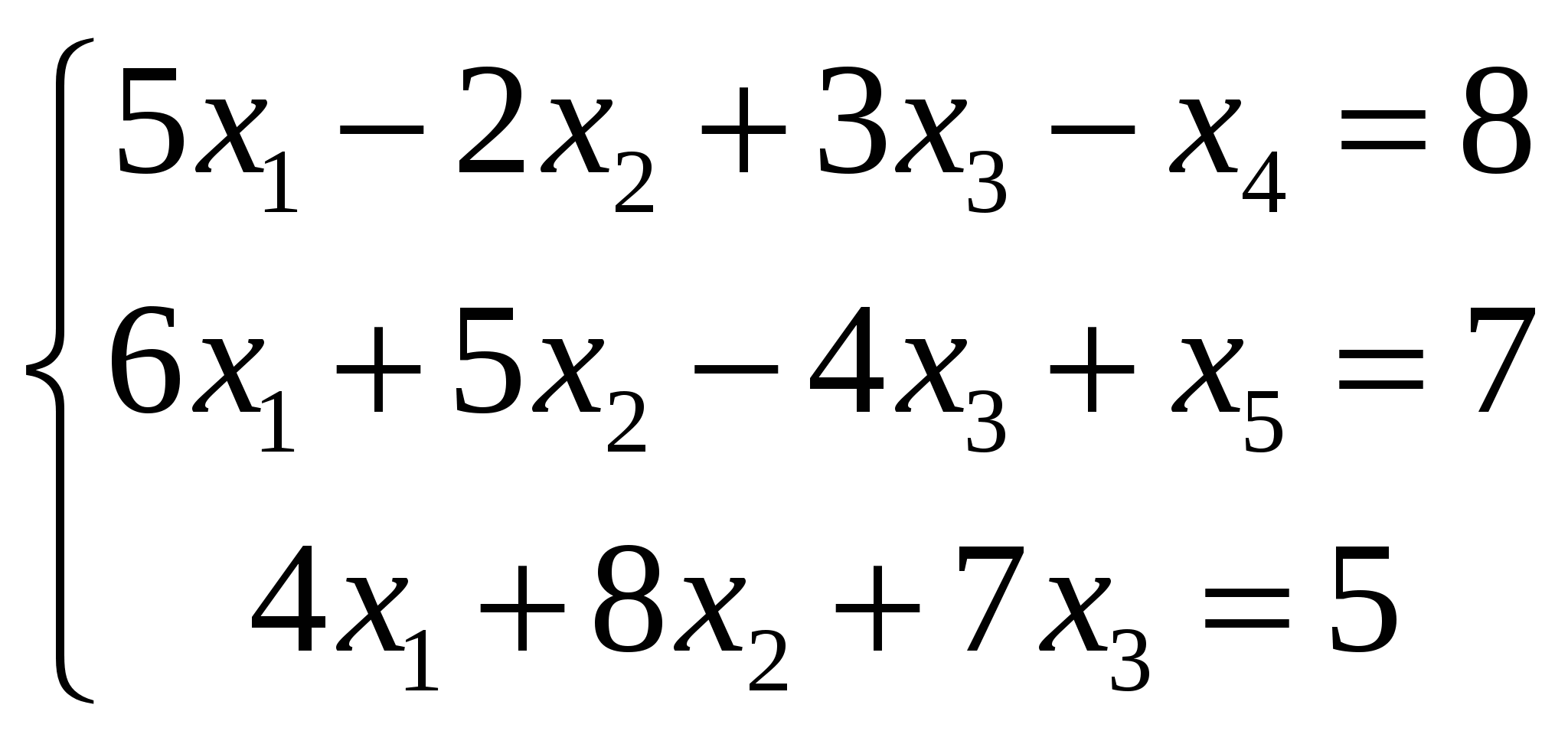
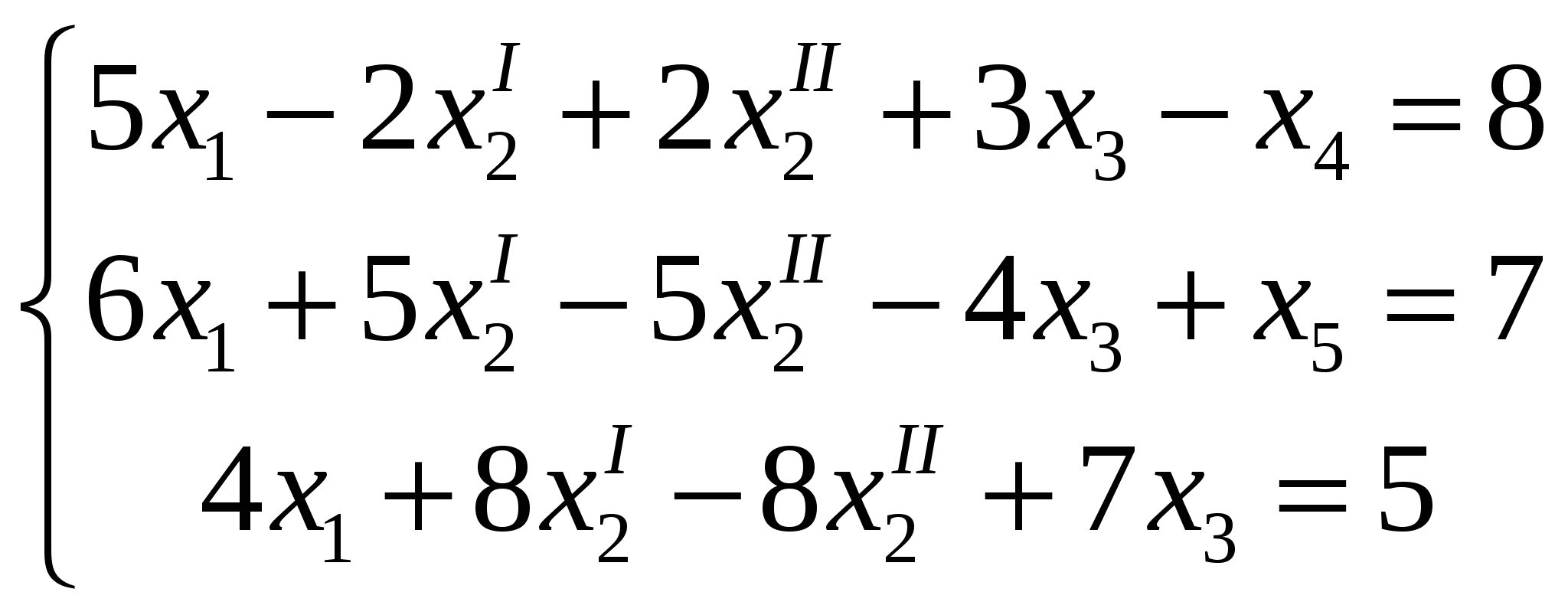
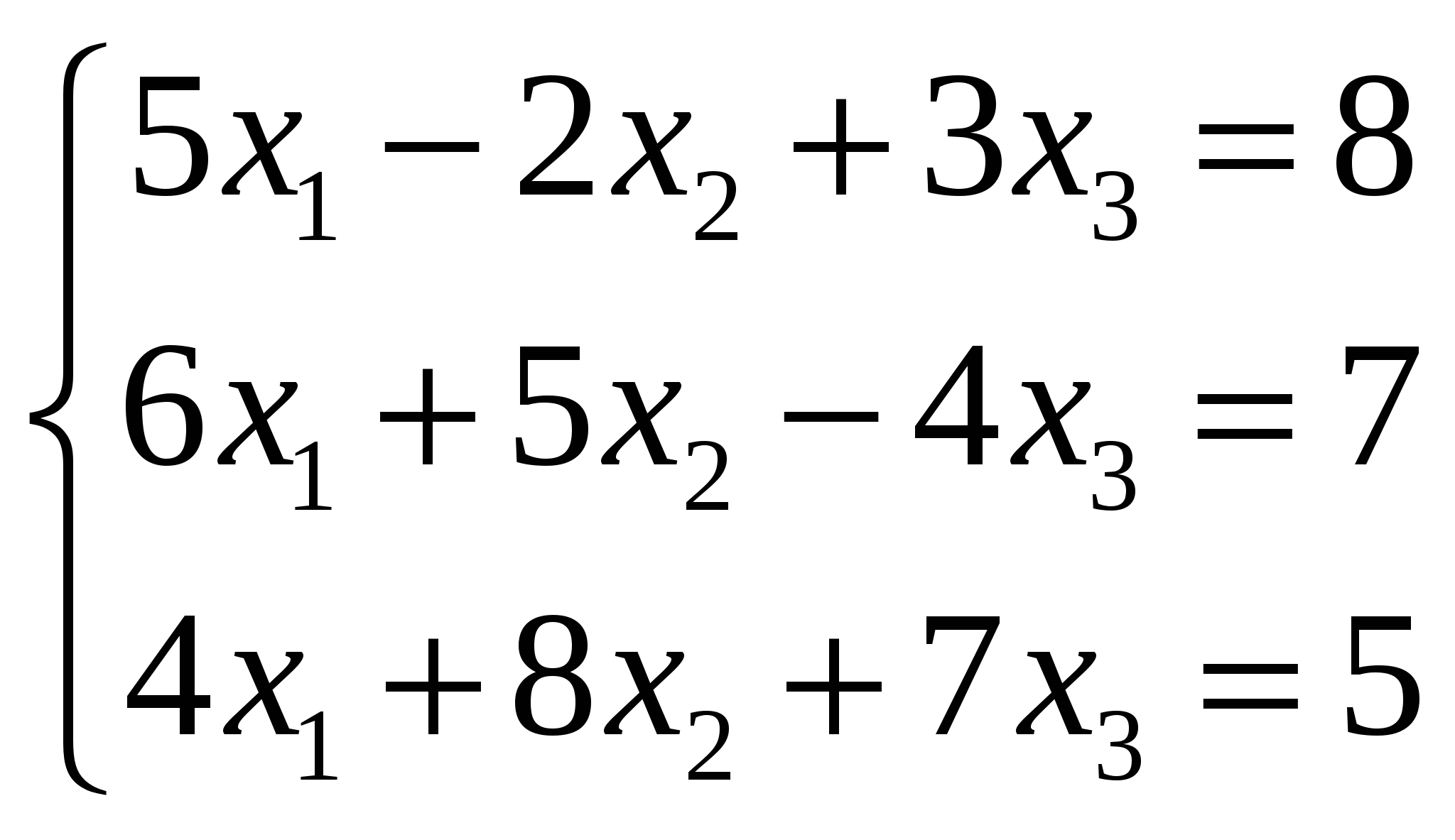
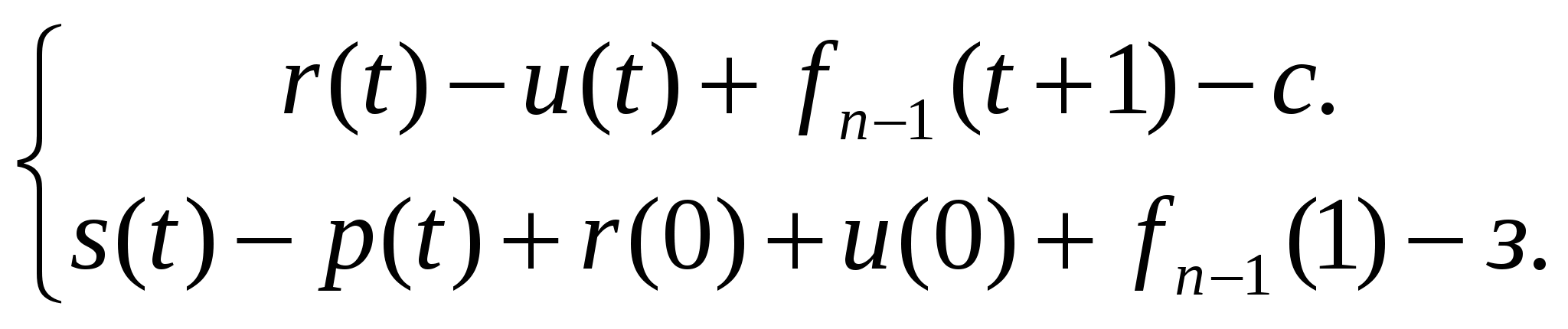
(ДА)
) (ДА)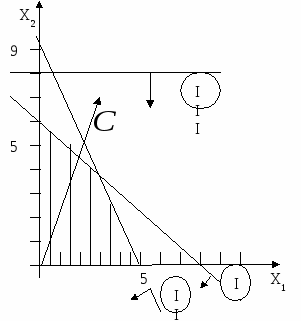
) 
) 
)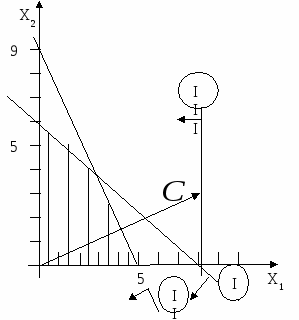