Лабораторная работа 6. Постановка задачи для заданных значений p и q
 Скачать 53.39 Kb. Скачать 53.39 Kb.
|
|
Вариант № 22 p=2 q=2 Постановка задачи для заданных значений p и q Запишем заданную систему уравнений для p=2 q=2: 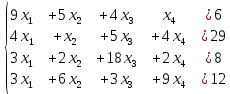 Матрица системы и столбец свободных членов имеют вид: A= 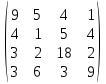 B= B=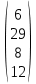 Найти решение получившейся СЛАУ с использованием метода Крамера. Вычисляем определитель матрицы А: detA= 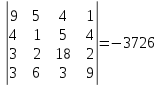 Формируем вспомогательные матрицы A A An , , ..., 1 2 , которые получаются из матрицы А путём замены i-го столбца на столбец свободных членов В 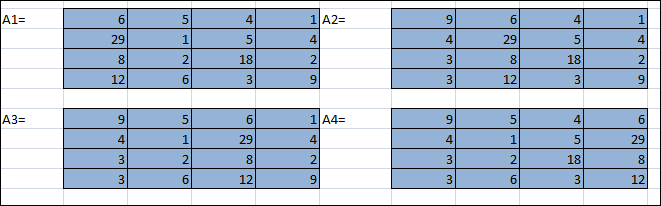 Вычисляем последовательно определители для получившихся матриц: 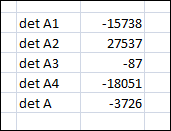 Находим значения неизвестных xi 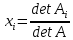 , i= , i=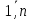 При использовании метода понадобится функция: МОПРЕД(арг), которая вычисляет определитель матрицы, подставленной в качестве аргумента. 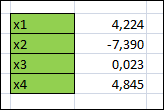 Описание решения задачи с использованием матричного метода. Этот метод основан на использовании обратных матриц. Он может быть применён только в том случае, если det A0 . Воспользуемся записью СЛАУ в матричной форме : AX= B A= 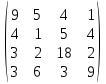 B= B=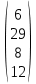 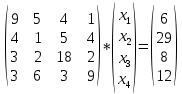 Если 0det A , то существует обратная матрица A-1 Найдем обратную матрицу при помощи функции МОБР(арг) 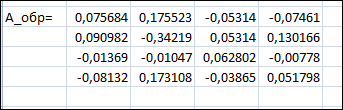 Найдем значения переменных при помощи функции МУМНОЖ(арг1;арг2) 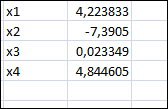 Описание решения задачи с использованием метода Гаусса Этот метод является наиболее распространённым методом решения СЛАУ. В его основе лежит идея последовательного исключения неизвестных. Универсальность метода обусловлена возможностью поиска решения с его использованием в случае, когда система имеет единственное решение или множество решений. Существуют различные схемы вычисления решения по этому методу. Рассмотрим подробно схему единственного деления. Разделим первое уравнение системы на a11 и вычитаем из первого уравнения полученное умноженное на а21, получим 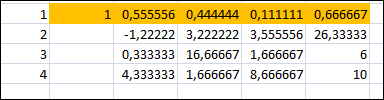 Далее аналогичным образом продолжаем вычисления до тех пор пока не придем к уравнению с одной переменной 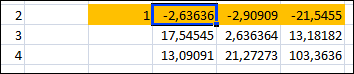  Находим значение переменных 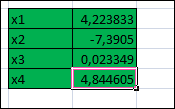 Выводы На основе выполненной лабораторной работы можно сделать следующие выводы: Решение систем линейных алгебраических уравнений в MS EXCEL значительно облегчают поиск значений, но не каждый метод можно реализовать. |
