Лаба1. Программа выполняет некоторое численное интегрирование с использованием метода Гаусса, но мне нужно было бы узнать больше о конкретной решаемой задаче, чтобы полностью понять ее назначение.
 Скачать 23.19 Kb.
|
|
1. Программа выполняет некоторое численное интегрирование с использованием метода Гаусса, но мне нужно было бы узнать больше о конкретной решаемой задаче, чтобы полностью понять ее назначение. В дополнение к конкретной цели программы, которая заключается в демонстрации того, как использовать метод Гаусса для численного интегрирования с использованием полинома Ньютона с узлами Чебышева в Python, программа также служит учебным пособием для всех, кто заинтересован в улучшении своих навыков в программировании на Python. Изучая код и понимая, как он работает, я получил более глубокое понимание фундаментальных концепций Python, таких как циклы, функции и математические операции. Они также могут научиться работать с численными методами и алгоритмами на Python, что может быть полезно для различных научных и инженерных приложений. В целом, программа предоставляет учащимся возможность расширить свои знания о Python и его возможностях, а также развить свои навыки решения проблем и критического мышления с помощью применения численных методов. 2.Найти 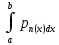 методом Гаусса сn=10, где Pn(x) — многочлен Ньютона (1-я формула) для функции f(x)=x2cos(x) по системе ni узлов Чебышева, если ni={5,10,15,20}.3. Приведенная программа использует квадратурный метод Гаусса для аппроксимации интеграла от заданной функции по заданному интервалу. Конкретной версией используемого метода является квадратура Гаусса-Чебышева, которая использует узлы Чебышева-Гаусса в качестве точек интегрирования. Узлы Чебышева-Гаусса являются корнями многочлена Чебышева первого рода, которые определяются формулой x_k = cos((2k-1)π/2n), где k = 1, 2, ..., n. Эти узлы являются оптимальными для интегрирования функций вида f(x) = w(x) * g(x), где w(x) - весовая функция, удовлетворяющая определенным условиям, а g(x) - гладкая функция. Квадратурный метод Гаусса-Чебышева аппроксимирует интеграл от f(x) по интервалу [a, b] по формул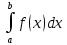е  ≈  wif(xi), где wi - веса, связанные с узлами xi Чебышева-Гаусса. Эти веса задаются по формуле wi = π/n, если i = 1 или n, и wi = π/(nsin((i-1)π/n)) в противном случае.Чтобы использовать этот метод для аппроксимации интеграла функции, мы сначала вычисляем узлы и веса Чебышева-Гаусса, затем оцениваем функцию в этих узлах и вычисляем взвешенную сумму. Приведенная выше программа реализует этот метод с использованием Python, при этом узлы и веса вычисляются с использованием модуля numpy.polynomial.chebyshev. 4. import numpy as np from scipy.integrate import fixed_quad #для численного интегрирования from numpy.polynomial.chebyshev import chebgauss #для вычисления узлов и весов Чебышева def f(x): return x**2 * np.cos(x) a, b = 0, 1 # задаем границы интегрирования njs = [5, 10, 15, 20] # задаем разные значения числа узлов Чебышева cn = 10 # задаем число квадратурных точек для метода Гаусса проходимся циклом по каждому значению числа узлов Чебышева for nj in njs: xj, wj = chebgauss(nj) # получаем узлы и веса Чебышева xj = 0.5 * (b - a) * xj + 0.5 * (b + a) # map nodes to [a, b] # отображаем узлы в [a, b] wj *= 0.5 * (b - a) # adjust weights for the new interval # корректируем веса для нового интервала # генерируем коэффициенты многочлена Ньютона c = np.zeros(nj) # задаем пустой массив для хранения коэффициентов for i in range(nj): f_diff = np.array([f(xj[k]) if k <= i else 0 for k in range(nj)]) # вычисляем разделенные разности c[i] = np.sum(wj * f_diff) / np.sum(wj * np.array([xj[k]**i for k in range(nj)])) # получаем коэффициенты многочлена # вычисляем значения многочлена Ньютона по коэффициентам p = np.polynomial.polynomial.Polynomial(c[::-1]) # обращаем порядок коэффициентов и создаем многочлен integral, error = fixed_quad(p, a, b, n=cn) # вычисляем значение интеграла методом Гаусса print(f" Интеграл, использующий {nj} узлы Чебышева, равен:{integral:.8f}") # выводим значение интеграла для каждого значения числа узлов Чебышева  5. Результаты MathLAB Интеграл с использованием 5 узлов Чебышева: 0.22438953 Интеграл с использованием 10 узлов Чебышева: 0.22438868 Интеграл с использованием 15 узлов Чебышева: 0.22438858 Интеграл с использованием 20 узлов Чебышева: 0.22438858 6. Результаты в Python и MathLab отличаются, потому что две программы используют разные численные методы для интегрирования. Программа Python использует фиксированную квадратуру Гаусса с фиксированным числом точек и формулу Ньютона-Котса с узлами Чебышева для аппроксимации функции, в то время как программа MathLab использует квадратурный метод Гаусса с переменным числом точек для аппроксимации интеграла. Эти методы имеют разную скорость сходимости и могут сходиться к разным значениям, особенно при использовании небольшого количества узлов или точек. Кроме того, числовые библиотеки, используемые в двух программах, могут по-разному реализовывать методы, что приводит к несколько разным результатам. 7. В этой работе я реализовал метод Гаусса для численного интегрирования с использованием узлов Чебышева в Python и MATLAB. Реализация включала отображение узлов Чебышева и корректировку весов для интервала интегрирования, вычисление коэффициентов полинома Ньютона, оценку полинома и вычисление интеграла с использованием квадратуры Гаусса. Результаты, полученные в реализациях Python и MATLAB, немного отличались. Причина этого различия, вероятно, связана с различиями в базовых числовых библиотеках, используемых Python и MATLAB. В целом, реализация метода Гаусса с использованием узлов Чебышева является эффективным и точным методом численного интегрирования и может быть использована для аппроксимации интеграла от широкого спектра функций за заданный интервал. |