|
|
лаб 1. Министерство цифрового развития, связи и
МАССОВЫХ КОММУНИКАЦИЙ РОССИЙСКОЙ ФЕДЕРАЦИИ
Федеральное государственное образовательное
бюджетное учреждение высшего образования
«Санкт-Петербургский государственный университет
телекоммуникаций им. проф. М.А. Бонч-Бруевича»
Кафедра Информационных Управляющих Систем
Лабораторная работа №1
«Массивы и матрицы в Scilab. Решение задач линейной алгебры»
Состав бригады:
Студенты гр. ИСТ-133
Усынин М.С
Скрипник А.С
Принял:
доцент кафедры ИУС СПбГУТ
Литвинов В.Л
Санкт-Петербург
2023
Теоретический материал
1.1
Для работы с множеством данных удобно использовать массивы. Например, можно создать массив для хранения числовых или символьных данных. В этом случае вместо создания переменной для хранения каждого данного достаточно создать один массив, где каждому элементу будет присвоен порядковый номер.
Таким образом, массив — множественный тип данных, состоящий из фиксированного числа элементов. Как и любой другой переменной, массиву должно быть присвоено имя. Переменную, представляющую собой просто список данных, называют одномерным массивом, или вектором.
Для доступа к данным, хранящимся в определенном элементе массива, необходимо указать имя массива и порядковый номер этого элемента, называемый индексом. Если возникает необходимость хранения данных в виде таблиц, в формате строк и столбцов, то необходимо использовать двумерные массивы (матрицы).
Для доступа к данным, хранящимся в таком массиве, необходимо указать имя массива и два индекса: первый должен соответствовать номеру строки, а второй — номеру столбца, в которых хранится необходимый элемент. Значение нижней границы индексации в Scilab равно единице. Индексы могут быть только целыми положительными числами.
1.2
Листинг 3.2. Определение вектора-строки
--> V=[1 2 3 4 5]
V =
1 2 3 4 5
--> W=[1.1,2.3,-0.1,5.88]
W =
1.1000 2.3000 -0.1000 5.8800
Элементы вектора-столбца вводятся через точку с запятой:
name=[x1; x2; ...; xn]
Пример ввода вектора-столбца:
Листинг 3.3. Определение вектора-столбца
--> X=[1;2;3]
X =
1
2
3
1.3
Для работы с матрицами и векторами в Scilab предусмотрены следующие
операции:
+ — сложение;
- — вычитание
’ — транспонирование
* — матричное умножение
* — умножение на число;
ˆ — возведение в степень
\ — левое деление
/ — правое деление
.* — поэлементное умножение матриц;
.ˆ — поэлементное возведение в степень;
.\ — поэлементное левое деление;
./ — поэлементное правое деление
1.4
linsolve(A,b) — решает систему линейных алгебраических уравнений вида
A · x −
b = 0.
Листинг 3.37. Пример использования функции linsolve
-->//Решение системы линейных уравнений
-->//{x1+2x2-7=0; x1+x2-6=0}.
-->//Свободные коэффициенты вводятся как вектор-столбец
-->//и с учетом знаков.
-->A=[1 2;1 1];b=[-7;-6];
-->x=linsolve(A,b)
x =
5.
1.
-->//Результатом операции A*x+b является вектор, достаточно
-->//близкий к нулю, это значит, что система решена верно.
-->A*x+b
ans =
1.0D-14 *
- 0.6217249
0.0888178
-->//Решение системы {x1+x2-1=0; x1+x2-3=0}
-->A=[1 1;1 1]; b=[-1;-3];
-->//Система не имеет решений:
-->linsolve(A,b)
WARNING:Conflicting linear constraints!
ans =
[]
-->//Решение системы {3x1-x2-1=0; 6x1-2x2-2=0}.
-->//В случае, когда система имеет бесконечное
-->//множество решений, SCILAB выдаст одно из них.
-->A=[3 -1;6 -2];
-->b=[-1;-2];
-->x=linsolve(A,b)
x =
0.3
- 0.1
-->//Проверка неверна
-->A*x+b
ans =
1.0D-15 *
- 0.1110223
- 0.2220446
1.5
inv(A) — вычисляет матрицу, обратную к A
Листинг 3.35. Использование функции inv
-->//Пример вычисления обратной матрицы.
-->A=[1 2 3 5;0 1 3 2;4 2 1 1;2 3 0 1];
-->inv(A)
ans =
! 0.0285714 - 0.1428571 0.3428571 - 0.2 !
! - 0.1428571 0.2142857 - 0.2142857 0.5 !
! - 0.2 0.5 0.1 - 0.1 !
! 0.3714286 - 0.3571429 - 0.0428571 - 0.1 !
-->//При умножении обратной матрицы на исходную,
-->//получилась матрица, близкая к единичной.
-->inv(A)*A
ans =
1. - 1.110D-16 0. 0.
0. 1. - 5.551D-17 5.551D-17
0. 0. 1. 1.388D-17
0. 0. 6.939D-17 1.
-->//При попытке обратить вырожденную матрицу
-->//(определитель равен или близок к нулю)
-->//пользователь получит сообщение об ошибке.
-->B=[1 2 3;1 4 5;1 6 7];
-->inv(B)
!--error 19
Problem is singular
1.6
det(M) — вычисляет определитель квадратной матрицы М;
Листинг 3.30. Использование функции det
-->M=[1 0 2;3 2 1;0 3 1];
-->det(M)
ans = 17.
-->Z=[1 2 2;0 1 3;2 4 4];
-->det(Z)
ans = 0.
Решение заданий
Вариант - 1
Задание 1.1. Решить систему линейных алгебраических уравнений, сделать проверку
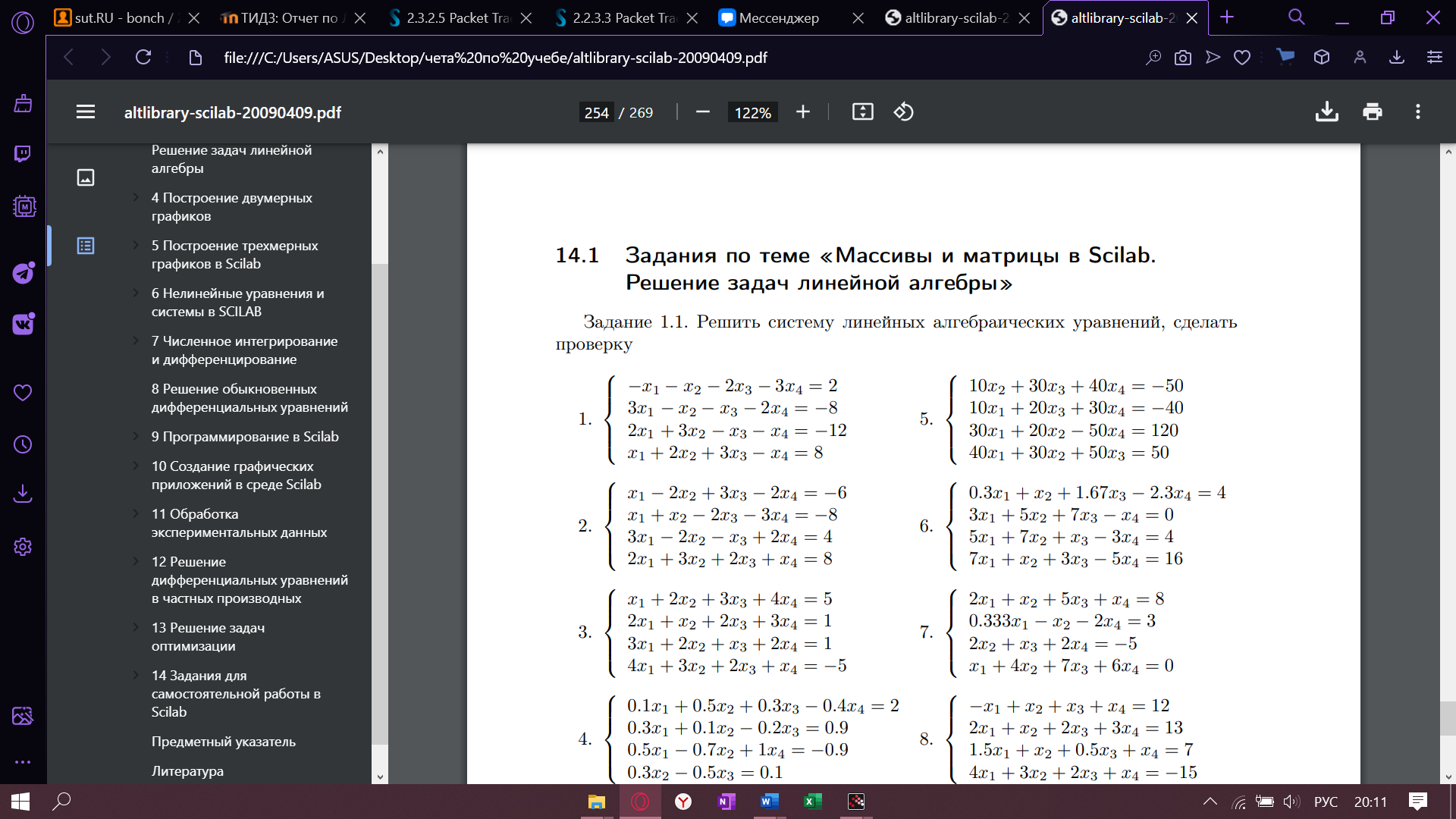
Листинг задания 1.1, Текст решения:
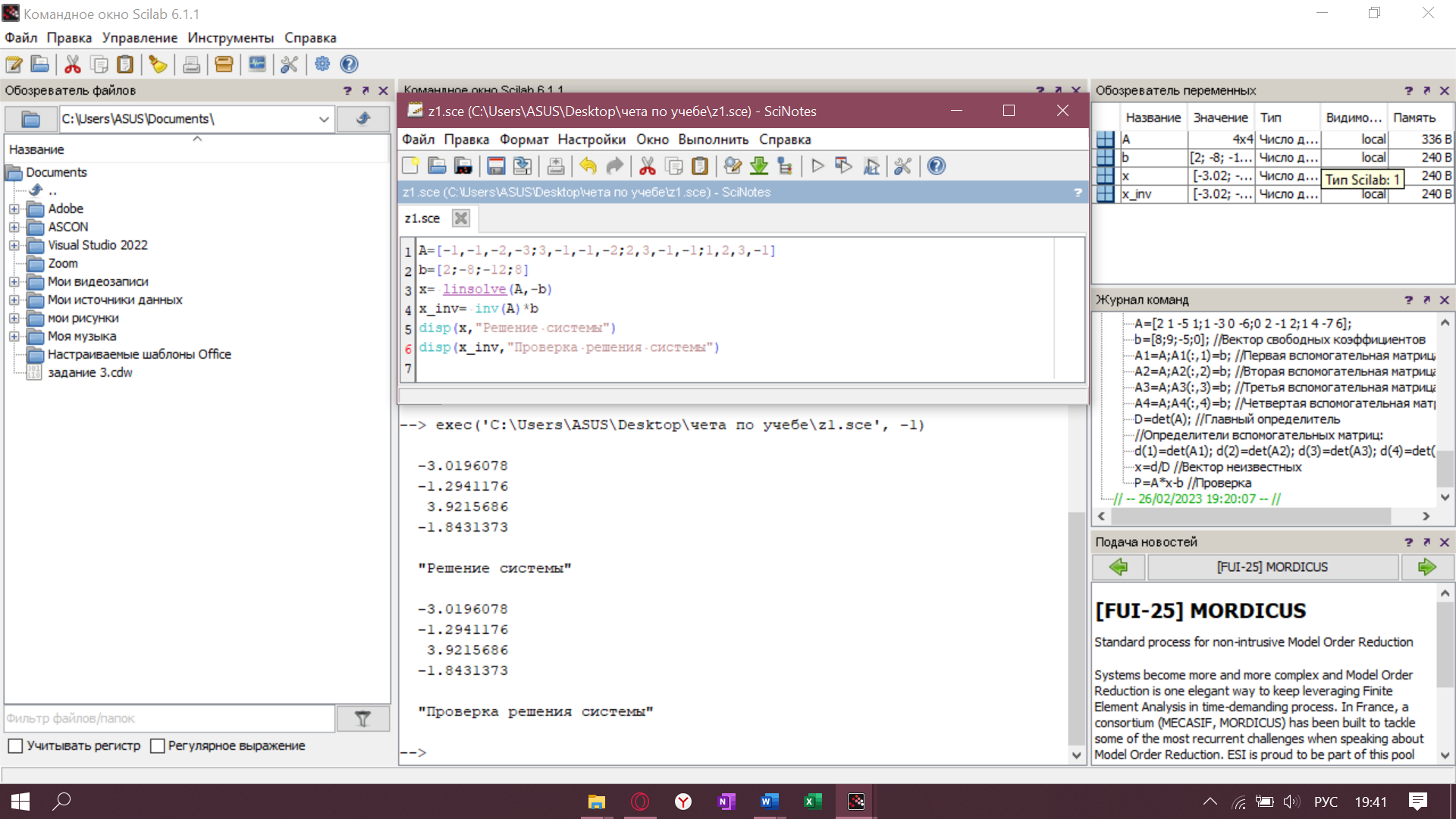
Результаты работы:
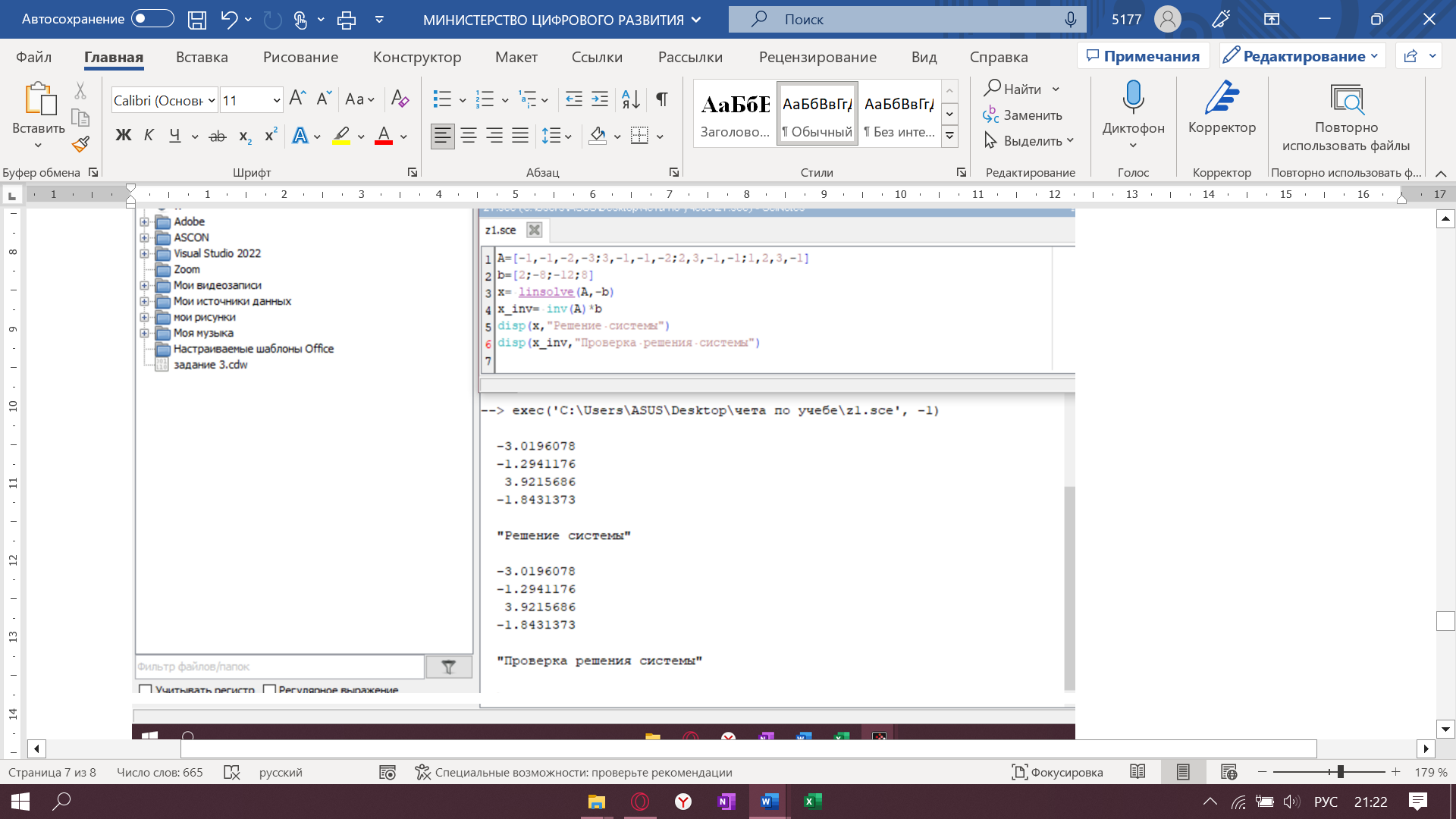
Задание 1.2. Если возможно, вычислить матрицу, обратную к матрице D.
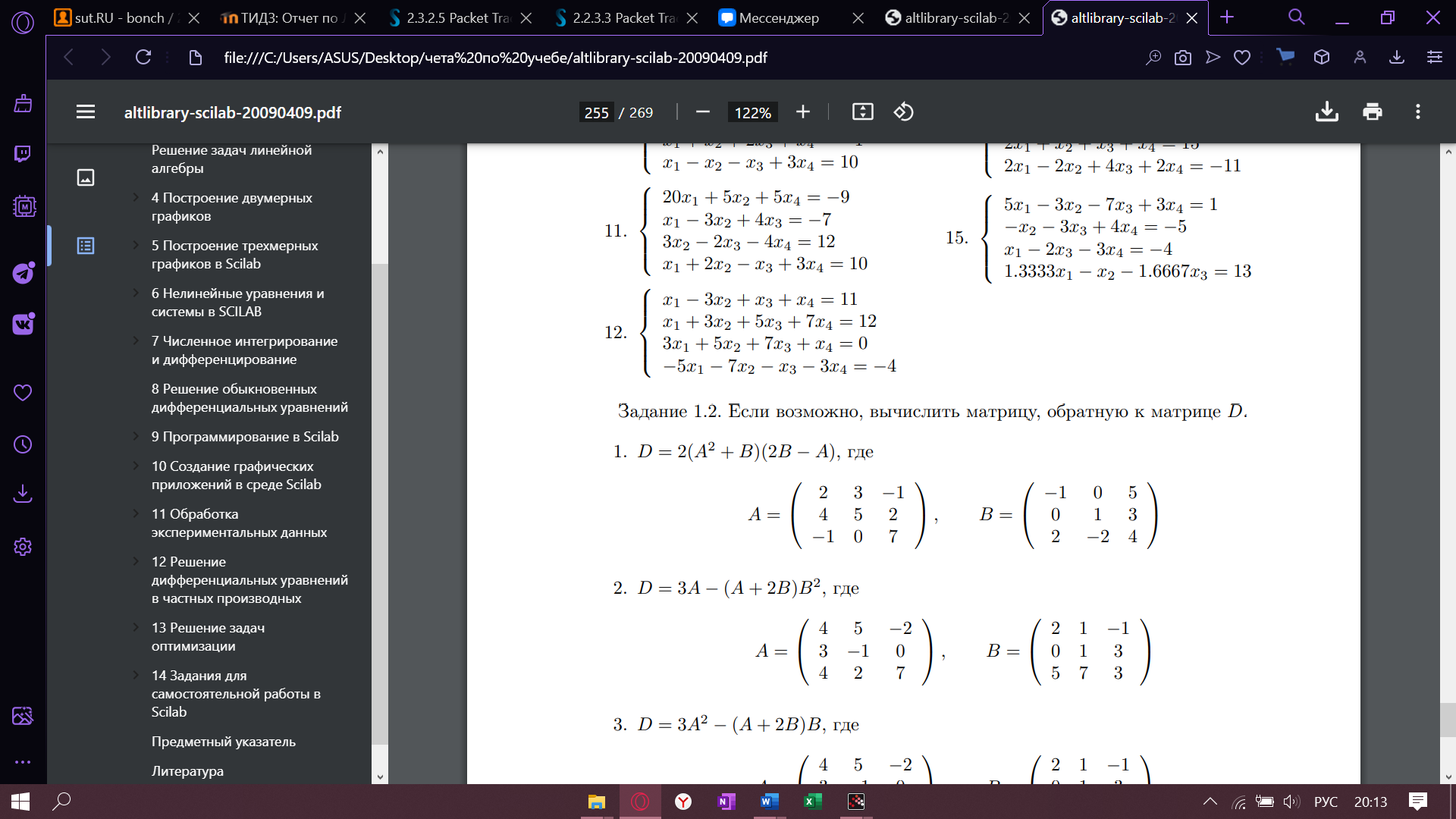
Листинг и результат 1.2:
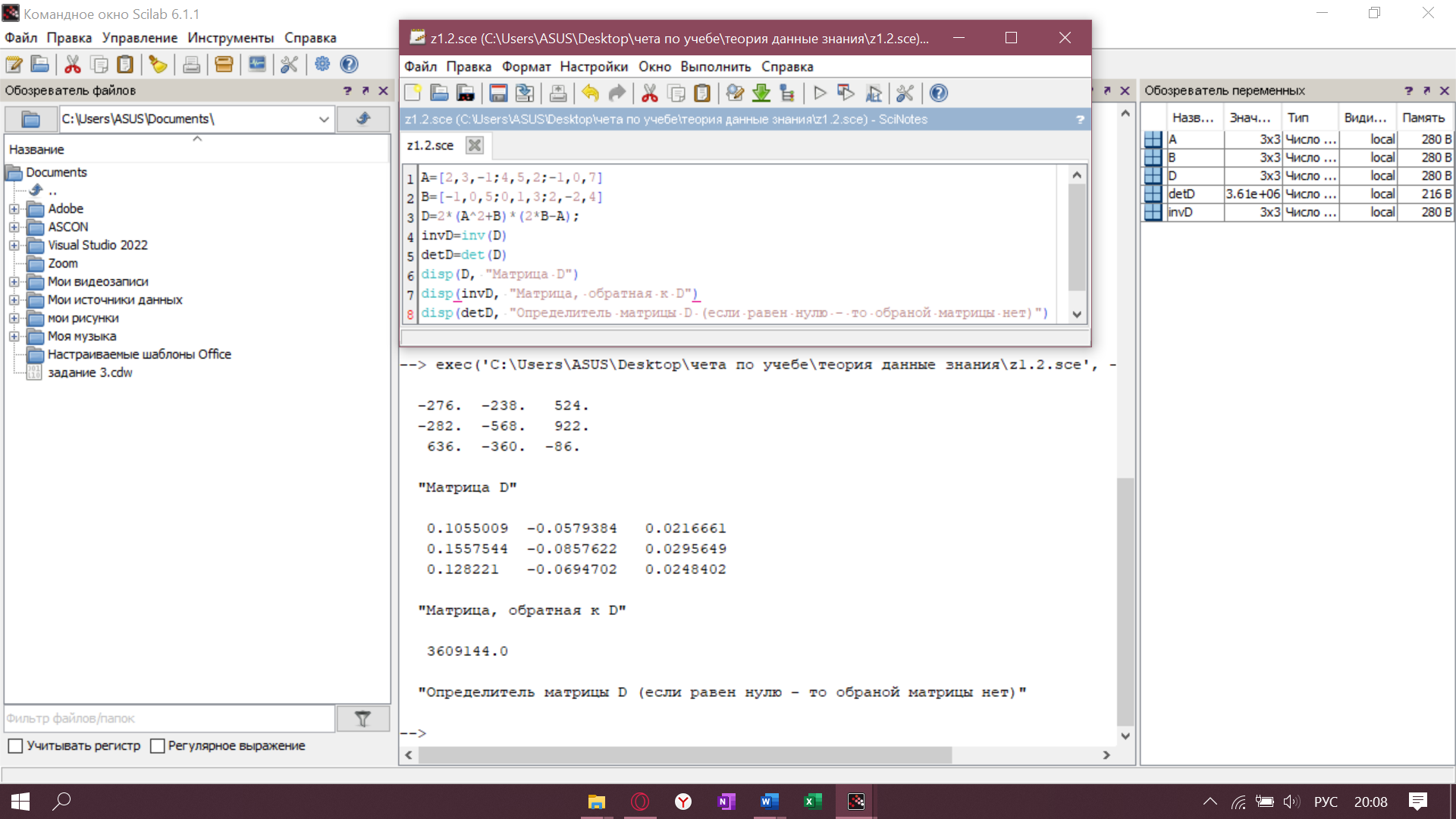
Вывод:
В задании 1.1 мы решили систему линейных алгебраических уравнений и сделали проверку, используя для получения решения linsolve(A,b) и inv(). Благодаря linsolve() мы решили систему уравнений, а использование inv() помогло нам найти обратную матрицу, что можно считать проверкой, т.к. значения в ответе совпали.
В задании 1.2 по возможности нужно было вычислить матрицу, обратную к матрице D. Чтобы понять возможно ли это вообще – нужно было найти определитель матрицы( с помощью det() ) , тк он у нас не равен нулю – обратная матрица существует. Тогда мы вычислили сначала саму матрицу D, а затем обратную к ней с помощью inv().
Описание матричных функций, использованных в выводе, можно найти в теоретическом материале. |
|
|
 Скачать 1.72 Mb.
Скачать 1.72 Mb.




