Бибиби. Praktika[1] - исправленное (1). Отчет по учебной (ознакомительной) практике студента 2 курса 242
 Скачать 314.21 Kb. Скачать 314.21 Kb.
|
|
МИНОБРНАУКИ РОССИИ Федеральное государственное бюджетное образовательное учреждение высшего образования «САРАТОВСКИЙ НАЦИОНАЛЬНЫЙ ИССЛЕДОВАТЕЛЬСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ИМЕНИ Н.Г. ЧЕРНЫШЕВСКОГО» Кафедра математической теории упругости и биомеханики ОТЧЕТ ПО УЧЕБНОЙ (ОЗНАКОМИТЕЛЬНОЙ) ПРАКТИКЕ
Руководитель практики
Саратов 2021 СОДЕРЖАНИЕ Введение 3 1 Вычисление пределов функций 4 2 Вычисление производной 6 3 Вычисление интегралов 8 4 Нахождение нулей полинома 9 5 Панель символьных вычислений. Упрощение выражений 10 6 Разложение в ряд Тейлора 12 Заключение 14 Список использованных источников 15 ВВЕДЕНИЕ Целью данной работы является знакомство с пакетом MathCAD и решение с его помощью математических задач по темам: вычисление пределов функций, вычисление производной, вычисление интегралов, нахождение нулей полинома, упрощение выражений и разложение в ряд Тейлора. Задачи взяты из книги Б. П. Демидовича «Сборник задач и упражнений по математическому анализу» и книги М. И. Сканави «Сборник конкурсных задач по математике для поступающих во втузы». 1 Вычисление пределов функций Пакет MathCAD позволяет вычислять пределы функций одной переменной и повторные пределы для функций многих переменных. Рассмотрим возможность решения пределов на примере № 420 и № 3181. Для вычисления пределов в Mathcad необходимо выполнить следующие действия: На математической панели выбрать кнопку Calculus Toolbar, откроется панель Calculus. На панели есть три оператора вычисления пределов, необходимо выбрать один из них (предел справа, слева или простой предел). Ввести выражение в поле ввода справа от lim. Под lim ввести имя переменной, по которой надо вычислить предел, и ее предельное значение. Выделить уголком или черным цветом все выражение целиком. В главном меню Mathcad выбрать Symbolics / Evaluate / Symbolically. Mathcad возвращает значение предела, если оно существует. Для повторных пределов необходимо в поле ввода справа от введённого lim ввести ещё один lim, следуя указанным выше шагам. Пример 1. Вычислим предел №420 из книги «Сборник задач и упражнений по математическому анализу» (рисунок 1). 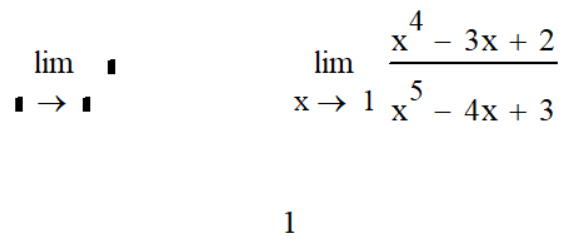 Рисунок 1 - Вычисление предела №420 Пример 2. Вычислим предел №3183 из книги «Сборник задач и упражнений по математическому анализу» (рисунок 2). 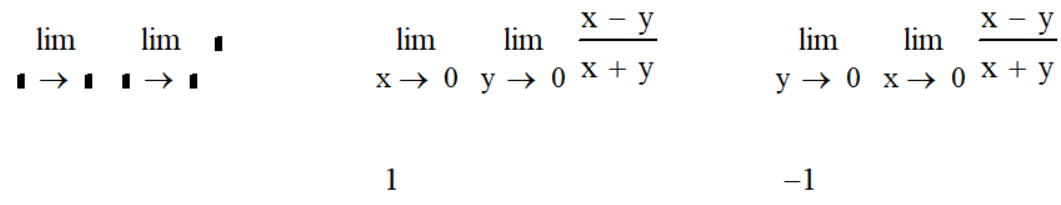 Рисунок 2 - Вычисление предела №3183 2 Вычисление производной Чтобы аналитически продифференцировать выражение по некоторой переменной, достаточно выделить в нем эту переменную и выбрать команду Symbolics / Variable / Differentiate. В результате в следующей строке за выражением появится значение ее производной. Пример 3. Продифференцируем функцию №852 из книги «Сборник задач и упражнений по математическому анализу» (рисунок 3). 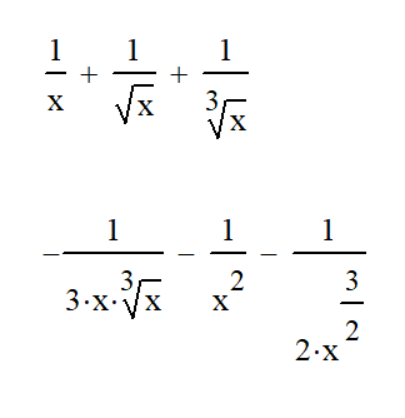 Рисунок 3 - Дифференцирование функции №852 Для того чтобы найти вторую производную, необходимо повторно выполнить эту последовательность действий, но уже к полученному результату дифференцирования. Так же находятся и производные высших порядков. Пример 4. Дважды продифференцируем функцию №1111 из книги «Сборник задач и упражнений по математическому анализу» (рисунки 4 и 5). 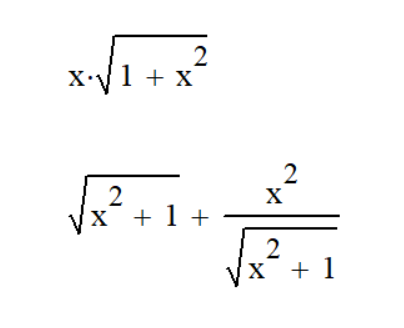 Рисунок 4 - Первая производная функции №1111 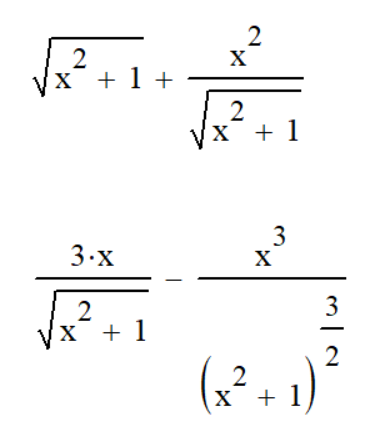 Рисунок 5 - Вторая производная функции №1111 3 Вычисление интегралов С помощью Mathcad мы можем вычислять неопределённые и определённые интегралы. Для этого необходимо на панели Calculus выбрать знак необходимого интеграла и записать с его помощью нужное выражение. Для вычисления неопределённого интеграла можно воспользоваться другим способом: выделить в выражении переменную и выполнить команду Symbolics / Variable / Integrate. Пример 5. Вычислим неопределённый интеграл №1647 из книги «Сборник задач и упражнений по математическому анализу» (рисунок 6). 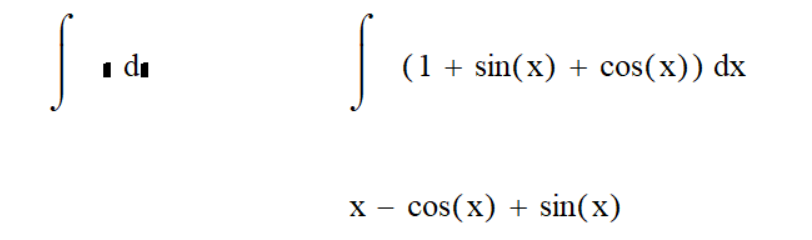 Рисунок 6 - Интегрирование функции №1647 Пример 6. Вычислим определённый интеграл №2209 из книги «Сборник задач и упражнений по математическому анализу» (рисунок 7). 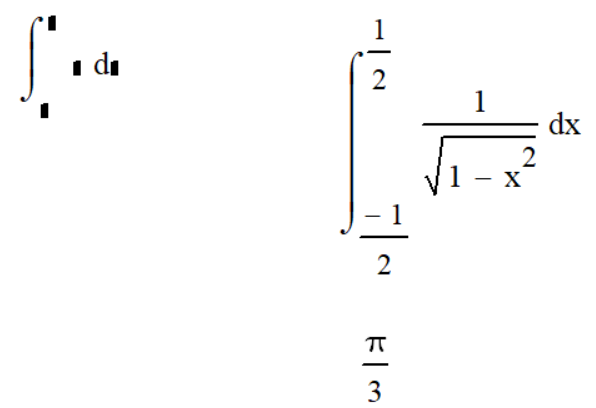 Рисунок 7 - Интегрирование функции №2209 4 Нахождение нулей полинома Если выражение представляет собой полином, то можно найти все его нули, использовав функцию polyroots, имеющую в качестве аргумента вектор коэффициентов полинома и возвращающую его нули. Для получения нулей полинома необходимо: Написать сам полином и приравнять его нулю. Создать функцию и приравнять её полиному с помощью знака «:=» (находится на панели Evaluation). Создать матрицу коэффициентов полинома (функция coeffs находится в Symbolic Keyword Toolbar). С помощью команды polyroots получить нули полинома (Insert / Function / polyroots). Пример 7. Найдём нули полнома x3-x2-17x-15 (рисунок 8). 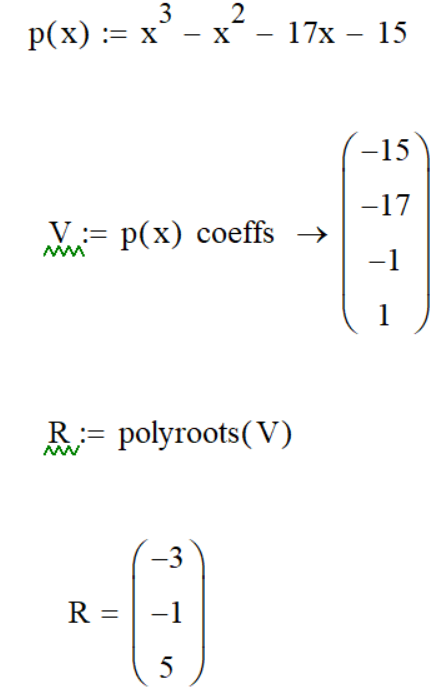 Рисунок 8 - Нахождение нулей полинома 5 Панель символьных вычислений. Упрощение выражений Символьные вычисления в MathCAD можно осуществлять в двух различных вариантах: команд строки меню Symbolics; оператора символьного вывода «→» и команд символьного процессора, которые вводятся с панели инструментов Symbolic. Первый способ более удобен тогда, когда требуется быстро получить какой-либо аналитический результат для однократного использования, не сохраняя сам ход вычислений. Второй способ более нагляден, так как позволяет записывать выражения в традиционной математической форме и сохранять символьные вычисления в документах MathCAD. Упрощение выражения – наиболее часто применяемая операция. Символьный процессор MathCAD стремится преобразовать выражением, чтобы оно приобрело более простую форму. При этом используются различные арифметические формулы, приведение подобных слагаемых, тригонометрические тождества, пересчет обратных функций и др. Упрощение выражений выполняется: с помощью команды меню Symbolics / Simplify; при помощи оператора символьного вывода с ключевым словом simplify (при этом необходимо учитывать, что если некоторым переменным, входящим в выражение, ранее были присвоены некоторые значения, то они будут подставлены в него при выполнении символьного вывода). Пример 8. Упростим выражение №2.074 из книги «Сборник конкурсных задач по математике для поступающих во втузы» обоими способами, приведёнными выше (рисунки 9 и 10). 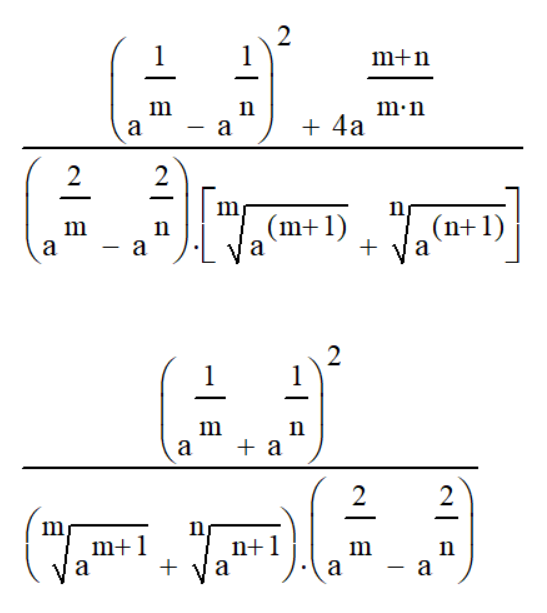 Рисунок 9 - Упрощение выражения №2.074 первым способом 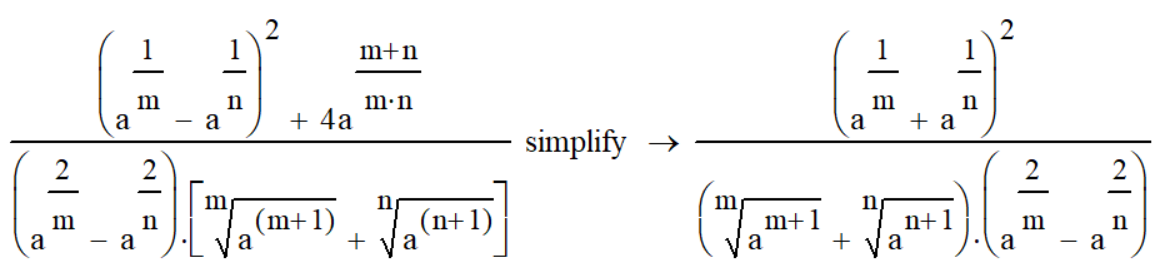 Рисунок 10 - Упрощение выражения №2.074 вторым способом Чтобы получить результат в «максимально упрощенном виде» (насколько это возможно в MathCAD), следует вместе с ключевым словом simplify использовать модификатор max. Пример 9. Упростим выражение из предыдущего номера с помощью модификатора max (рисунок 11). 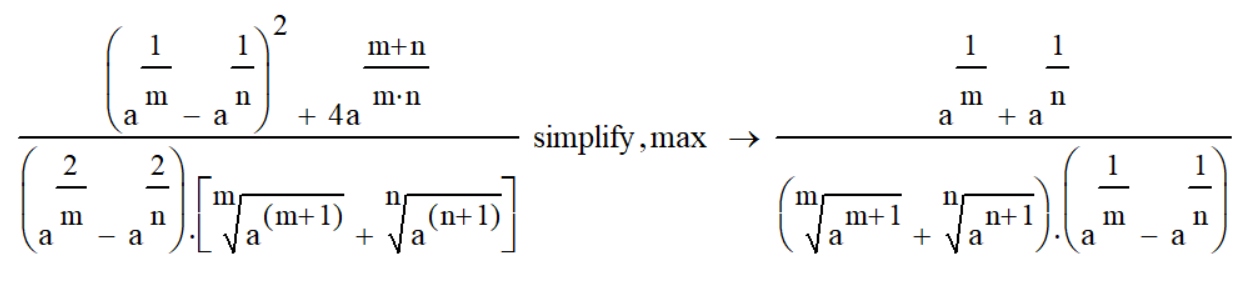 Рисунок 11 - Упрощение выражения №2.074 с помощью модификатора max 6 Разложение в ряд Тейлора С помощью символьного процессора Mathcad возможно получить разложение выражения в ряд Тейлора по любой переменной х в точке х = 0. Чтобы разложить выражение в ряд необходимо: Ввести выражение. Выделить значение переменной, по которой требуется получить разложение в ряд. Выполнить команду Symbolics / Variable / Expand to Series. В появившемся диалоговом окне ввести желаемый порядок аппроксимации (Order of Approximation) и нажать кнопку ОК. Пример 10. Разложим в ряд Тейлора функцию №1381 из книги «Сборник задач и упражнений по математическому анализу» (рисунок 12). 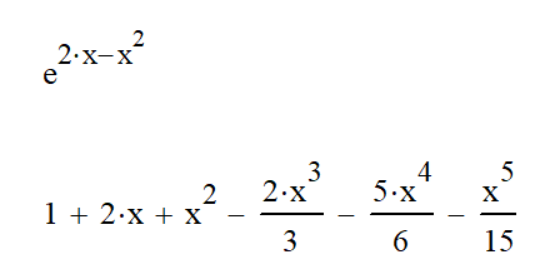 Рисунок 12 - Разложение в ряд Тейлора функции №1381 Пример 11. Разложим в ряд Тейлора функцию №1384 из книги «Сборник задач и упражнений по математическому анализу» (рисунок 13). 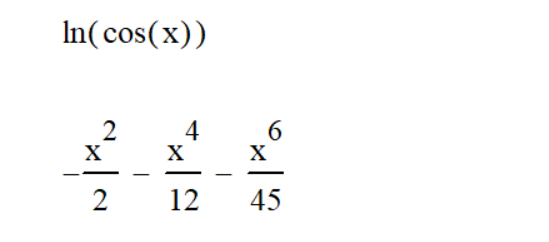 Рисунок 13 - Разложение в ряд Тейлора функции №1384 Стоит не забывать, что разложение строится только в точке х=0. Чтобы получить разложение в другой точке х=а, можно, к примеру, подставить вместо переменной х значение х-а. Для разложения в ряд альтернативным способом, с помощью оператора символьного вывода, используется ключевое слово series, вставляемое одноименной кнопкой панели Symbolic. После ключевого слова series, через запятую, указывается имя переменной, по которой производится разложение, и порядок аппроксимации. Пример 12. Разложим в ряд Тейлора функцию №1384 из книги «Сборник задач и упражнений по математическому анализу» с помощью ключевого слова series (рисунок 14). 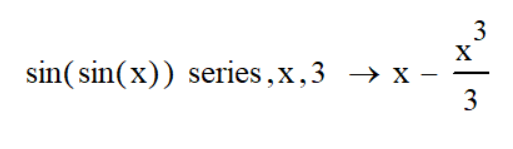 Рисунок 14 - Разложение в ряд Тейлора функции №1384 с помощью ключевого слова series Пример 13. Разложим в ряд Тейлора функцию №1387 из книги «Сборник задач и упражнений по математическому анализу» с помощью ключевого слова series (рисунок 15). 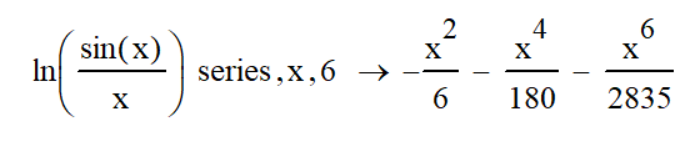 Рисунок 15 - Разложение в ряд Тейлора функции №1387 с помощью ключевого слова series ЗАКЛЮЧЕНИЕ В ходе данной работы с помощью пакета Mathcad было изучено способы решения задач по таким темам как вычисление пределов функций, вычисление производной, вычисление интегралов, нахождение нулей полинома, упрощение выражений и разложение в ряд Тейлора. СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ Богомолова, Е.П. Решатели или великолепная семерка Mathcad / Е.П. Богомолова, В.Ф. Очков, М. Хейнлоо // Открытое образование. – 2015. – №3. – С. 37-50. Воскобойников Ю.Е. Основы вычислений и программирования в пакете MathCAD: учеб. пособие/Ю.Е.Воскобойников[и др.]; под ред. Ю. Е.Воскобойникова; Новосиб. гос. архитектур.-строит. ун-т (Сибстрин). –Новосибирск: НГАСУ(Сибстрин), 2012. –212с. Демидович Б. П. Сборник задач и упражнений по математическому анализу./Спб: Мифрил. 1995. -489с.Кирьянов Д. Самоучитель Mathcad 13; Книга по Требованию - Москва, 2006. - 521 c. Кирьянов Д. Самоучитель Mathcad 11; Книга по Требованию - Москва, 2012. - 544 c.Новиковский Е.А. Учебное пособие «Работа в системе MathCAD» /Е.А.Новиковский.–Барнаул: Типография АлтГТУ, 2013.–114с.Сканави М.И. Сборник конкурсных задач по математике для поступающих во втузы 3-е изд., доп. — М.: Высшая школа, 1978. — 519с. | ||||||||||||||||||||||||||||||||||||||||||||||||||
