УТП 2 ЛАБА. лаба 2. N. 4 на интервале a,b. Сделайте вывод о влиянии числа членов разложения на точность аппроксимации
 Скачать 420.78 Kb. Скачать 420.78 Kb.
|
|
Вариант 17 Задание 2.1. Найти разложения Тейлора заданной функции f x (табл. 6.1) в точке x0 при числе слагаемых n от 1 до 4 с помощью приложения taylortool и функции taylor. Построить графики исходной функции, ряда Тейлора и ошибки аппроксимации при n=1..4 на интервале a,b . Сделайте вывод о влиянии числа членов разложения на точность аппроксимации. >> syms x t=0:0.001:4; f=cos(x); G=[ ]; for n=1:4 p=taylor(cos(x),x,1,'order',n); g=subs(p,t); plot(t,g,'MarkerSize',2,'LineWidth',2) grid on hold on xlabel('t') G=[G;p] end G =cos(1) G = cos(1) cos(1) - sin(1)*(x - 1) G = cos(1) cos(1) - sin(1)*(x - 1) cos(1) - sin(1)*(x - 1) - (cos(1)*(x - 1)^2)/2 G = cos(1) cos(1) - sin(1)*(x - 1) cos(1) - sin(1)*(x - 1) - (cos(1)*(x - 1)^2)/2 cos(1) + (sin(1)*(x - 1)^3)/6 - sin(1)*(x - 1) - (cos(1)*(x - 1)^2)/2 >> legend('cos(x)','g(x,1)-разложение на 1 член','g(x,2)-разложение на 2 члена','g(x,3)- разложение на 3 члена','g(x,4)-разложение на 4 члена') 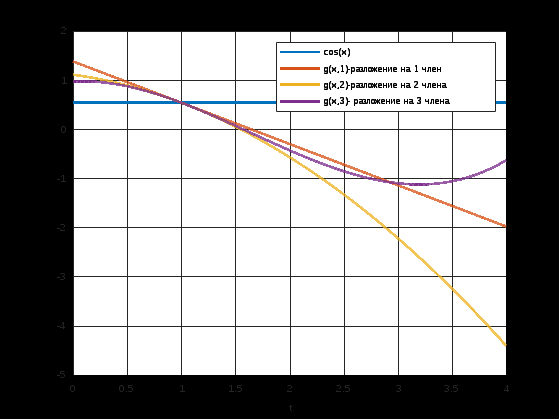 Рисунок 1.Графики функции y=exp(x) и ее разложение в ряд Тейлора. syms x t=0:0.001:4; f=cos(t+1); plot(t,f,'k','MarkerSize',2,'LineWidth',2) hold on for n=1:4 p=taylor(cos(x),x,1,'order',n); g=subs(p,t); och=f-g plot(t,och,'--','MarkerSize',2,'LineWidth',2) grid on xlabel('t') end legend('cos(x)','ошибка апроксимаци при n=4','ошибка апроксимации при n=3','ошибка апроксимации при n=2 ','ошибка апроксимации при n=1') 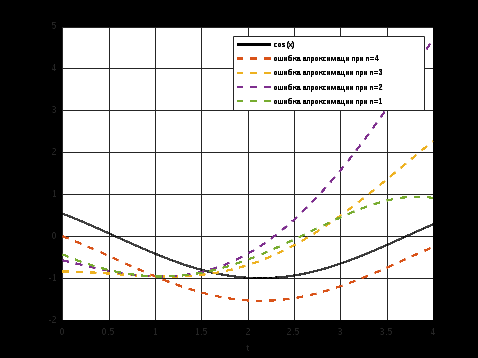 Рисунок 2. Графики функции y=cos(x) и ошибки аппроксимации. 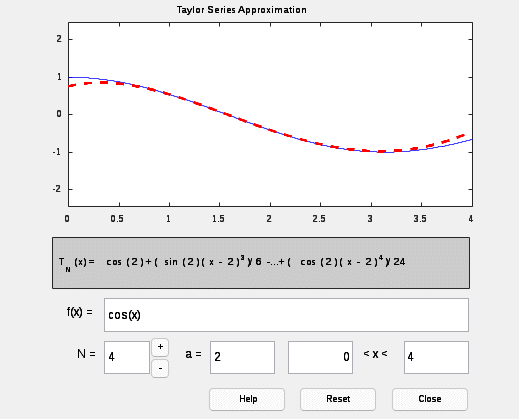 Рисунок. 3 График функции y=cos(x) и ее аппроксимации с разложением на 4 члена ряда 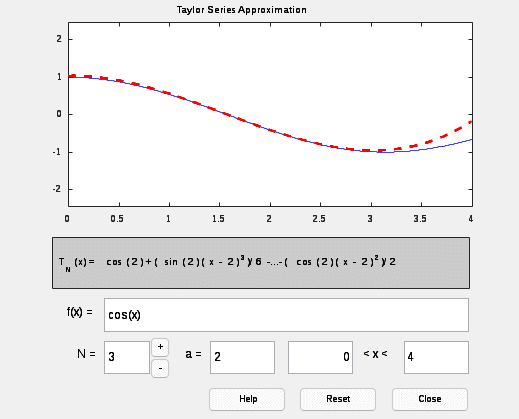 Рисунок. 4 График функции y=cos(x) и ее аппроксимации с разложением на 3 члена ряда 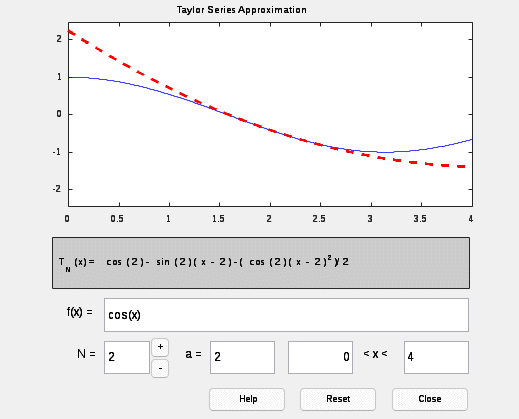 Рисунок. 5 График функции y=cos(x) и ее аппроксимации с разложением на 2 члена ряда 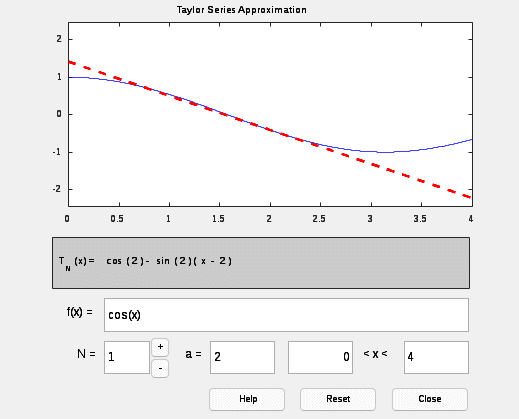 Рисунок. 6 График функции y=cos(x) и ее аппроксимации с разложением на 1 члена ряда Вывод: С увеличением числа членов разложения ряда Тейлора растет точность аппроксимации Рассматриваемая аппроксимация описывает заданную функцию наиболее точно при значениях х, близких к x0, и менее точно при значениях х, значительно отличающихся от х0. |
