математика. 6,7,8 мат. Вид ресурсов
 Скачать 65.04 Kb. Скачать 65.04 Kb.
|
|
Задание № 6 Оптимальное планирование. Постановка задачи: предприятие располагает ресурсами сырья, рабочей силы и оборудованием, необходимым для производства любого из трех видов производимых товаров 1, 2, 3. Затраты ресурсов на изготовление единицы товара, а также запасы ресурсов указаны в следующей таблице: Таблица 1
Определить какой ассортимент товара надо выпускать, чтобы прибыль была максимальной, используя следующие данные: 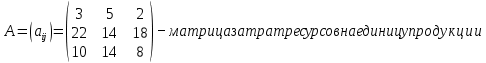 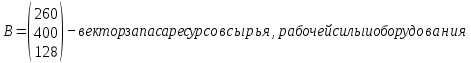 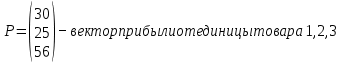 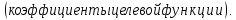 Информацию представить в виде таблицы №1, построить модель. Решить симплексным методом, проанализировать полученный результат. Решение. Исходную информацию представим в виде таблицы №1: Таблица 1
Обозначим х1, х2, х3 – число единиц продукции вида 1, 2 и 3 соответственно, запланированных к производству. Для их изготовления потребуется (3х1 + 5х2 + 2х3) кг. сырья, (22х1 + 14х2 + 18х3) ч. рабочей силы, (10х1 + 14х2 + 8х3) станко-час. оборудования. Потребление ресурсов не должно превышать их запасов, соответственно 260, 400 и 128 единиц. Тогда экономико-математическую модель задачи можно сформулировать так: Найти план выпуска продукции Х = (х1, х2, х3), удовлетворяющий системе ограничений: 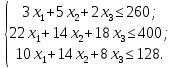 и условию х1, х2, х3 ≥ 0, при котором функция F = 30х1 + 25х2 + 56х3 принимает максимальное значение. Решим прямую задачу линейного программирования симплексным методом, с использованием симплексной таблицы. Для построения первого опорного плана систему неравенств приведем к системе уравнений путем введения дополнительных переменных (переход к канонической форме). В 1-м неравенстве смысла (≤) вводим базисную переменную x4. В 2-м неравенстве смысла (≤) вводим базисную переменную x5. В 3-м неравенстве смысла (≤) вводим базисную переменную x6. 3x1 + 5x2 + 2x3 + x4 = 260 22x1 + 14x2 + 18x3 + x5 = 400 10x1 + 14x2 + 8x3 + x6 = 128 Матрица коэффициентов A = a(ij) этой системы уравнений имеет вид: 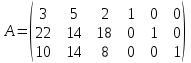 Решим систему уравнений относительно базисных переменных: x4, x5, x6. Полагая, что свободные переменные равны 0, получим первый опорный план: X0 = (0, 0, 0, 260, 400, 128).
Текущий опорный план не оптимален, так как в индексной строке находятся отрицательные коэффициенты. В качестве ведущего выберем столбец, соответствующий переменной x3, так как это наибольший коэффициент по модулю. Вычислим значения Di по строкам как частное от деления: bi/ai3 и из них выберем наименьшее: min (260:2, 400:18, 128:8) = 16. Следовательно, 3-ая строка является ведущей. Разрешающий элемент равен (8) и находится на пересечении ведущего столбца и ведущей строки.
Пересчитаем симплекс-таблицу по правилу прямоугольника. Получаем новую симплекс-таблицу:
Среди значений индексной строки нет отрицательных. Поэтому эта таблица определяет оптимальный план задачи, который можно записать так: x1 = 0, x2 = 0, x3 = 16. F(X) = 30·0 + 25·0 + 56·16 = 896. Анализ оптимального плана. В оптимальный план вошла дополнительная переменная x4. Следовательно, при реализации такого плана имеются недоиспользованные ресурсы 1-го вида в количестве 228. В оптимальный план вошла дополнительная переменная x5. Следовательно, при реализации такого плана имеются недоиспользованные ресурсы 2-го вида в количестве 112. Значение 40> 0 в столбце x1 означает, что использование x1 - не выгодно. Значение 73> 0 в столбце x2 означает, что использование x2 - не выгодно. Значение 0 в столбце x3 означает, что использование x3 - выгодно. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
