математика. 6,7,8 мат. Вид ресурсов
 Скачать 65.04 Kb. Скачать 65.04 Kb.
|
|
Задание № 7 Графический метод. Постановка задачи: для изготовления двух видов продукции имеются три вида ресурсов, объемы которых ограничены величинами b1, b2, b3 соответственно. Расход i-го вида ресурса на изготовление одной единицы j-го вида продукции равен aij, i = 1, 2, 3, j = 1, 2. Объем выпуска каждого из видов продукции ограничен число x1* и x2* единиц, прибыль, получаемая от реализации одной единицы изготовленной продукции равна с1 и с2 соответственно. Данные задачи могут быть представлены в форме таблицы:
Требуется составить план выпуска продукции (число единиц продукции по каждому виду), удовлетворяющий принятым ограничениям и приносящий максимум прибыли после реализации выпущенной продукции, имея следующие данные: 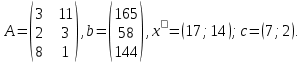 Решение. Исходные данные:
Математическая модель задачи: Обозначим х1, х2 – число единиц продукции вида 1 и 2, запланированных к производству. Для их изготовления потребуется (3х1 + 11х2) единиц ресурса 1, (2х1 + 3х2) единиц ресурса 2, (8х1 + х2) единиц ресурса 3. Потребление ресурсов не должно превышать их запасов, соответственно 165, 58 и 144 единиц. Объем выпуска каждого из видов продукции ограничен 17 и 14 единиц соответственно. Тогда экономико-математическую модель задачи можно сформулировать так: Найти план выпуска продукции Х = (х1, х2), удовлетворяющий системе ограничений: 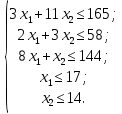 и условию х1, х2 ≥ 0, при котором функция F = 7х1 + 2х2= 0 принимает максимальное значение. Для графического решения задачи построим множество допустимых решений, задаваемое неравенствами-ограничениями (1) – (5): 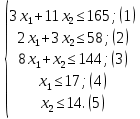 Ограничение (1) в задаче определяется прямой 3x1 + 11x2 = 165, проходящей через точки:
Множество допустимых решений в задаче будет ограничено этой прямой, и будет содержать точку (0, 0)Т, так как при подстановке координат этой точки в ограничение (1) получается верное неравенство: 3·0 + 11·0 ≤ 165. Ограничение (2) в задаче определяется прямой 2x1 + 3x2 = 58, проходящей через точки:
Множество допустимых решений в задаче будет ограничено этой прямой и будет содержать точку (0, 0)Т, так как при подстановке координат этой точки в ограничение (2) получается верное неравенство: 2·0 + 3·0 ≤ 58. Ограничение (3) в задаче определяется прямой 8x1 + x2 = 144, проходящей через точки:
Множество допустимых решений в задаче будет ограничено этой прямой, и будет содержать точку (0, 0)Т, так как при подстановке координат этой точки в ограничение (3) получается верное неравенство: 8·0 + 0 ≤ 144. Ограничение (4) в задаче определяется прямой x1 = 17, параллельной оси х2. Множество допустимых решений в задаче будет ограничено этой прямой, и будет содержать точку (0, 0)Т, так как при подстановке координат этой точки в ограничение (3) получается верное неравенство: 0 ≤ 17. Ограничение (5) в задаче определяется прямой x2 = 14, параллельной оси х1. Множество допустимых решений в задаче будет ограничено этой прямой, и будет содержать точку (0, 0)Т, так как при подстановке координат этой точки в ограничение (3) получается верное неравенство: 0 ≤ 14. Ограничения х1 ≥ 0, х2 ≥ 0 в задаче задают 1-ю четверть координатной плоскости. Множество допустимых решений включает все точки, в которых ограничения выполняются одновременно. Отметим крайние точки получившегося множества: A, B, С, D, E.  Построим градиент функции f (X) = (7, 2)Т в точке (0, 0)Т. Построим линию уровня функции f (X) = C , проходящую через точку (0, 0)Т. Для этого найдем значение константы C , подставив координаты точки в целевую функцию: C = 7· 0 + 2· 0 = 0, и затем построим прямую 7x1 + 2x2 =0. Построенная линия уровня перпендикулярна градиенту и пересекает множество допустимых решений. Вектор-градиент, составленный из коэффициентов целевой функции, указывает направление максимизации f(X). Будем двигать эту прямую параллельным образом. Поскольку нас интересует наибольшее значение f(x), поэтому двигаем прямую до последнего касания обозначенной области. Прямая F(x) = const пересекает область в точке D. Так как точка D получена в результате пересечения прямых (3) и (4), то ее координаты удовлетворяют уравнениям этих прямых:  Решив систему уравнений, получим: x1 = 17; x2 = 8. Откуда найдем максимальное значение целевой функции: Fmax (X) = 7·17 + 2·8 = 135. Задание № 8 Транспортная задача. Постановка задачи: на складах А1, А2, А3 имеются запасы продукции в количествах 180, 300, 120 т. соответственно. Потребители В1, В2, В3 должны получить эту продукцию в количествах 110, 350, 140 т. соответственно. Найти такой вариант прикрепления поставщиков к потребителям, при котором сумма затрат на перевозки была бы минимальной. Расходы по перевозке 1 т. продукции заданы матрицей С (ден.ед.) 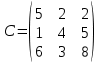 Решение. Стоимость доставки единицы груза из каждого пункта отправления в соответствующие пункты назначения задана матрицей тарифов:
Проверим необходимое и достаточное условие разрешимости задачи. ∑a = 180 + 300 + 120 = 600 ∑b = 110 + 350 + 140 = 600 Условие баланса соблюдается. Запасы равны потребностям. Следовательно, модель транспортной задачи является закрытой. Используя метод наименьшей стоимости, построим первый опорный план транспортной задачи. Искомый элемент равен c21 = 1. Для этого элемента запасы равны 300, потребности 110. Поскольку минимальным является 110, то вычитаем его. x21 = min(300, 110) = 110.
Искомый элемент равен c12 = 2. Для этого элемента запасы равны 180, потребности 350. Поскольку минимальным является 180, то вычитаем его. x12 = min(180, 350) = 180.
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
