Методы оптимизации, лаб.работа №7. Методы оптимизации, лаб. работа №7. Лабораторная работа 7. Вариант Алгоритм графического метода решения злп
 Скачать 129.06 Kb. Скачать 129.06 Kb.
|
|
Лабораторная работа №7. Вариант 5. 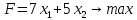 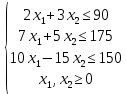 Алгоритм графического метода решения ЗЛП Для того чтобы решить графически ЗЛП необходимо выполнить следующие действия. 1. Построить множество допустимых планов задачи. В общем случае оно представляет собой выпуклый многогранник. Если ограничения в задаче несовместны, множество допустимых планов является пустым множеством, а задача поиска экстремума не имеет смысла. 2. Построить вектор С, с началом в некоторой точке 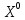 3. Построить гиперплоскость линейной формы (линию уровня) проходящую через точку 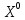 4. Передвигать гиперплоскость линейной формы параллельно самой себе в направлении вектора C (так как вектор 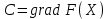 задает направление возрастания F(X)) до получения опорной гиперплоскости. задает направление возрастания F(X)) до получения опорной гиперплоскости.Постановка задачи Для начала мы обозначим условия ограничений. В нашем случае их три 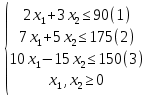 Теперь рассмотрим ограничения по порядку. Если заменить неравенство на знак “=”, то получится уравнение прямой. В таком случае найдём по две точки для каждого неравенства. 1)
2)
3)
Далее строим прямые и обозначаем ограничения, тем самым выстраивается многоугольник  Далее необходимо построить вектор 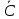 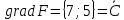  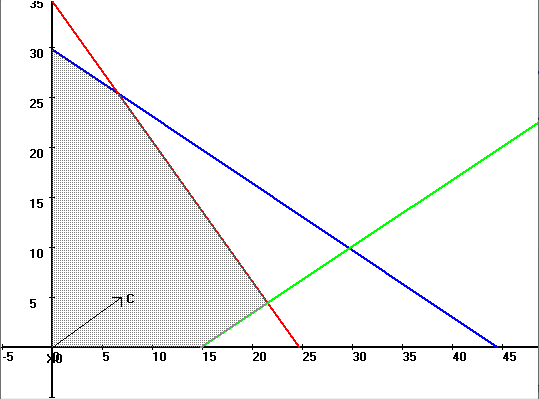 Далее необходимо задать линию уровня. 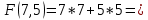 74 74Получится уравнение линии:  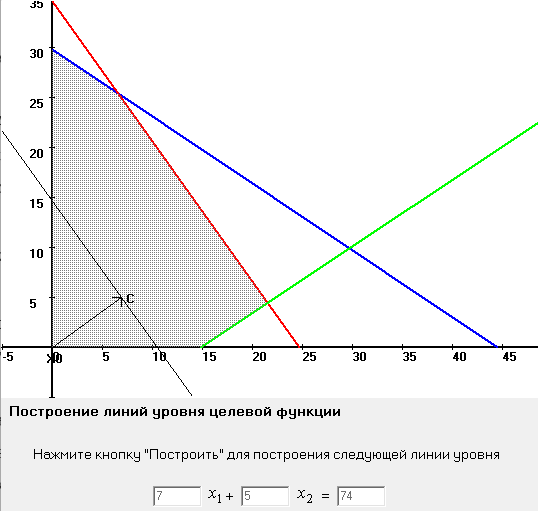 Далее строим следующие линии уровня, параллельные начальной 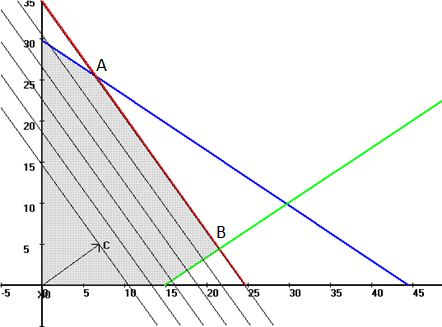 Из полученного графика мы уже можем сделать вывод, что задача по итогу имеет бесконечное множество решений, т.к. линия уровня полностью параллельна одной из граней многогранника. В таком случае нам нужно найти координаты нижней и верхней точек. Для того чтобы их найти, необходимо решить системы уравнений. Точка A: 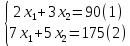 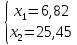 A (6,82 ; 25,45) A (6,82 ; 25,45)Точка B: 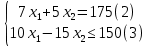  B (21,77 ; 4,52) B (21,77 ; 4,52)Далее находим  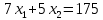  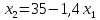   И наконец находим 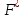  - по точке B - по точке B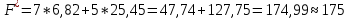 - по точке A - по точке A Задача решена. |
