Пример графического метода решения задачи линейного программиров. 1. Поиск оптимального решения графического метода lpm
 Скачать 74.92 Kb.
|
|
Пример графического метода решения задачи линейного программирования. 1.Поиск оптимального решения графического метода LPM. Поскольку модель, обсуждаемая в теме 1, содержит только две переменные, проблема может быть решена графически. В случае трех переменных графическое решение становится менее визуальным, а при большем количестве омелы оно становится невозможным вообще. Несмотря на это, рассмотрение графического метода позволит сделать выводы, которые послужат основой для разработки общего метода решения задач ЛП. Первым шагом при использовании графического метода является представление области приемлемых решений, в которой одновременно удовлетворяются все ограничения модели. Желаемая площадь (пространство) решений задачи примера 1.1. показано на рисунке 2. 2.1. Условия неотчуждаемости переменных ограничивают площадь их допустимых значений первым квадрантом координатной плоскости (часть плоскости над осью х1 и справа от оси х2). Другие границы пространства решений изображаются прямыми линиями, построенными на уравнениях, полученных путем замены знака «£» знаком «=» в ограничениях. Области, в которых соответствующие ограничения выполняются как неравенства (в нашем случае неравенства со знаком «<»), обозначаются стрелками, направленными в сторону допустимых значений переменных. Результирующим пространством для решения задачи красок является многоугольник ABCDЕF (рис. 2.1). В каждой точке, относящейся к внутренней области или границам полигона решения ABCDEF, выполняются все ограничения, поэтому решения, соответствующие этим точкам, допустимы. Среди бесконечного числа таких точек можно найти точку оптимального решения, если выяснить, в каком направлении растет целевая функция. 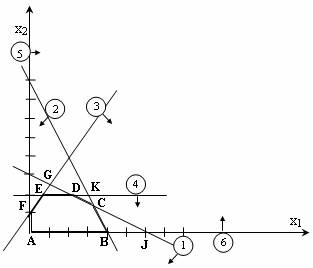 Рис. 2.1. Пространство допустимых решений задачи «о красках». На рисунке 2. 2.2 Показывает, как выполняется такая операция. На рисунке 2. 2.2 Показывает, как выполняется такая операция. 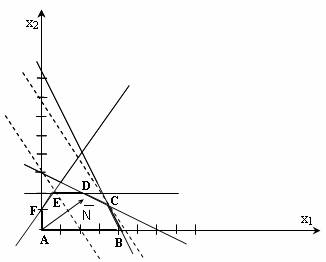 Рис. 2.2. Поиск оптимального решения THELP графическим методом. График применяется к линии уровня целевой функции c1×x1+c2×x2=z0, где z0 — произвольное значение z. Построить вектор N (c1, c2), который является нормальным для линий уровня целевой функции и определяет направление оптимизации z. Последняя точка в этой области будет оптимальной точкой. Очевидно, что оптимальное решение соответствует точке С-точки пересечения линий (1) и (2). Значения x1 и x2 в точке C определяются решением системы уравнений:  Решение этой системы x1=3  ; x2 = 1 . Полученная в этом случае прибыль составит: z=3x1+2x2 =3×3 +2×1 =12 (тыс. г.о.)Заметим, что в случае, когда линии уровня z имеют тот же наклон, что и линия ограничения привязки (то есть проходящие через оптимальную точку), у нас будет много оптимумов на отрезке. 2. Анализ ZLP-моделей по чувствительности: цель и задачи. После получения оптимального решения задачи ЛП часто возникает необходимость выявить чувствительность этого решения к определенным изменениям параметров исходной модели. Например, проблема красок может представлять интерес для вопроса о том, как оптимальное решение повлияет на увеличение или снижение спроса, изменение запасов ресурсов, а также рыночных цен на товары. При таком анализе всегда рассматривается определенный набор линейных оптимизационных моделей, что придает модели динамизм, присущий реальным процессам. Отсутствие методов обнаружения влияния возможных изменений параметров модели на оптимальное решение может привести к тому, что результирующее (статическое) решение устареет еще до его реализации. В рамках анализа на чувствительность решения, полученного графическим методом, решаются следующие три задачи: 1) анализ чувствительности к изменениям в правой части ограничений; 2) анализ степени дефицита ресурсов; 3) анализ решения ЗЛП по чувствительности к изменениям коэффициентов целевой функции. 3. Первая задача анализа чувствительности: анализ чувствительности к изменениям в правых частях ограничений. Эта задача позволяет ответить на вопрос: насколько целесообразно увеличивать или уменьшать ресурсные запасы? Особенно важно проанализировать эти два аспекта. 1. На какое значение можно увеличить запас какого-либо ресурса для повышения оптимального значения целевой функции? 2. На какое значение можно уменьшить запас какого-либо ресурса при сохранении оптимального значения целевой функции? Поскольку объем запаса каждого из ресурсов фиксируется в нужных частях ограничений, этот вид анализа часто называют анализом назойливости нужных частей (ограничений). Прежде чем ответить на поставленные вопросы, мы классифицируем ограничения линейной модели на связующие (активные) и несвязывающие (неактивные). Линия, соответствующая пределу привязки, должна проходить через оптимальную точку. На рисунке 2. 2.1 Привязками являются только ограничения (1) и (2), то есть те, которые ограничивают запасы ресурсов А и В. Если какое-то ограничение является обязательным, то ресурс, который ему соответствует, следует отнести к разрядке дефицитных ресурсов, так как он расходуется полностью. Ресурс, с которым связан необязательный лимит, следует отнести к категории недефицитных ресурсов (то есть имеющихся в некотором избытке). Таким образом, в ходе анализа модели на чувствительность к правым частям ограничений определяются следующие значения: 1) предельно допустимое увеличение запаса дефицитного ресурса, позволяющего улучшить ранее найденное оптимальное решение; 2) предельно допустимое уменьшение запаса недефицитного ресурса, не изменяющего ранее найденного значения целевой функции. Информация, полученная в последнем случае, особенно полезна в ситуациях, когда избыточные недефицитные ресурсы могут быть использованы для других целей. Может возникнуть вопрос: не стоит ли анализировать, как увеличение количества ресурсов, которые находятся в избытке, и уменьшение количества дефицитных ресурсов повлияет на оптимум. Ответ на первую часть вопроса очевиден, ведь в этом случае мы постараемся сделать и без того избыточный ресурс еще более избыточным, что не повлияет на ранее полученное решение. Вторая часть вопроса заслуживает особого внимания, так как при возможных недопоставках дефицитного ресурса важно знать, как это отразится на результатах решения проблемы. Вернемся к конкретному примеру. В проблеме «на красках» продукты А и В (ограничения (1) и (2)) являются дефицитными ресурсами. Рассмотрим сначала ресурс А. На рис. 1. 2.3 Видно, что при увеличении запаса этого ресурса линия (1) (или отрезок D) движется вверх параллельно себе, постепенно «подтягивая» треугольник СD к точке. Стороны CK и DK этого треугольника представляют собой продолжение линий, соответствующих границам (2) и (4). В точке K ограничения (2) и (4) становятся обязательными; оптимальное решение соответствует точке К, а пространственным (допустимым) решением является многоугольник AVKEF. В точке K предел (1) (для ресурса A) становится избыточным, так как любое дальнейшее увеличение запаса соответствующего ресурса не повлияет ни на пространство решения, ни на оптимальное решение. Таким образом, объем ресурса А не следует увеличивать до высоты предела, соответствующего точке, в которой предел (1) становится избыточным. 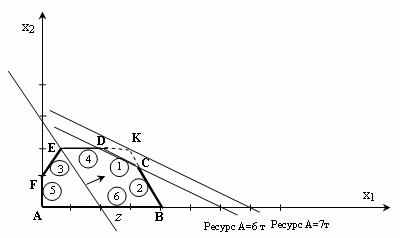 Рис. 2.3. Определение предельно допустимого прироста запаса ресурса А. Этот предельный уровень определяется следующим образом. Во-первых, устанавливаются координаты точки, в которой пересекаются прямые (2) и (4), то есть происходит решение системы уравнений:  В результате получается x1=3 и x2=2. Подставляя координаты точки К в левую сторону ограничения (1), определяем максимально допустимый запас ресурса А: x1+2 x2=2=3+2× 2=7 t. Рис. 2.4 иллюстрирует ситуацию, когда рассматривается вопрос о целесообразности увеличения запаса дефицитного ресурса (2) (исходный продукт В). Новой оптимальной точкой является точка J, где пересекаются линии (6) и (1), то есть x2 = 0, x1 + 2x2 = 6. Отсюда следует, что x1=6,x2=0, а запас продукта B может быть увеличен до значения, равного 2x1+x2=2×6+1×0=12 t. 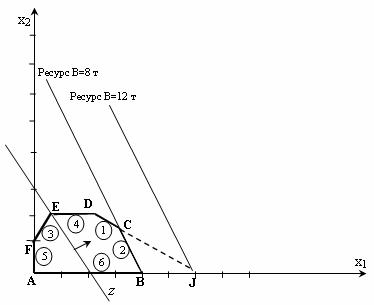 Рис. 2.4. Визначення максимально допустимого збільшення запасу ресурсу В. Розглянемо тепер питання про зменшення правої частини незв’язуючих обмежень. Обмеження (4), x2  2 фіксує граничний рівень попиту на фарбу другого виду. На рис. 2.2. видно, що, не змінюючи оптимального розв’язку, пряму (4) (ЕD) можна опускати донизу до перетину з оптимальною точкою С. Оскільки точка С має координати x1 = і x2= то, зниження попиту на фарбу 2 до величини x2= ніяк не вплине на оптимальність раніше отриманого розв’язку.Розглянемо обмеження (3), -x1+ x2 1, що описує співвідношення між попитом на фарбу 2 і попитом на фарбу 1. У цьому випадку праву частину обмеження можна зменшувати доти, поки пряма (3) (ЕF) не досягне точки С, При цьому права частина обмеження (3) стане рівною -x1+ x2=(- )+( )= -2, що дозволяє записати це обмеження у вигляді: -x1+ x2 -2, або в еквівалентній формі: x1- x2 . Цей результат показує, що раніше отриманий оптимальний розв’язок не зміниться, якщо попит на фарбу 1 перевищить попит на фарбу 2 не більше, ніж на 2 т.Результати проведеного аналізу можна звести в таку таблицю. Таблиця 2.1
4. Друга задача аналізу на чутливість: оцінка дефіцитності ресурсів. За допомогою методів лінійного програмування вдається відповісти на запитання: збільшення обсягу якого з ресурсів є найбільш вигідним? Для цього вводиться характеристика цінності кожної додаткової одиниці дефіцитного ресурсу, що виражається через відповідне збільшення оптимального значення цільової функції. Таку характеристику для аналізованого прикладу можна одержати безпосередньо з таблиці з результатами розв’язання першої задачі аналізу на чутливість. Позначимо цінність додаткової одиниці ресурсу i через yi . Величину yi визначимо із співвідношення:  де Dbі – приріст запасу і-го ресурсу, Dz i - приріст цільової функції, зумовлений збільшенням і-го ресурсу на величину Dbі. Скориставшись даними зазначеної таблиці, для обмеження (1) (продукт А), одержимо  тис. г.о./ т продукту А.Аналогічно визначається цінність одиниці будь-якого іншого ресурсу (результати розрахунку представлені в табл. 2.2. Значення величин yi свідчать про те, що додаткові вкладення в першу чергу варто направити на збільшення запасу ресурсу 2 (продукт В) і лише потім - на збільшення ресурсу 1 (продукт А). Щодо недефіцитних ресурсів, то їхній обсяг, як і слід було очікувати, збільшувати недоцільно. Таблиця 2.2.
2.5. Третя задача аналізу на чутливість: аналіз на чутливість до зміни коефіцієнтів цільової функції. Дозволяє відповісти на запитання: в яких межах є допустимою зміна коефіцієнтів цільової функції? Зміна коефіцієнтів цільової функції впливає на нахил прямої, що описує цю функцію в прийнятій системі координат. Раніше було показано, що ідентифікація конкретної кутової точки в якості оптимуму залежить насамперед від нахилу цієї прямої. Це означає, що варіація коефіцієнтів цільової функції може призвести до зміни сукупності зв’зуючих обмежень і, отже, статусу того чи іншого ресурсу (тобто зробити недефіцитний ресурс дефіцитним і навпаки). Таким чином, у рамках аналізу моделі на чутливість до змін коефіцієнтів цільової функції можуть досліджуватися такі питання: 1. Яким є діапазон зміни (збільшення або зменшення) того або іншого коефіцієнта цільової функції, при якому не відбувається зміни оптимального розв’язку? 2. Наскільки варто змінити той або інший коефіцієнт цільової функції, щоб зробити деякий недефіцитний ресурс дефіцитним і, навпаки, дефіцитний ресурс зробити недефіцитним? Обговоримо поставлені питання на прикладі задачі «про фарби». Розглядаючи перше питання, позначимо через C1 і С2 прибутки фірми від продажу 1 т відповідно фарби 1 і фарби 2. Тоді цільову функцію можна подати в такому вигляді: Z=C1x1+C2x2. На рис. 2.5 видно, що при збільшенні C1 або зменшенні C2 пряма, що описує цільову функцію , обертається (навколо точки С) за годинниковою стрілкою. Якщо ж C1 зменшується або C2 збільшується, ця пряма обертається проти годинникової стрілки. Таким чином, точка С буде залишатися оптимальною точкою доти, поки нахил прямої не вийде за межі, обумовлені нахилами прямі для обмежень (1) і (2). 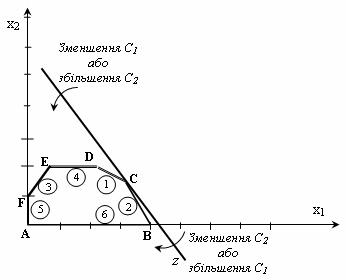 Рис. 2.5. Определение предельных значений коэффициентов целевой функции. Как только наклон линии Z станет равен наклону прямого предела (1), мы получим альтернативные оптимальные угловые точки C и D. Аналогично, если наклон линии Z станет равен наклону линии для предела (2), мы получим две альтернативные оптимальные угловые точки B и C. (Наличие альтернативных оптимумов указывает на то, что одно и то же оптимальное значение Z может быть достигнуто при разных значениях переменных. одержим каким-то новым оптимальным решением (точка B или точка D). Чтобы проиллюстрировать эту процедуру расчета, рассмотрим, как можно найти допустимый интервал изменения С1, в какой точке С остается оптимальным. Начальное значение коэффициента С2 =2 остается неизменным. Из риса. 2.5 показывает, что значение C1 может быть увеличено до тех пор, пока линия Z не совпадет с линией (2), или уменьшаться до тех пор, пока линия Z не совпадет с линией (1). Эти предельные значения коэффициента С1 могут быть определены из равенства наклонов линии Z и линии (2) (максимальное значение С1) и равенства наклонов линии Z и линии (1) (минимальное значение). Поскольку тангенс угла наклона для линии Z равен C1/2, а для линий (1) и (2) соответственно 1/2 и 2/1, минимальное значение C1 определяется из равенства: C1=1/2, откуда C1 min =1, и максимум равенства: C1/2=2/1, C1 max=4. Интервал изменения C1, в котором точка C по-прежнему является единственной оптимальной точкой, определяется неравенством £1 C1 £4. При С1=1 оптимальными угловыми точками будут В и С. Как только коэффициент С1 становится меньше 1, оптимальный сдвигается в точку D. Аналогичная интерпретация может быть дана в случае, когда коэффициент С1 ³4. Можно отметить, что как только C1 меньше 1, ресурс 2 становится неэффективным, а ресурс 4 становится дефицитным. Такой же анализ можно провести для коэффициента С2, при фиксации С1 на уровне С1 = 3 тыс. рублей. г.о./т. Теперь представим, что коэффициенты целевой функции совпадают с соответствующими коэффициентами одного из связывающих ограничений или пропорциональны им. Например, пусть общая прибыль компании будет описана в задаче чернил функцией z = 4x1 +2x2 . В этом случае линии целевого уровня функции будут параллельны прямому пределу (2). Таким образом, оптимальное решение будет соответствовать бесконечному множеству точек, принадлежащих сегменту VC. Резюме: 1. Графический метод решения PLR эффективен только с двумя переменными и в целом возможен - с количеством переменных не более трех. 2. Анализ модели на чувствительность является обязательным этапом решения любой задачи оптимизации, необходимой для разработки информированных решений в постоянно меняющихся условиях. |
=+
